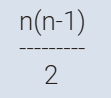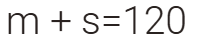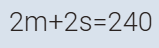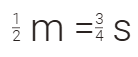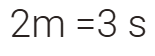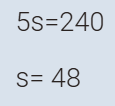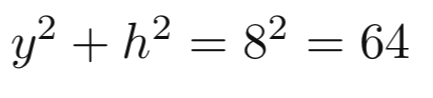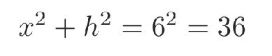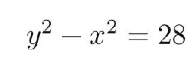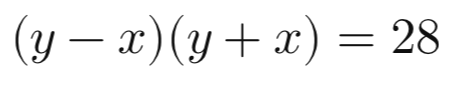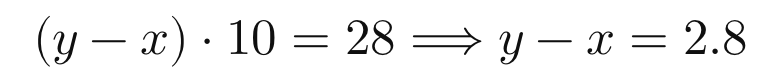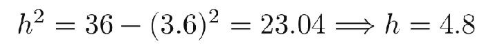
شكر وتقدير
كل الشكر والتقدير لجامعة الملك سعود والشكر موصول
للجمعية السعودية للعلوم التربوية والنفسية
ومركز التميز البحثي في تطوير
تعليم العلوم والرياضيات
شكر وتقدير
كل الشكر والتقدير للسيدات والسادة
الحضور
رابط اللقاء

STRAT
-
استراتيجية التخمين والتحقق (Guess
and Check)
- استراتيجية
بناء جدول (Make a Table)
- استراتيجية البحث عن نمط (Look for
a Pattern)
-
استراتيجية البدء من
النهاية (Work Backward)
- استراتيجية
التمثيل البصري
(Visual Representation )
-
استراتيجية كتابة معادلة (Write an
Equation)
- استراتيجية
التبسيط (Simplify the Problem)
-
استراتيجية النمذجة الرياضية (
Mathematical Modeling )
-
استراتيجية التجربة المنظمة
(Systematic Listing)
-
استراتيجية تطبيق قاعدة أو قانون ( قانون المتتاليات )
استراتيجيات
حل المشكلات
استراتيجية التخمين والتحقق
(Guess and Check)
حل المشكلة بالتخمين المبدئي لقيمة المجهول ثم التحقق مما إذا
كانت تحقق شروط المشكلة، وتكرار العملية
حتى الوصول للحل الصحيح
استراتيجية
البحث عن نمط
(Look for a Pattern)
حل المشكلة عن طريق ملاحظة(اكتشاف)
نمط أو تسلسل بين القيم
لتحديد الحل
أو التنبؤ بالقيم المستقبلية
استراتيجية كتابة معادلة
(Write an Equation)
تحويل (ترجمة) صياغة المشكلة إلى
معادلة واحدة ( ليست قانون
عام ) تمثل العلاقة بين الأعداد والمجهول، ليتم حلها مباشرة.
استراتيجية
بناء جدول
(Table Strategy)
تنظيم البيانات والمعلومات في جدول مرتب لتوضيح العلاقات بين
الكميات والمساهمة في رؤية النمط أو الحل بطريقة منظمة.
استراتيجية التمثيل البصري
(Visual Representation )
تمثيل المشكلة باستخدام رسوم، أشكال ، أو أي تمثيل بصري لتوضيح
العلاقات بين الكميات مما يسهل فهم المشكلة والوصول للحل .
استراتيجية البدء من النهاية
(Working
Backwards)
حل المشكلة بالبدء من النتيجة النهائية، ثم
الرجوع خطوة خطوة
للخلف للوصول إلى الحل
استراتيجية
التجربة المنظمة
(Systematic Trial)
حل المشكلة بتجربة جميع الاحتمالات بطريقة منظمة لضمان العثور
على الحل الصحيح دون إغفال أي خيار
استراتيجية
تبسيط المشكلة
(Simplifying the Problem)
حل المشكلة بتبسيط الأعداد أو الظروف المعقدة إلى
حالات أصغر
وأسهل، ثم استخدام الحل المبسط للوصول إلى حل المشكلة الأصلية
استراتيجية كتابة قاعدة أو قانون
معروف
(Writing a Rule/Formula)
حل المشكلة بتحديد قاعدة أو
قانون رياضي عام يمثل العلاقة بين
الكميات، بحيث يمكن استخدامه لحل المشكلة الحالية
أو مشكلات مشابهة مستقبلًا.
استراتيجية النمذجة الرياضية
( Mathematical Modeling )
تمثيل (ترجمة) المشكلة رياضيًا باستخدام معادلات متعددة أو رموز لتوضيح
العلاقات بين الكميات،
بهدف فهم المشكلة وحلها رياضياً
نشاط
مصنع ثلج يمكنه انتاج 1000 مكعب طول ضلع
الواحد منها يساوي1 سم .
اذا أراد أن
ينتج مكعبات بطول 2
سم باستخدام نفس الكمية من الماء
فكم مكعب يمكنه أن
ينتج ؟
ما الاستراتيجية؟
كم عدد المكعبات 1 في 1
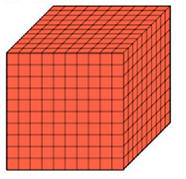
كم عدد المكعبات
2 في 2
نشاط
نجار يمكنه
قص لوح خشبي الى 100مربع صغير طول ضلع
الواحد منها يساوي1
سم
.
اذا أراد أن
ينتج مربعات بطول
2
سم باستخدام
لوح مماثل
فكم
مربعا يمكنه أن
ينتج ؟
ما الاستراتيجية؟
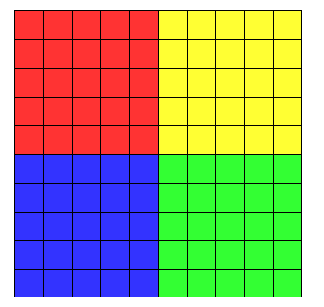
100 مربع بطول 1 سم

25 مربع بطول 2 سم

كم مربعا بطول 5 سم
يمكن عملها بلوح مماثل ؟
4 مربعات بطول 5 سم
نشاط
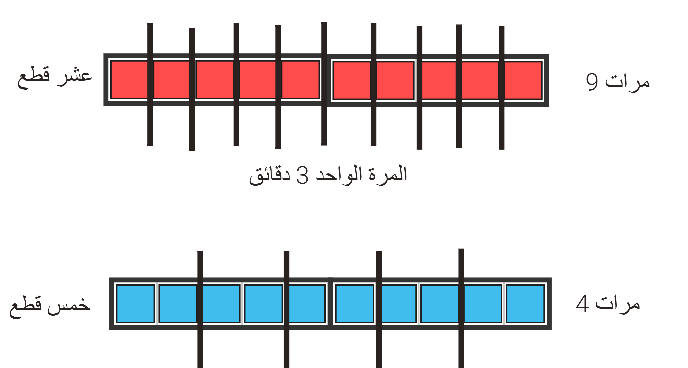
ماسورة من
البلاستيك تم قطعها إلى
خمس قطع متساوية . إذا كان الوقت اللازم لهذه المهمة
12
دقيقة
فما الوقت اللازم لقطع ماسورة مماثلة
الى عشر قطع متساوية ؟
· كل مرة نستخدم فيها آلة القطع نحتاج 3 دقائق.
· للحصول على 10 قطع كم مرة نحتاج ؟
|
عدد مرات الاستخدام |
1 |
2 |
3 |
4 |
5 |
7 |
ن |
|
عدد القطع الناتجة |
2 |
3 |
4 |
5 |
6 |
8 |
؟ |
4 مرات = 12 دقيقة.
المرة الواحدة تحتاج 3 قائق
10 قطع تحتاج 9 مرات قطع = 27 دقيقة.
التمثيل البصري
نشاط
لدى محمد ولدين أعطى كل واحد
منها المبلغ نفسه لشرء دفاتر مدرسية. فاشترى أحدهما 17
دفترا وبقي معه 30 ريالا
واشترى الآخر
19 دفترا وبقي معه 20 ريالا
فكم قيمة الدفتر
الواحد؟
التخمين والتحقق
| الأول 17
دفتر والباقي 30 |
الثاني19 دفتر
والباقي20 |
| القيمة
|
المبلغ |
المجموع |
المبلغ |
المجموع |
| 2 ريال |
34 |
64 |
38 |
58 |
| 4ريال |
68 |
98 |
76 |
96 |
| 5ريال |
85 |
115 |
95 |
115 |
سعر الدفتر الواحد 5 ريال
الأول 17 في 5 +30 =115
الثاني 19 في 5 +20 = 115
كتابة معادلة
نفرض أن المبلغ هو ص
قيمة الدفتر = د
الأول اشترى 17 دفتر
وبقي معه 30 ريال
17 د+30
الثاني اشترى 19 دفتر وبقي
مع 20 ريال
19 د+20
نظرا لتساوي المبلغين يكون
17 د+30 = 19 د+20
د=5
الحل باستخدام
الميزان
https://nrich.maths.org/interactive-environments/interactive-balance
بداية الميزان في حالة توازن

عند اضافة الباقي مع كل منهما في كفة يختل التوازن
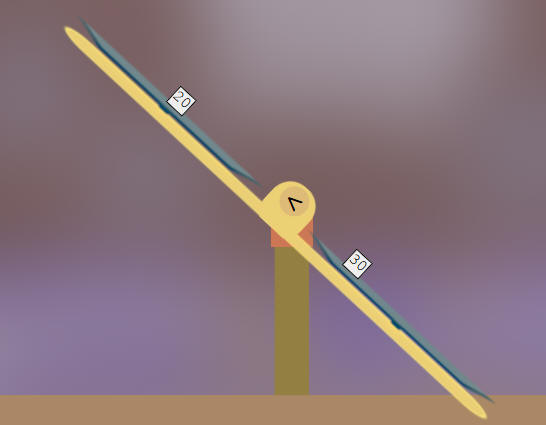
احدهما اشترى 17 دفتر وبقي معه 30 ريال
الآخر اشترى 19 دفتر وبقي معه 20 ريال
على
افتراض أن سعر الدفتر 4 ريال

لا توازن
نجرب سعر الدفتر 5 ريال

يحدث التوازن
وعليه يكون سعر الدفتر هو 5
ريال
نشاط
مسبح
له مضختان الأولى تملؤه في 20 دقيقة والآخرى في 30 دقيقة.
اذا تم استخدام المضختان معا
ففي كم دقيقة يمكن تعبئته؟
الحل
لنفرض أن المسبح يحتوي على
60 طن من الماء
( المضاعف المشترك الأصغر للعددين 20 و 30 )
المضخة الأولى
تملء المسبح في 20 دقيقة أي 3
طن
في الدقيقة الواحدة . ( 60 قسمة 20)
المضخة
الثانية تملء المسبح
في 30 دقيقة أي 2 طن
في الدقيقة الواحدة ( 60 قسمة 30)
المضختان معا تضخان في
المسبح 5 طن في الدقيقة
المضختان تملئان
المسبح (60طن ) في 12 دقيقة
الحل البصري
سعة المسبح 20 في30 = 600 طن
عدد الوحدات 600 كل وحدة تمثل
طن
ما يرد في المسبح في الدقيقة
الواحدة
 |
 |
| واحد على 30 من المسبح
في الدقيقة |
واحد على 20 من المسبح
في الدقيقة |
|
|
|
50على 600 من المسبح
في دقيقة واحدة |
نشاط
ما رقم الصفحة التي
يبدأ فيها الجزء العاشر
من القران الكريم
؟
اذا
كنا نعرف القاعدة فالاستراتيجية هي كتابة معادلة
في حال
عدم معرفتنا بالقاعدة ونريد التعرف عليها
فالاستراتيجية
هي بناء جدول
دراسة الجدول لاكتشاف النمط
والعلاقة في الجدول
استراتيجية بناء جدول
| رقم الجزء |
رقم الصفحة |
| 1 |
2 |
| 2 |
22 |
| 3 |
42 |
| 4 |
62 |
|
5 |
82 |
|
10 |
182 |
| ن |
؟ |
استراتيجية اكتشاف نمط من
الجدول
هل لاحظت أن الفارق هو 20 ؟
حاول أن تجد علاقة بين رقم
الجزء ورقم الصفحة
والفارق الثابت
الجزء
5 مثلا والفارق
20 ورقم الجزء 82
ما العلاقة بين
5 و 20
و 82
هل وجدت علاقة ؟
دراسة العلاقة بين
5
و 20 و 82
الاكتشاف الموجه
| الجزء |
الفرق |
رقم الصفحة |
|
5 |
20 |
82 |
| 10 |
20 |
182 |
5 في 20 =100
كيف نصل من 100 الى 82
5 في 20
ناقص 18
ماذا عن
10 و 20 و 182
10 في 20 =200
كيف نصل من 200 الى 182
10 في 20
ناقص 18
العلاقة هي :
الحد النوني= الفرق ( رقم الحد)
- 18
وبصفة عامة
الحد النوني= الفرق ( رقم الحد) +
( الحد الأول - الفرق )
هل توجد علاقة أخرى ؟
هل لاحظت أن
الفرق 20 و الحد الأول 2
هل لاحظت العلاقة بين
الجزء 5 والحد الأول
2 و مرات تكرارالفرق و الصفحة
82
مرات التكرار= ( رقم
الجزء - 1 )
| رقم الجزء |
رقم الصفحة |
الفرق |
مرات التكرار |
| 1 |
2 |
- |
- |
| 2 |
22 |
20 |
1 |
| 3 |
42 |
20 |
2 |
| 5 |
82 |
20 |
4 |
| 10 |
182 |
20 |
9 |
| ن |
رقم الصفحة |
20 |
( ن - 1 ) |
الحد الأول 2
مرات التكرار= ( رقم
الجزء - 1 )
| الجزء |
الأول |
تكرارالفرق |
الفرق |
رقم الصفحة |
| 5 |
2 |
4 |
20 |
82 |
| 10 |
2 |
9 |
20 |
182 |
رقم الصفحة = الحد الأول + الفرق
( رقم الجزء - 1 )
متتالية
2 22 42 62 82 ---
| الحد |
الأول |
الثاني |
الثالث |
الرابع |
الخامس |
الفرق |
النوني |
| القيمة |
2 |
22 |
42 |
62 |
82 |
20 |
ن |
ن = الحد الأول + الفرق
( ن - 1 )
وهو قانون الحد النوني في المتتاليات الحسابية
ما ملاحظتك حول القاعدتين
الحد النوني =
الفرق ( رقم الحد
) +( الحد الأول
-
الفرق )
الحد النوني = الحد الأول +
الفرق ( رقم الحد
- 1 )
وفقاً
لقانون المتتاليات
الحد النوني = الحد الأول +
الفرق ( رقم الحد
- 1 )
بفك القوس واعادة الرتيب نحصل على
اسهل صياغة
الحد النوني =
الفرق ( رقم الحد
) +(
الحد الأول
-
الفرق )
جدول يوضح رقم الجزء ورقم الصفحة
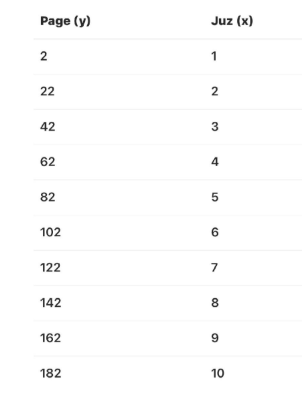
التمثيل على شبكة التربيع
لمعرفة العلاقة
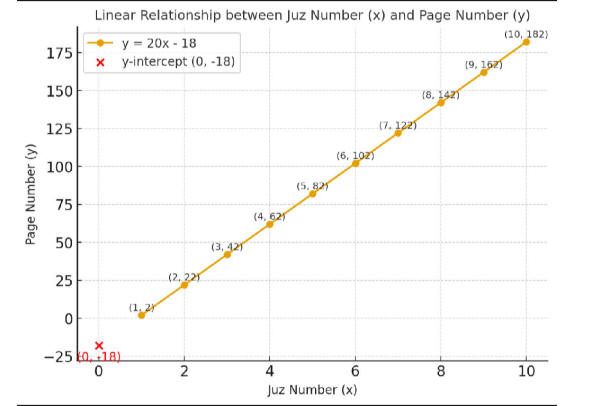
التمثيل على شبكة التربيع
لمعرفة العلاقة
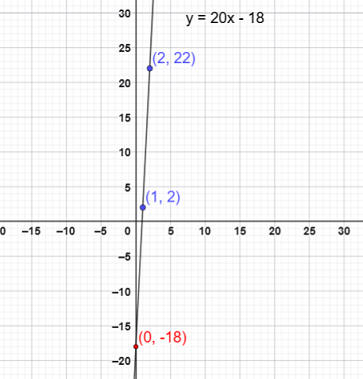
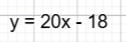
الاستثناءات الرئيسية هي:
الجزء رقم 1
رقم الصفحة 1
من كتب التراث
كيف تعرف رقم الصفحة لكل جزء من القرآن الكريم .
ما رقم الصفحة التي يبدأ فيها الجزء التاسع
| |
|
|
| رقم الجزء |
رقم الجزء
- 1 |
ضعف رقم
الجزء - 1 |
اضافة 2
يمين ضعف رقم الجزء - 1 |
|
9 |
8 |
16 |
162 |
| |
|
|
|
| |
|
|
|
الطريقة
الجزء التاسع أي رقم تسعه
تسعة ناقص واحد = ثمانية
ثمانية ضرب اثنين =
16
ثم نضيف الرقم اثنين إلى يمين الرقم 16 فيصبح 162 وهذا هو رقم الصفحة التي يبدأ بها الجزء التاسع
ما رقم الصفحة التي يبدأ فيها الجزء الحادي
والعشرين
| رقم الجزء |
رقم الجزء
- 1 |
ضعف رقم
الجزء - 1 |
اضافة 2
يمين ضعف رقم الجزء - 1 |
|
21 |
20 |
40 |
402 |
| |
|
|
|
الجزء الحادي
والعشرين
21 ناقص 1
= 20
20 ضرب 2
= 40
نضيف اثنان يمين الرقم 40
يصبح 402
الجزء الحادي
والعشرين يبدأ في الصفحة رقم 402
حاولوا ذلك بأنفسكم
الاستثناء
1. الجزء 1
رقم الصفحة 1
نشاط
قدم أحد مطاعم البيتزا العرض التالي
سعر البيتزا الكبيرة مع
سعر
البيتزا الصغيرة 42ريال
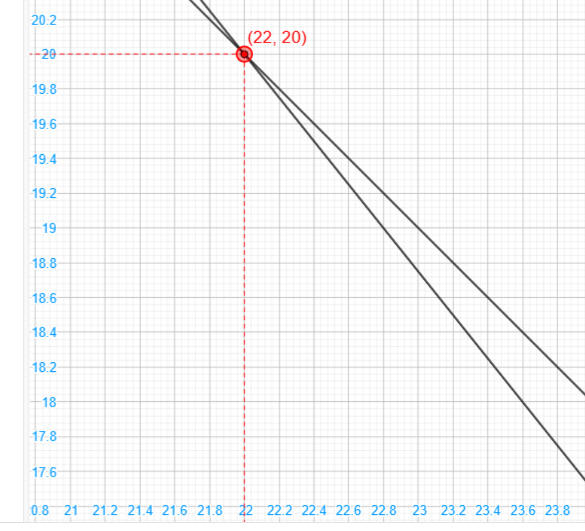
و نصف سعر البيتزا الكبيرة مع خمسي سعر البيتزا الصغيرة 19 ريال
كم سعر البيتزا الكبيرة وكم سعر البيتزا الصغيرة ؟
ما الاستراتيجية المقترحة ؟
استراتيجية النمذجة الرياضية
(كتابة أكثر من معادلة)


التمثيل البصري
| كبيرة |
+ |
صغيرة |
القيمة |
|
 |
|
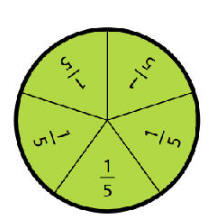
|
42 |
المعادلة 1 |
| |
|
|
|
|
|
نصف الكبيرة |
+ |
خمسي الصغيرة |
19 |
|
|
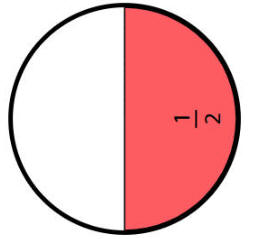
|
+
|
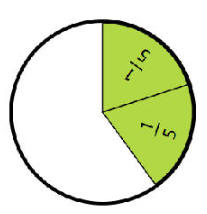
|
19
|
المعادلة 2 |
| |
|
|
|
|
|
نصف الكبيرة |
+ |
خمسي الصغيرة |
19 |
|
 |
|
 |
19
|
المعادلة 2 |
|
بجمع المعادالة 1 مع
المعادلة 2 |
|
 |
|
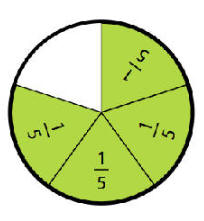 |
38 |
المعادلة 3 |
|
كبيرة +أربعة أخماس الصغيرة = 38 ريال |
|
| |
|
|
|
|
|
بطرح المعادلة 3 من المعادلة 1 |
|
|
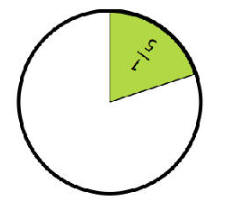
|
4 |
|
|
اذا خمس الصغيرة=
4
فان كامل الصغيرة= 20 |
|
|
|

|
22 ريال |
|
طريقة أخرى
الكبيرة + الصغيرة= 42 ريال
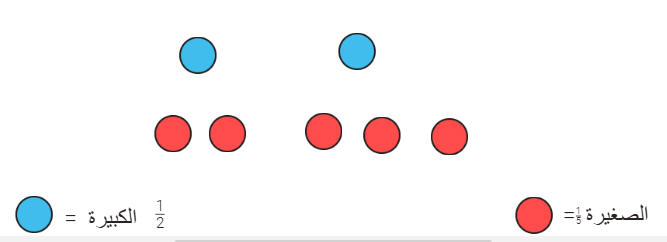
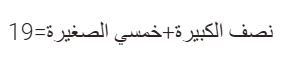
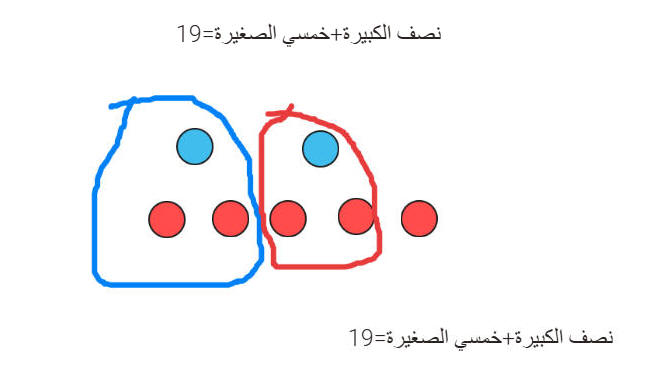
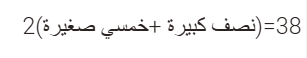
كبيرة + 4 أخماس الصغيرة= 38
ريال
كبيرة +صغيرة= 42 ريال
خمس الصغيرة = 4
الصغيرة=20
حل معادلتين بيانيا
https://aghandoura.com/SITE/EQUAhtml.htm
\
GEOGEBRA
نشاط
في احدى قاعات الأفراح كل
الطاولات من النوع
السداسي المنتظم مرصوصة
الى جوار بعضها
ما العلاقة بين عدد الطاولات
وعدد الراسي؟
هل استراتيجية التخمين
والتحقق مفيدة لحل المشكلة؟
ما القاعدة العامة التي تربط
بين عدد الكراسي وعدد الطاولات؟
الاستراتيجيات الممكنة
استراتيجية
تبسيط المشكلة
استراتيجية
بناء جدول
استراتيجية
التجربة المنظمة
استراتيجية التمثيل البصري
استراتيجية كتابة قاعدة أو قانون
استراتيجية التمثيل البصري
في احدى قاعات الأفراح كل
الطاولات من النوع

مرصوصة الى جوار بعضها
بالطريقة
4 طاولاات
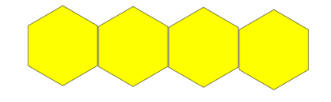
كل الطاولات تحتوي على 4 كراسي +
2 كرسي
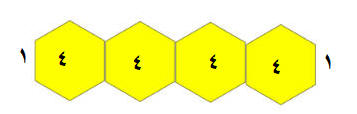
ك= 4ط +2
الطاولات الداخلية فقط
تحتوي على
4كراسي + 2 طاولة من نوع 5 كراسي
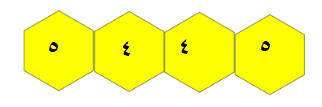
عدد الكراسي يساوي
4( ط -2) +10
يساوي
ك= 4ط +2
استراتيجية
بناء جدول واكتشاف النمط من الجدول
| عدد الطاولات |
عدد الكراسي |
الفرق |
| 1 |
6 |
- |
| 2 |
10 |
4 |
| 3 |
14 |
4 |
| 4 |
18 |
4 |
| ن |
؟ |
؟ |
الفرق بين حالتين متتاليتين 4 كراسي
عدد الكراسي يساوي
4( ط -2) +10
يساوي
ك= 4ط +2
الربط بين الجبر والهندسة
حيث يمكن تمثيل النقاط من الجدول
| عدد الطاولات س |
عدد الكراسي ص |
| 1 |
6 |
| 2 |
10 |
| 3 |
14 |
| 4 |
18 |
| ن |
؟ |
التمثيل على شبكة التربيع
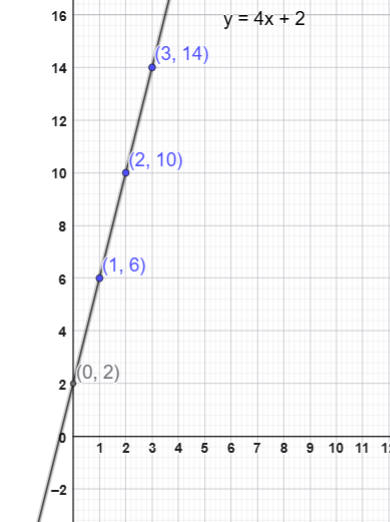
ميل المستقيم =4
الجزء المقطوع من محور
الصادات=2
معادلة المستقيم
ص= 4س +ج
ج= الجزء المقصود من محور
الصادات
بالتعويض عن احاثيات نقطة
نحصل على الجزء المقطوع
اذا اخترنا س=1 و ص =6
ص= أس + ب
6= 4(1)+ ب
ب =2
ص= 4أ +2
نشاط
ما القاعدة في حال كانت
الطاولات ثمانية الشكل
ما العلاقة التي تربط بين عدد
الكراسي وعدد الطاولات ؟
كل الطاولات تحتوي على ستة
كراسي و2 كرسي
موزعةعلى الطاولتين الطرفيتين
الكراسي ك
الطاولات ط

ك= 6ط +2
كل الطاولات الداخلية تحتوي
على ستة كراسي وطاولتين فقط كل طاولة 7 كراسي
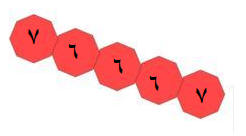
الكراسي ك
الطاولات ط
ك=6(ط
-2) +14
ك= 6ط+2
بالطريقة السابقة يمكن بناء
جدول واستنتاج النمط والقاعدة
والتمثيل على شبكة التربيع
وكتابة معادلة الخط المستقيم
نشاط
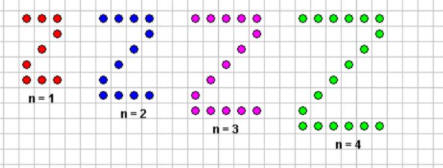
ما السؤال ؟
ما الاسترتيجة المناسبة ؟
السؤال كم عدد النقاط في الشكل رقم خمسين؟
هل تفيد
استراتيجية التخمين والتحقق ؟
ما ذا عن استراتيجية
- بناء جدول
- البحث عن نمط
- كتابة معادلة

|
عدد النقاط |
الشكل |
|
9 |
1 |
|
12 |
2 |
|
15 |
3 |
|
18 |
4 |
|
21 |
5 |
الاستفادة من الفرق
الثابت بين كل حدين متتاليين
|
الفرق |
عدد النقاط |
الشكل |
|
---- |
9 |
1 |
|
3 |
12 |
2 |
|
3 |
15 |
3 |
|
3 |
18 |
4 |
|
3 |
21 |
5 |
هل لاحظت أن :
الحد
الخامس تكرر فيه الفرق 4 مرات
الحد
الرابع تكرر فيه الفرق 3
مرات
الحد
الثالث تكرر فيه الفرق 2
مرة
الحد
ن
تكرر فيه الفرق (ن-1) مرة
هل ممكن استنتاج
قاعدة ؟
الحد
الخامس = الحد الأول
+ 4ضرب الفرق
الحد الرابع = الحد الأول +3
ضرب الفرق
الاستراتيجية المناسبة
استراتيجية
كتابة قاعدة أو قانون
(Writing a Rule/Formula)
حل المشكلة بتحديد قاعدة أو قانون رياضي عام
يمثل العلاقة بين
الكميات، بحيث يمكن استخدامه
لحل المشكلة الحالية أو مشكلات مشابهة مستقبلًا.
قانون
الحد العام لمتتالية حسابية
الحد النوني
an=a1+(n-1)d
d=
الفرق
بين حدين متتاليين
a1 =
الحد الأول
n=
رقم الحد
من
الجدول نلاحظ ان الشكل الخامس فيه 21 نقطة
|
الفرق |
عدد
النقاط |
الشكل
رقم |
|
3 |
21 |
5 |
نطبق القانون
an=a1+(n-1)d
الحد الأول
=9
الفرق=3
الحد
الخامس = 9 +4(3)=21
قانون بديل وسريع
(
اعادة كتابة القانون )
an=a1+(n-1)d
an=a1+nd- d
an=nd
+ a1- d
الحد
المطلوب = (
الفرق
x رقم الحد
) +
( الحد الأول
- الفرق )
3ن + 6
الحد الخامس = 3(5) +6 =21
|
الفرق |
عدد
النقاط |
الشكل
رقم |
|
3 |
21 |
5 |
ماذا لو كان
السؤال كم
مجموع
عدد النقاط في
كل الخمسين شكل الأولى ؟

ما الاستراتيجية المناسبة ؟
جدول المجموع
|
المجموع |
عدد النقاط |
الشكل |
|
9 |
9 |
1 |
|
21 |
12 |
2 |
|
36 |
15 |
3 |
|
54 |
18 |
4 |
|
75 |
21 |
5 |
كيف حصلنا على مجموع الخمس حدود
الأولى ؟
عدد الحدود 5
الأول 9 نقاط
الخامس
21 نقطة
المجموع = عدد الحدود (الأول +الخامس ) قسمة 2
= 5(9+21) قسمة 2= 75
قانون مجموع حدود متتالية حسابية
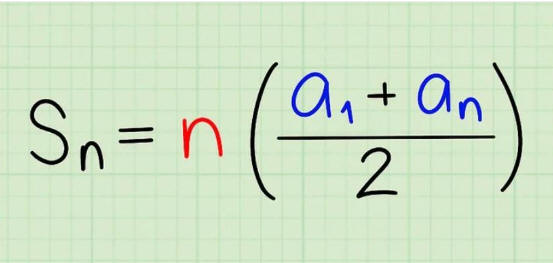

مسئل محلولة مشابهة على الرابط
https://aghandoura.com/METEEBNEWNEW/LEVELS.htm
نشاط
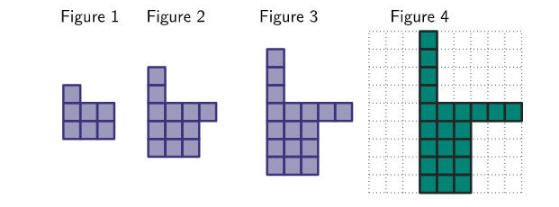
احسب عدد المربعات في الحد العاشر
لمعرفة قاعدة النظام قم ببناء جدول من خانتين
واكتب عدد المربعات في كل حد كما يلي
|
الحد |
عدد المربعات |
|
الأول |
7 |
|
الثاني |
12 |
|
الثالث |
17 |
|
الرابع |
22 |
|
الخامس |
27 |
|
السادس |
32 |
|
ن |
? |
الفرق الثابت d=5
الحد النوني = 5ن+2
الحد الأول = الفرق +؟
7=5+2
الحد النوني = 5 ن +2
التأكد
الحد الخامس = 27 ن=5 رتبة الحد
الحد الخامس= 5 في 5 +2
البرمجية على الرابط
https://aghandoura.com/SIGMA/PAT.html
ما
الاستراتيجية المناسبة
الاستراتيجية المناسبة
استراتيجية
كتابة قاعدة أو قانون
(Writing a Rule/Formula)
حل المشكلة بتحديد قاعدة أو قانون رياضي عام
يمثل العلاقة بين
الكميات، بحيث يمكن استخدامه
لحل المشكلة الحالية أو مشكلات مشابهة مستقبلًا.
قانون
مجموع متتالية حسابية
نشاط
الحاسبة
بدأ محمد بالتوفير فقرر أن يضع
في اليوم الأول 100
ريال
في الحصالة .
وفي كل يوم
يضع خمس ريالات
زيادة عن اليوم السابق .
فكم ريالا
يجب عليه أن يضع
في يومه الخامس.؟
الحد ن =
الأول
+
الفرق ( ن -1)
أو
الحد
المطلوب = (
الفرق x رقم الحد ) + ( الحد الأول
- الفرق )
|
اليوم |
المبلغ
|
الفرق |
|
1 |
100 |
5
|
|
2 |
105 |
|
3 |
110 |
5 |
|
4 |
115 |
|
5 |
120 |
5 |
|
6 |
125 |
|
ن |
|
|
العلاقة 5ن +
95
يمكن
حساب العلاقة
من الفرق ومبلغ اليوم الأول.
مبلغ
اليوم الأول
= 10
الفرق =5
العلاقة
ايداع يوم محدد يمكن حسابه بالعلاقة
الحد المطلوب
= (
الفرق
x
رقم الحد ) + ( الحد الأول
- الفرق )
حاسبة المجموع
نشاط ما المبلغ الموجود
في الحصالة بعد 10 يوم؟
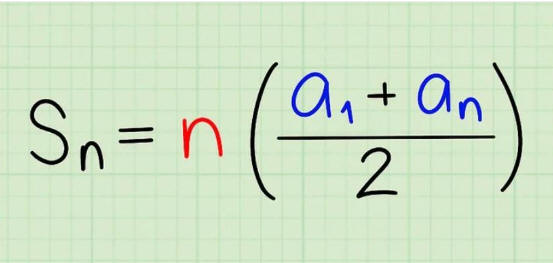
الحد الأول 100
الحد العاشر 145
الفرق 5
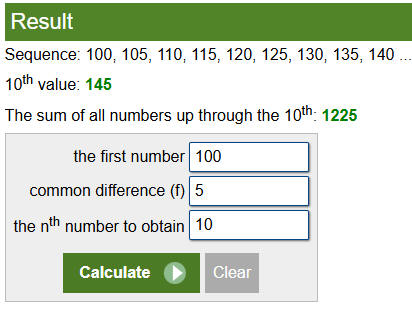
ما
الحد العاشرفي التسلسل؟
1,3,5,7,9,11
الحد
الأول =1
الفرق= 2
الجدول
لمن لايعرف القاعدة
|
الحد |
القيمة |
الفرق |
القاعدة |
|
1 |
1 |
2
|
2ن - 1 |
|
2 |
3 |
|
3 |
5 |
2 |
|
4 |
7 |
|
5 |
9 |
2 |
|
6 |
11 |
|
ن |
|
|
| |
|
|
العاشر يعني ن= 10
الحد الأول =1
الأساس (الفرق)
= 2
الحد ن =
الأول
+
الفرق ( ن -1)
الحد
العاشر
= الأول + 2(10-
1)
الحد
العاشر
= 1 +
2(9)
الحد
العاشر
= 19
قيمة الحد ممكن معرفته بالعلاقة :
الحد المطلوب
= (
الفرق
x
رقم الحد ) +
( الحد الأول
- الفرق )
نشاط
نشاط ماذا لوكان المطلوب حساب
مجموع ألخمسين حد الأولى من المتسلسة نفسها
1,3,5,7,9,11
بعد بناء جدول المجموع يمكن
استنتاج قاعدة مجموع الأعداد الفردية
محموع الأعداد الفردية = مربع
عددها
فالمتتالية السابقة عدد حدودها
خمسة حدود ومجموع حدوها الستة =ستة تربيع=36
نصف (الأول
+الأخير )( عدد الحدود )
استراتيجية
كتابة قاعدة أو قانون
(Writing a Rule/Formula)
نشاط
عددان مجموعهما 25، وحاصل ضربهما 144. أوجد العددين.
استراتيجية
كتابة قاعدة أو قانون
العددان س و (25- س)
س (25- س) = 144
25س - س2=144
س2 - 25س +144= 0
(س-9)(س-16)=0
س=9
س=16
ممكن حله
باستراتيجية التخمين والتحقق
استراتيجية التخمين والتحقق
(Guess and Check)
حل المشكلة بالتخمين لقيمة المجهول
ثم التحقق مما إذا كانت تحقق شروط المشكلة،
وتكرار العملية
حتى الوصول للحل الصحيح
نخمن حلاً، ثم نتحقق إن كان يحقق الشروط، ونعدّل
التخمين حتى نصل للحل الصحيح.

| تخمين |
عجلتين |
عجلات |
3 عجلاات |
عجلات |
مجموع |
مقارنة |
| 1 |
3 |
6 |
3 |
9 |
15 |
اكبر |
| 2 |
4 |
8 |
2 |
6 |
14 |
صحيح |
| 3 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
التمثيل البصري
نعتبر كل الدراجات الستة من النوع ذي العجلتين
الباقي عجلتين للنوع الثاني من الدراجات
2 دراجة من نوع 3 عجلاات
نشاط
في حفلة مدرسية، كان عدد الحضور ٨٠ شخصًا.
سعر تذكرة الطالب ١٠ ريالات، وسعر تذكرة المعلم ٢٥ ريالًا.
إذا كان إجمالي الدخل من التذاكر ١٢٢٠ ريالًا،
فكم عدد الطلاب وكم عدد المعلمين؟
نخمن قيم
لعدد الطلاب ونختبر (الدخل من الطلاب + الدخل من المعلمين
)
شرطين
العدد الكلي 80 شخص و الدخل
الاجمالي 1220ريال
| ت |
عدد
الطلاب |
دخل
الطلاب |
عدد
المعلمين |
دخل
المعلمين |
الدخل |
1220 |
| 1 |
70 |
700 |
10 |
250 |
950 |
أقل |
| 2 |
60 |
600 |
20 |
500 |
1100 |
أقل |
| 3 |
50 |
500 |
30 |
750 |
1250 |
أكبر |
| 4 |
52 |
520 |
28 |
700 |
1220 |
يساوي |
في
أربع خطوات وصلنا للحل
الدخل
الحقيقي 1220ريال
ماذا لو
فرضنا أن عدد الطلاب = 40 وعدد المعلمين = 40
| ت |
عدد
الطلاب |
دخل
الطلاب |
عدد
المعلمين |
دخل
المعلمين |
الدخل |
1220 |
| 1 |
40 |
400 |
40 |
1000 |
1400 |
أكبر |
الفرق
بين هذا الدخل والدخل الحقيقي 180 ريال
الفرق
بين تذكرة المعلم وتذكرة الطالب 15 ريال
استبدال
معلم واحد بطالب واحد يقلل الدخل 15 ريال
نحتاج
تقليل 180 ريال باستبدال 12 معلم
180 قسمة
15 = 12
فيكون
عدد المعلمين 40 ناقص 12= 28 معلم
عدد
الطلاب 52 طالب
كيف ممكن
تقليل عدد التخمينات؟
ممكن تقليل عدد
التخمينات
باختيار 40 معلم
و 40 طالب
هل ممكن
الحل في خطوة واحدة ؟
الحل في
خطوة واحدة:
الدخل
الحقيقي 1220 ريال
اذافرضنا
أن كل الحضور طلاب . الدخل الافتراضي 800 ريال
الفرق بين
الدخل الحقيقي والدخل الافتراضي 1220 ناقص 800 = 420 ريال
الفرق بين
قيمة تذكرة المعلم وتذكرة الطالب = 25
- 10 =15 ريال
عدد
المعلمين = الفرق بين الدخلين قسمة الفرق بين سعر تذكرة
المعلم وسعر تذكرة الطالب
عدد
المعلمين = 420 قسمة 15= 28 معلم
عدد
الطلاب = 80 -
28= 52 طالب.
استراتيجية النمذجة
الرياضية
( Mathematical
Modeling )
تمثيل المشكلة رياضيًا
باستخدام
معادلات متعددة
أو رموز لتوضيح العلاقات بين الكميات،
بهدف فهم
المشكلة وحلها رياضياً
في حفلة مدرسية، كان عدد الحضور ٨٠ شخصًا.
سعر تذكرة الطالب ١٠ ريالات، وسعر تذكرة المعلم ٢٥ ريالًا.
إذا كان إجمالي الدخل من التذاكر ١٢٢٠ ريالًا،
فكم عدد الطلاب وكم عدد المعلمين؟
T+S=80
25T+10S=1220
نشاط
عددان مجموعهما
100، والفرق بينهما
50
ما العددان؟
استراتيجية النمذجة
الرياضية
( Mathematical
Modeling )
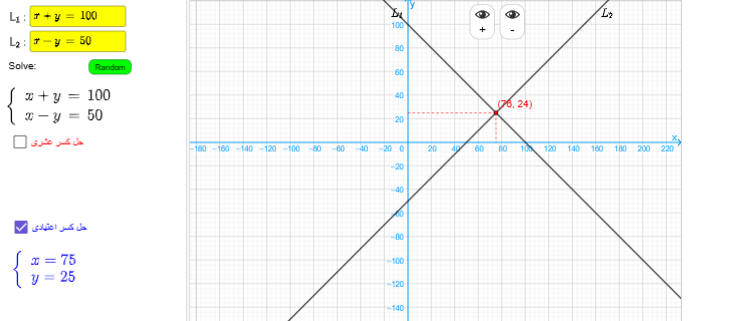
x+y=100
x-y=50
استراتيجية التخمين والتحقق
(Guess and Check)
• نخمن
60 و
40
الفرق 20
• نخمن
70 و
30
الفرق 40
نخمن
80 و 20
الفرق 60
نخمن 75 و 25
الفرق 50
العددان
75 و
25
لتقليل عدد المحاولات
نعتبر أن العددين 50 و 50
الحاسبة
نشاط
ماالعددان اللذان مجموعهما 117 والفرق بينهما 17 ؟
ما
الاستراتيجية المناسبة
استراتيجية النمذجة
الرياضية
( Mathematical
Modeling )
تمثيل المشكلة رياضيًا
باستخدام معادلات متعددة
أو رموز لتوضيح العلاقات بين الكميات،
بهدف فهم
المشكلة وحلها رياضياً
x+y=117
x-y=17
مزيد من التمارين
المحلولة
https://www.aghandoura.com/The%20ratio/main.htm
طريقة ابداعية بدون معادلاات
ماالعددان اللذان مجموعهما 117 والفرق بينهما 17 ؟
تتلخص الطريقة في الخطوات التالية :
-
حساب الفرق
بين مجموع العددين والفرق بينهما
- قسمة الفرق
بين مجموع العددين والفرق بينهم على 2 ينتج العدد الأصغر
المثال :
117
ناقص 17
يساوي 100
العدد
الأصغر= نصف الفرق
أي 100 قسمة 2
الأصغر= 50
العدد الأكبر =
المجموع - الأصغر
الأكبر= 117- 50
67=
الأكبر
==================================================================
أرض مستطيلة
الشكل محيطها 500 وعرضها
يساوي ربع طولها
احسب
مساحة الأرض
ما
الاستراتيجية المناسبة للحل ؟
استراتيجية النمذجة
الرياضية
( Mathematical
Modeling )
الطول + العرض= 250
الطول = 4(العرض )
استراتيجية التمثيل البصري
المحيط = 500
نصف المحيط ( الطول+العرض)
الطول = 4( العرض )
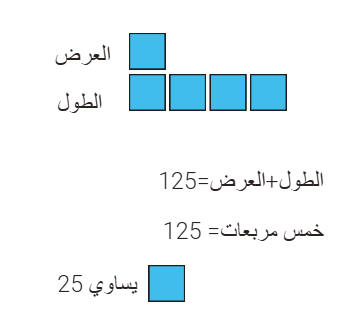
الطول =100
العرض=25
استراتيجية بناء جدول
(Table Strategy)
تنظيم البيانات والمعلومات في جدول مرتب لتوضيح العلاقات
بين الكميات
ورؤية الحل بطريقة منظمة.
تنظيم المعطيات في جدول يساعد على رؤية الحل
بسهولة.
نشاط
صف
خامس ابتدائي

لدى محمد
258
ريال . سعر كيلو
العنب 18 ريال . سعر
كيلو الموز 22 ريال .
اشترى محمد
عدد من كيلوات من
العنب وعدد
من كيلوات من
الموز.
ما
الخيارات الممكنة من
الكيلوات من كل نوع
إذا كان عدد الكيلوات
عدد صحيح ؟
الجدول
| الحالة |
ع=18 |
المبلغ |
م=22 |
المبلغ |
المجموع |
الفرق |
الفرق |
| 1 |
5 |
90 |
5 |
110 |
200 |
58 |
|
| 2 |
6 |
108 |
6 |
132 |
240 |
18* |
قيمة كيلو عنب |
| 3 |
7 |
126 |
6 |
132 |
258 |
|
|
7 كيلو عنب
بمبلغ
126
6 كيلو موز بمبلغ
132
طريقة أخرى؟
لدى محمد
258 ريال
. سعر كيلو العنب 18 ريال . سعر كيلو الموز 22 ريال
كم كيلو من كل نوع يمكنه أن
يشتري ؟
أعداد صحيحة من الكيلوات
اذا اعتبرنا أن محمد اشترى عنب فقط فكم كيلو
يمكنه أن يشتري ب 258 ريال ؟
258 قسمة 18 = 14,333333
14 كيلو بسعر اجمالي قدره 14(18)=252
258-252=6 ريال
اذا استبدلنا واحد كيلو عنب
بكيلو موز راح يزيد المبلغ 4 ريال ( الفرق بين سعر كيلو موز وكيلو عنب )
نبدأ بتخمين 7 كيلو عنب و 7 كيلو
موز
المبلغ 258
| الحالة |
عنب18 |
مبلغ |
موز22 |
مبلغ |
مجموع |
مقارنة |
| 1 |
7 |
126 |
7 |
154 |
280 |
أكثر |
| 2 |
7 |
126 |
6 |
132 |
258 |
نفس المبلغ |
نشاط
عددان مجموعهما 25، وحاصل ضربهما 144. أوجد العددين.
المجموع 25، وحاصل ضربهما 144
|
الحالة |
الأصغر |
الأكبر |
المجموع
|
حاصل
الضرب |
المساواة |
|
1 |
12 |
13 |
25 |
156 |
لا |
|
2 |
11 |
14 |
25 |
154 |
لا |
|
3 |
10 |
15 |
25 |
150 |
لا |
| 4 |
9 |
16 |
25 |
144 |
نعم |
ملاحظ يمكن ترشيد عدد
المحاولات باختيارعددين يكون آحاد
حاصل ضربهما 4
يمكن الحل بكتابة معادلة
الأول س
الثاني (25
-
س)
س (25-
س) = 144
25 س - س تربيع = 144
س تربيع - 25س +144= صفر
(س-9)(س-16) = 0
الأول = 9
الثاني=16
التحقق
مجموعهما 25
حاصل ضربهما =144
نشاط
عددان
مجموعهما 340 وثلثا أحدهما
يساوي ثلاثة أرباع الآخر .
فما هما العددان ؟
يمكن حل
السؤال بأكثر من استراتيجية مثل :
التخمين
والتحقق
بناء
جدول
النمذجة الرياضية
التمثيل البصري
التخمين والتحقق
عددان
مجموعهما 340 وثلثا أحدهما
يساوي ثلاثة أرباع الآخر .
فما هما العددان ؟
من المعطيات ثلثا أحدهما يساوي
ثلاثة أرباع الآخر. وحيث ان الثلثين قريبة من
الثلاثة أرباع
يمكن التخمين أن العددين متساويان
أحدهما 170 والآخر 170 ونظرا لأن 170 لا تقبل القسمة على
ثلاثة نختار 180 ونختبر ذلك التخمين .
الأول 180 الآخر 160
ثلثا الأول 120 و ثلاثة أرباع الآخر 120 . وهما متساويان .
وعليه الأول 180 والآخر 160
بناء
جدول
قبل بناء الجدول يجب دراسة المعطيات . أحد المعطيات
ثلثا الأول تعني أن الأول
يجب
أن يقبل القسمة على ثلاثة .
|
الحالة |
الأول |
الثاني |
ثلثا الأول
|
ثلاثة أرباع الثاني
|
المساواة |
|
1 |
150 |
190 |
100 |
142,5 |
لا |
|
2 |
180 |
160 |
120 |
120 |
نعم |
|
3 |
|
|
|
|
|
استراتيجية النمذجة الرياضية
( Mathematical Modeling )
تمثيل المشكلة رياضيًا
باستخدام معادلات متعددة أو
رموز لتوضيح العلاقات بين الكميات،
بهدف فهم المشكلة وحلها
رياضياً
نشاط
عددان
مجموعهما 340 وثلثا أحدهما يساوي
ثلاثة أرباع الآخر .
فما
هما العددان ؟
استراتيجية النمذجة
الرياضية
النسبة
بين العددين
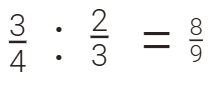
x+y=
340
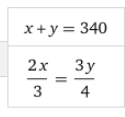
8x=9y
نكمل
الحل بالتعويض

استراتيجية التمثيل البصري
(Visual Representation )
تمثيل المشكلة باستخدام رسوم، أشكال ، أو أي تمثيل بصري
لتوضيح العلاقات بين الكميات
مما يسهل فهم المشكلة والوصول
للحل .
نشاط
عددان
مجموعهما 340 وثلثا أحدهما يساوي
ثلاثة أرباع الآخر .
فما
هما العددان ؟
النسبة
بين العددين
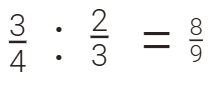
أحدهما 8
مربعات والآخر 9 مربعات
ثلاثة
أرباع الثمانية = ثلثي التسعة
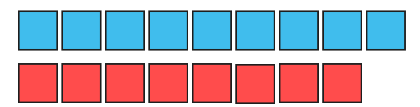
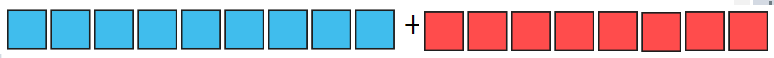
17 مربع=
340
المربع
الواحد= 20
أحدهما
180
الآخر
160
نشاط
لدى محمد
ضعف
ما لدى صالح من المال . و بعد أن انفق صالح ٤٨
ريال وأنفق محمد ١٢٠ ريال
أصبح لدى كل منهما المبلغ نفسه .
فكم
ريالاً بقي مع كل منهما ؟
محمد ضعف صالح

محمد صرف 48 ريال
صالح صرف 120 ريال
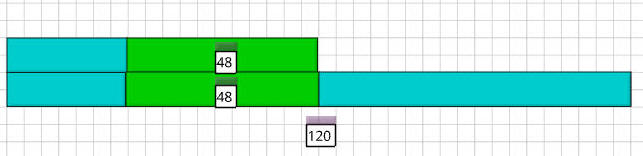
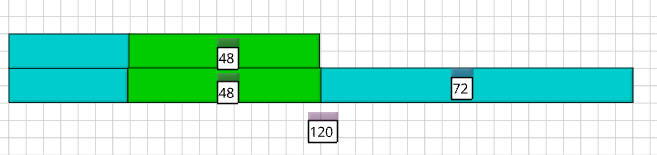
الباقي مع كل منهما 24 ريال
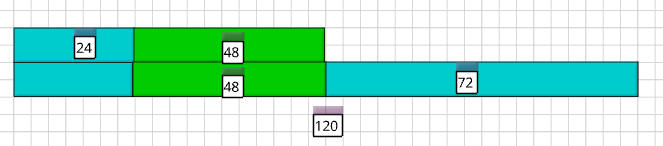
كان مع صالح 72 ريال
كان مع محمد 144 ريال
التأكد
صالح = 72 - 48= 24
محمد= 144- 120=24
نشاط
عددان مجموعهما 100 والفرق بينهما 50
ما العددان ؟
نبدأ من المنتصف ونفرض أن
العددين 50 و 50 الفرق صفر
المطلوب ان يكون الفرق بينهما 50
نصف هذا الفرق = 25
نضيف 25 الى احدهما ونطرح 25 من الآخر
الأكبر= 75
الأصغر=25
الحل باستخدام
الميزان
https://nrich.maths.org/interactive-environments/interactive-balance

نشاط
عددان مجموعهما 25 وحاصل ضربهما
144 فما العددان ؟

نشاط
عددان مجموعهما 15 والفرق بينهما 3 ؟
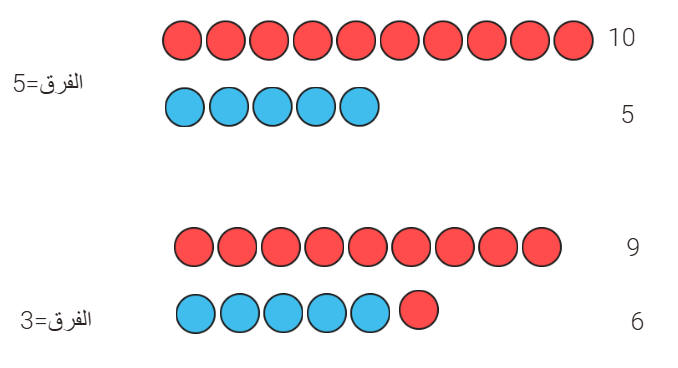
استراتيجية
البحث عن نمط
(Look for a Pattern)
حل المشكلة عن طريق ملاحظة نمط أو تسلسل بين
القيم لتحديد الحل أو التنبؤ بالقيم
المستقبلية
الهدف :
اكتشاف نمط تسلسلي في
أعداد أو
أشكال
للوصول إلى القاعدة العامة.
مثال على التسلسل في
الأعداد
اكتشف قاعدة التسلسل
3 6
9 12 15 18 21 .....
نكتب النمط التسلسلي في
الأعداد
في جدول
للوصول إلى القاعدة العامة.
الجدول
|
الحد |
القيمة |
الفرق |
القاعدة |
|
1 |
3 |
3
|
3ن
|
|
2 |
6 |
|
3 |
9 |
3 |
|
4 |
12 |
|
5 |
15 |
3 |
|
6 |
18 |
|
ن |
|
|
| |
|
|
الحد المطلوب
= (
الفرق x
رقم الحد ) + ( الحد الأول
- الفرق )
مثال على التسلسل في
الأشكال

بالنظر الى الشكل نجد أنه
يسير وفق نمط معين
والهدف هو اكتشاف هذا النمط
النمط
1 ,3 ,6, 10 ,15 , .....

الاستعانة بجدول
|
الشكل |
المكعبات |
|
الأول |
1 |
|
الثاني
|
3 |
|
الثالث |
6 |
|
الرابع
|
10 |
|
الخامس |
15 |
|
السادس |
21 |
| |
|
الثالث (3) و
الرابع (4) والخامس (5)
كيف نصل الى
10 ( الحد
الرابع ) من 4 و 5 ؟
طبق ما توصلت اليه
على
الرابع 10 و
الخامس 15
كيف نصل الى 15 من
5 و6 ؟
1 3 6 10 15 21 .....
نحاول ايجاد طريقة نعرف بها معرفة قيمة حد معين من
خلال رقم الحد
والحد الذي يليه
بعد اختبار المحاولات نجد أن العشرة =( 4 في 5 )
قسمة 2
قيمة الحد = (
رتبة الحد ضرب
الحد الذي يليه ) قسمة 2
من الجدول السابق نلاحظ أن
الخامس=خمسة في 6 = 30
قسمة 2= 15
نشاط
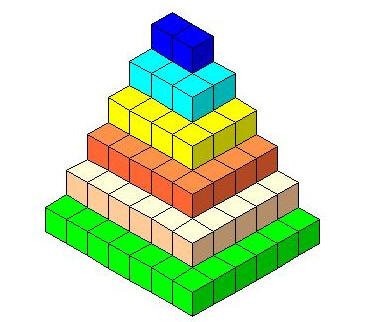
استراتيجية
البدء من النهاية.
(Working Backwards)
حل المشكلة بالبدء من النتيجة النهائية، ثم
الرجوع خطوة خطوة للخلف للوصول إلى الحل
نشاط
يوفر سلطان يوميا مبلغ من
المال يساوي ضعف المبلغ الذي يوفره في اليوم السابق
اذا كان قد وفر 48 ريالا في
اليوم الرابع .فكم ريال وفر في يومه الأول ؟
نبدأ من اليوم الرابع الى
الثالث الى الثاني الى الأول
|
اليوم |
المبلغ
|
|
الأول |
6 |
|
الثاني |
12 |
|
الثالث |
24 |
|
الرابع |
48 |
| |
|
| |
|
نشاط
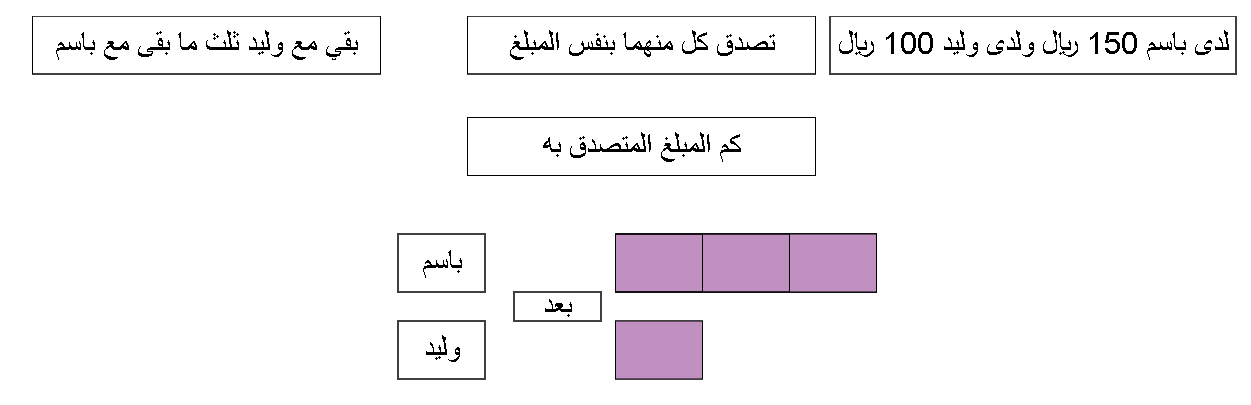
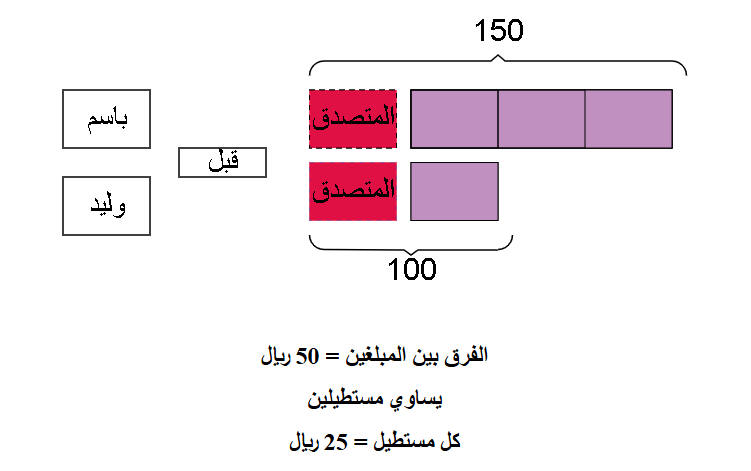
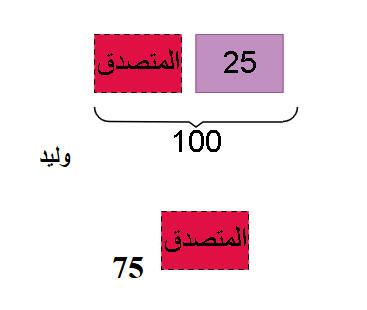
لدى باسم 1176 ريال ولدى
وليد750 ريال . تصدق كل منهما بنفس المبلغ .
بقي مع وليد
ثلث ما بقي مع باسم .
فكم المبلغ المتصدق به؟
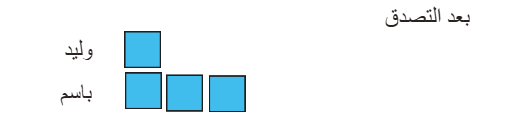
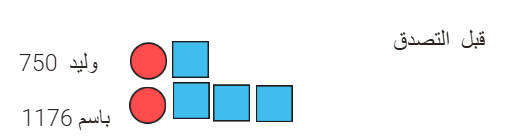

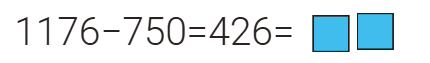
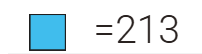

 =537
=537
الفكرة:
نبدأ من النتيجة النهائية ونعمل عكسيًا حتى نصل
إلى البداية.
نشاط
نشاط
لدى
محمد مبلغ
من المال صرف نصفه ثم
صرف ثلث
الباقي
فأصبح
لديه 20ريالا
فكم كان معه بداية
؟
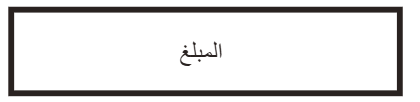
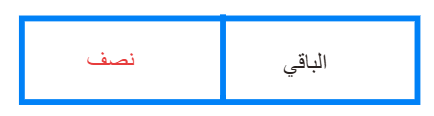
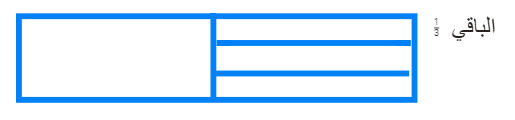
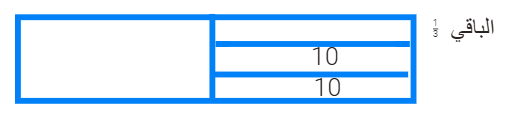
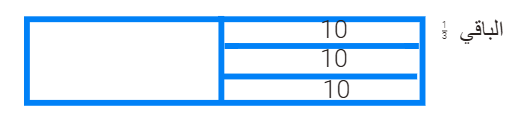
المبلغ= 60 ريال
استراتيجية
البدء من النهاية.
(Working
Backwards)
نبدأ بالعكس
: آخر مرة
صرف ثلث المبلغ الأخير
وبقي 20 ريال هذا الباقي
(20) يمثل ثلثي
المبلغ السابق
وعليه الثلث = 10
يعني أن كامل المبلغ =
30
وعليه يكون المبلغ السابق
30 ريال وهذا يمثل نصف
ما كان عنده بداية
.
المبلغ
في البداية كان 60 ريال .
التأكد
:
كان عنده
60ريال صرف نصفها اصبح معه
30 ريال .
كان عنده
30ريال صرف ثلها أي
صرف 10
اذا الباقي
ثلثين وهو يعادل ما بقي معه
20
وبالتالي الحل صحيح
استراتيجية التمثيل البصري
(Visual Representation )
نشاط


التمثيل البصري
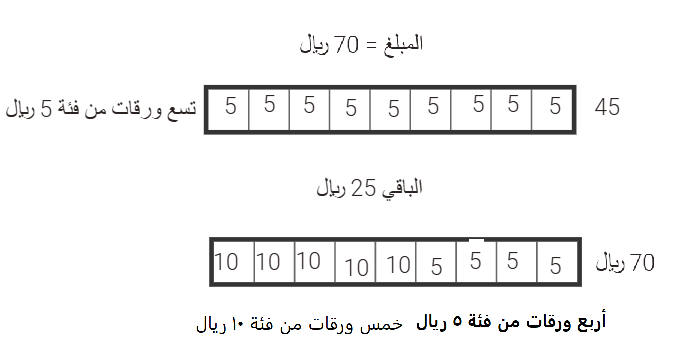
تمثيل مشابه

4 ورقات من فئة الخمس ريال
بمجموع 45 ريال
5 ورقات من فئة العشرريال
بمجموع 50 ريال
يصرف
محمد خمسي راتبه على المسكن و نصف
الباقي من الراتب يصرفه
على المعيشة
ويبقى معه 900 ريال .فكم راتبه.؟
الراتب

خمسي الراتب على السكن
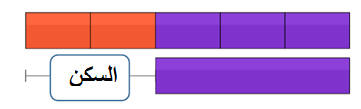

الباقي
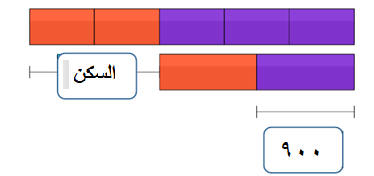
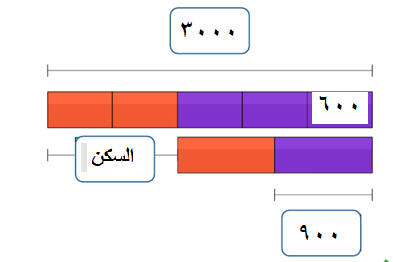
الفكرة:
رسم شكل أو مخطط يساعد على فهم المعطيات والعلاقات.
نشاط
نصف
ما محمد يساوي
ثلاثة أرباع ما مع صالح . فاذا كان
مجموع ما
معهما 150 ريال .
فكم كان مع كل منهما ؟
نحسب النسبة بينهما نصف الى 3 أرباع
نصف على
ثلاثة أرباع = أربعة على ستة
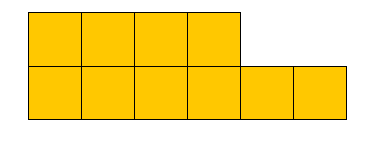
محمد 4 مربعات و صالح 6 مربعات
محمد+ صالح= عشر
مربعات =150
ريال
كل مربع =15 ريال
محمد
40 ريال
صالح
90 ريال
نشاط
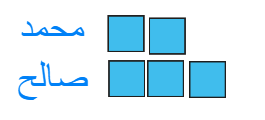
لدى محمد ثلثي ما لدى صالح فاذ
كان مجموع ما معهما معا 160 ريال.
فكم كان مع كل
منهما ؟
محمد 2 مربع
صالح 3 مربعات

نشاط
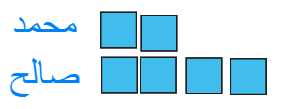
لدى
محمد
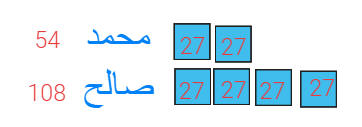
نصف ما مع صالح .اذا أعطى صالح 27 ريال لمحمد
يصبح مع كل منهما
المبلغ
نفسه .
فكم مع كل منهما ؟
بداية ما مع محمد = نصف ما مع
صالح
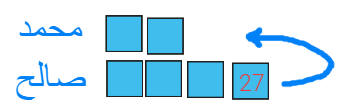
بعد اعطاء صالح 27 ريال لمحمد صار مع كل منهما
المبلغ نفسه
نشاط
لدى
محمد أربعة أضاعف ما مع صالح .اذا أعطى صالح
210 ريال لمحمد
يصبح
مع كل منهما المبلغ
نفسه .
فكم مع كل منهما ؟
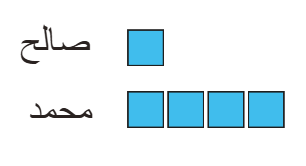
محمد يعطي صالح مربع ونصف مربع
وهو يعادل 210
وعليه تكون قيمة المربع الواحد 70
ريال
صالح = 70 ريال
ومحمد 280 ريال
استراتيجية النمذجة
الرياضية
( Mathematical
Modeling )
تمثيل المشكلة
رياضيًا باستخدام
معادلات متعددة
أو رموز لتوضيح العلاقات بين
الكميات،
بهدف فهم المشكلة وحلها رياضياً
الفكرة:
نحوّل المسألة إلى معادلة رياضية ونحلها.
نشاط
شركة نقل لديها حافلات من نوعين.
النوع الأول حمولة 40
راكب.
والنوع الثاني حمولة 45 راكب .
اذا نقلت الشركة 505
أشخاص في
12 حافلة من
النوعين .
فكم حافلة من كل نوع؟
يمكن الحل:
- التخمين
والتحقق
- بناء جدول
الحل
بنظم المعادلات ( معادلتين في مجهولين )
نفرض أن
:
عدد
حافلات من النوع الأول
x
عدد حافلات
من
النوع الثاني
y
x+y=12
40x+45y=505
نكمل الحل
أو بمجهول واحد
النوع الأول
x
النوع الثاني
12 ناقص
X
نكمل الحل
حل
ابداعي بدون معادلات
لطالب ابتدائي
نجرب
الحافلات الأقل حمولة
12 حافلة
بالحمولة الأقل = 480 شخص
المطلوب 505
الفرق
505-480= 25
الفرق بين
حمولة الحافلتين = 45
-40= خمسة
ركاب
الفرق بين
الحمولةالمطلوبة والحمولة الأقل هو 20
شخص
عدد الحافلات
الكبيرة = ( فرق بين حمولة الركاب)
قسمة
(الفرق بين حمولة الباصين )
عدد الحافلات
الكبيرة= 5
عدد
الحافلات الصغيرة = 7
التأكد 5 في
45 =225
7 في 40= 280
عدد االحافلات
12
الحمولة 505
استراتيجية النمذجة الرياضية
( Mathematical Modeling )
تمثيل المشكلة رياضيًا
باستخدام معادلات متعددة أو
رموز لتوضيح العلاقات بين الكميات،
بهدف فهم المشكلة وحلها
رياضياً
x+y=12
40x+45y= 505
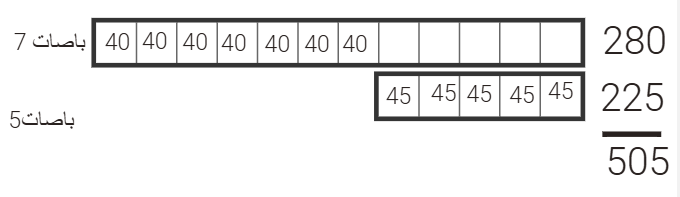
استراتيجية التمثيل البصري
(Visual Representation )
بجعل
كل الباصات من النوع 40 راكب

العدد الكلي 505 راكب
الباقي= 505 - 480= 25 راكب
استبدال باص واحد حملة 45 راكب يزيد عدد
الركاب خمسة
نحتاج خمس باصات من النوع 45 راكب
====================================================================
نشاط
مجموع ما
مع محمد وصالح 500 ريال . فاذا كان
ثلثا ما مع
صالح
و
ثلاثة أرباع ما مع
محمد 340 ريال . فكم
ريال مع كل منهما ؟
استراتيجية النمذجة الرياضية
( Mathematical Modeling )
المعادلة
الأولى
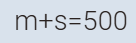 #1
#1
المعادلة
الثانية ثلثي محمد +
ثلاثة أرباع صالح = 340
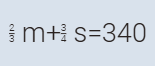 # 2
# 2
بطرح #2
من #1
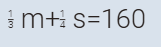 #3
#3
بضرب #3
في اثنين لوجود ثلثين في المعادلة #2
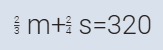 # 4
# 4
بطرح
# 4 من #2
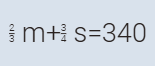 # 2
# 2
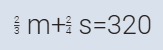 # 4
# 4
ينتج

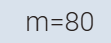
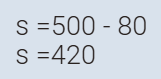
محمد
= 80 ثلثا محمد
ثلثا
ما مع صالح =280
و
ثلاثة أرباع ما مع محمد = 60 ريال
استراتيجية النمذجة الرياضية
( Mathematical Modeling )
مجموع
ما مع محمد وصالح 500 ريال . فاذا كان ثلثا ما مع صالح
و ثلاثة أرباع ما مع
محمد340 ريال .
فكم
ريال مع كل منهما
؟
المعادلة الأولى محمد +
صالح = 500
ثلثا صالح +ثلاثة أرباع محمد
= 340
نكمل الحل
استراتيجية التمثيل البصري
(Visual Representation )
في
المسألة :
ثلثا صالح
من أجل
ذلك نمثل محمد ب ثلاث مربعات بلون
 صالح
صالح
ثلاثة أرباع صالح
من أجل
ذلك نمثل صالح بأربع مربعات بلون مختلف
 محمد
محمد
محمد +
صالح = 500
 +
+
 = 500
( 1 )
= 500
( 1 )
ثلثي
صالح + ثلاثة أرباع
محمد= 340
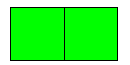 +
+
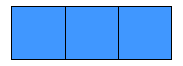 = 340
( 2 )
= 340
( 2 )
بطرح
( 2 ) من ( 1 ) نحصل على
 +
+ = 160
( 3 )
= 160
( 3 )
لوجود 3
مربعات من كل لون في (1) نضرب المعادلة ثلاثة في 3
فنحصل على
بالتعويض
بقيمة ( 3 ) في المعادلة ( 1 )
كالتالي :
 (
1 )
(
1 )
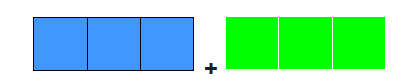 = 480
( 4 )
= 480
( 4 )
بطرح
المعادلة 4 من المعادلة 1 نحصل على
 =
20
=
20
 = 80
= 80
محمد= 80
صالح =
500 ناقص 80= 420
من
الممكن حل السؤال باستراتيجية بناء جدول
استراتيجية تبسيط المشكلة
(Simplifying the Problem)
حل المشكلة بتبسيط الأعداد إلى حالات أصغر
وأسهل، ثم استخدام الحل المبسط للوصول
إلى حل المشكلة
الأصلية
نحل مسألة مشابهة لكنها أبسط، ثم نعمم الفكرة.
نشاط
ما مجموع
الخمسين عدد فردي
الأولى ؟
ما القاعدة التي تحكم هذا النظام ؟
لمن يعرف قاعدة مجموع الأعداد الفردية
الاستراتيجية المناسبة
استراتيجية
كتابة قاعدة أو قانون
(Writing a Rule/Formula)
حل المشكلة بتحديد قاعدة أو قانون رياضي عام يمثل
العلاقة بين الكميات، بحيث يمكن استخدامه لحل المشكلة
الحالية
أو مشكلات مشابهة مستقبلًا.
مجموع عدد من
الأعداد الفردية = مربع عددها
لمن لا يعرف هذه الاستراتيجية تكون
استراتيجية تبسيط المشكلة
هي الأنسب
(Simplifying the Problem)
تكمن
فكرة التبسيط في البحث عن أعداد فرية أقل من 50 لمعرفة الحل
مجموعها
يمكن
أن يكون الحل بأكثر من استراتيجية
:
استراتيجية بناء
جدول
|
المجموع |
الترتيب |
# |
|
1 |
1 |
1 |
|
4 |
3 |
2 |
|
9 |
5 |
3 |
|
16 |
7 |
4 |
|
25 |
9 |
5 |
|
ن تربيع |
|
ن |
اكتشاف
قاعدة نمط
من الجدول
كما يمكن حلها باستخدام :
استراتيجية التمثيل البصري
(Visual Representation )
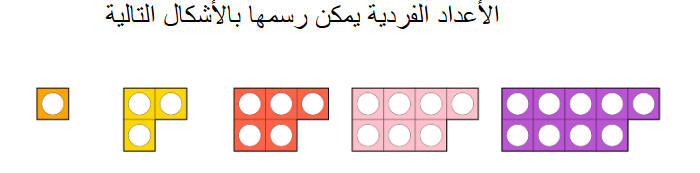
|
مساحة |
مجموع |
# |
|
واحد في واحد |
 |
1 |
|
اثنين في اثنين |
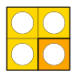 |
2 |
|
ثلاثة في ثلاثة |
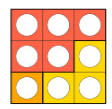 |
3 |
|
أربعة في أربعة |
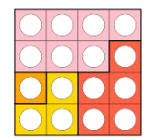 |
4 |
|
ن في ن |
|
ن
|
يمكن استخدام قاعدة
مجموع متوالية
نشاط
أعطى محمد لكل من أبنائه
سالم وصالح المبلغ نفسه .اشترى سالم 15 دفتر وبقي معه 15
ريال.
اشترى صالح 10 دفاتر وبقي
معه 35 ريال
فكم قيمة الدفتر؟
يمكن حل النشاط بعدد من
الستراتيجيات منها
- كتابة معادلة ( معادلة
واحدة)
- التخمين والتحقق
- بناء جدول
- الصور البصري
- كتابة معادلة ( معادلة
واحدة)
15د+15= د10+35
5د=20
د = 4 ريال
التخمين والتحقق
15دفتر+15 = سالم
10دفاتر+35=
صالح
تخمين
قيمة الدفتر 3 ريال
|
التساوي |
المجموع |
الباقي
|
دفاترصالح 10 |
المجموع |
الباقي |
دفاتر سالم |
|
لا |
65 |
35 |
30 |
60 |
15 |
45 |
- بناء جدول
15دفتر+15 = سالم
10دفاتر+35=
صالح
|
التساوي |
كتب صالح +35 |
كتب صالح |
كتب سالم +15 |
كتب سالم |
قيمة الكتاب
|
|
لا |
55 |
20 |
45 |
30 |
2 |
|
لا |
65 |
30 |
60 |
45 |
3 |
|
نعم |
75 |
40 |
75 |
60 |
4 |
- الصور البصري
15دفتر+15 = سالم
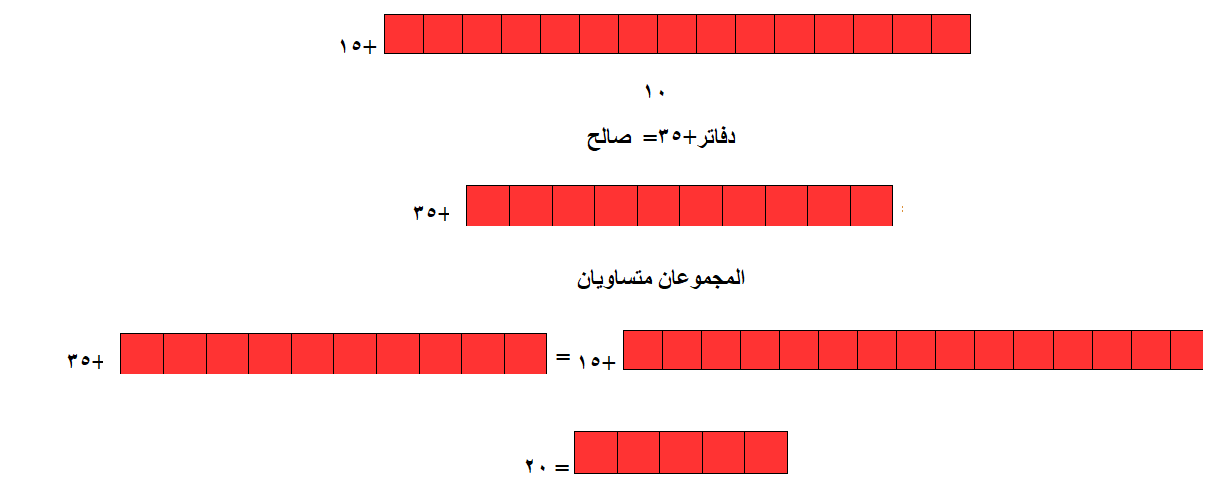
الدفتر= 4 ريال
استراتيجية التجربة المنظمة
(Systematic Trial)
حل المشكلة بتجربة جميع الاحتمالات بطريقة منظمة لضمان
العثور
على الحل الصحيح
دون إغفال أي خيار
نكتب جميع الاحتمالات
الممكنة بطريقة منظمة دون تكرار.
نشاط
تقابل 5 أشخاص في مطعم فاذا
صافح كل منهم الآخر
فكم عدد المصافحات التي تمت ؟

الأول
والثاني الأول
والثالث الأول والرابع
الأول والخامس
(1,2) , (1,3) , (1,4) ,(1,5)
(2,3) , (2,4) (2,5)
(3,4) ,(3,5)
(4,5)
|
الخامس |
الرابع |
الثالث |
الثاني |
الأول |
|
 |
 |
 |
 |
 |
|
4 |
3 |
2 |
1 |
|
|
7 |
6 |
5 |
 |
|
|
9 |
8 |
 |
|
|
|
10 |
 |
|
|
|
عدد
الأشخاص = 5
عدد
المصافحات = 10
ما القاعدة العامة اذا كان العدد
ن ؟
يوجد
العديد من المشكلات الرياضية التي يمكن حلها بأكثر من استراتيجة
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع
مامعهما معا
يساوي 120 ريال
فكم
ريال مع كل منهما ؟
ما
الاستراتيجيات الممكنة ؟
الاستراتيجيات الممكنة:
1- التخمين
والتحقق
2-
تبسيط المسألة بجعل النسبة بينهما النصف أو الثلث
3- كتابة
معادلة
4- التمثيل
بالرسم
5- التمثيل
بالنماذج ( مربعات أو مكعبات )
استراتيجية النمذجة الرياضية
( Mathematical Modeling )
تمثيل المشكلة رياضيًا باستخدام معادلات متعددة أو
رموز لتوضيح العلاقات بين الكميات، بهدف فهم المشكلة
وحلها رياضياً
نشاط
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع
مامعهما معا يساوي 120 ريال
فكم
ريال مع كل منهما
؟
ما مع محمد =
m
ما مع صالح =
s
#1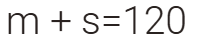
بالضرب في اثنين
2#
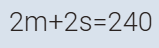
#3
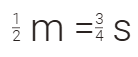
بضرب الطرفين في الوسطين والتبسيط نحصل على
# 4
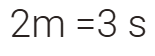
نعوض
من #4 في #2
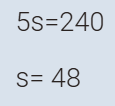
m=72
استراتيجية التمثيل البصري
(Visual Representation )
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع
مامعهما معا يساوي 120 ريال
فكم
ريال
مع كل منهما ؟

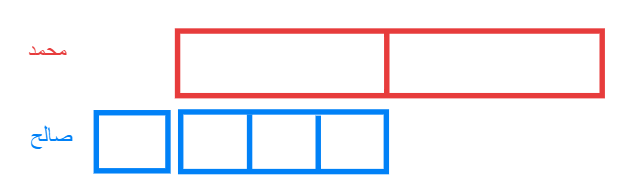
نصف ما مع محمد يساوي ثلاثة أرباع ما مع
صالح
نقسم نصف ما
مع صالح الى 3 أجزاء ليتساوى مع ثلاثة أرباع ما مع صالح
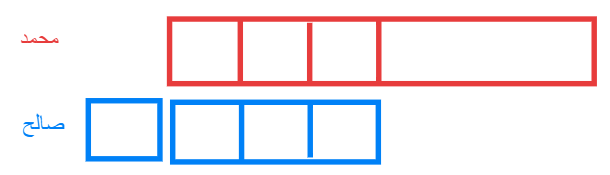
عدد المربعات
10 تساوي 120 ريال كل مربع =12 ريال
ما مع صالح = 48 ريال
ما مع
محمد 72 ريال
نشاط
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع
مامعهما معا
يساوي 120 ريال فكم
ريال
مع كل منهما ؟
أولا: حساب
النسبة بين ما مع محمد الى ما مع صالح

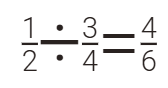
ثانيا :
نستخدم مكعبات
او مربعات لتمثيل ما مع كل منهما وفق النسبة
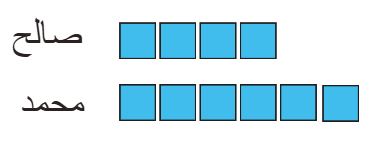
عشر
مربعات =120
المربع
الواحد =12
محمد = 72
صالح = 48
التأكد
نصف ما مع محمد =36
ثلاثة
أرباع ما مع صالح = 36
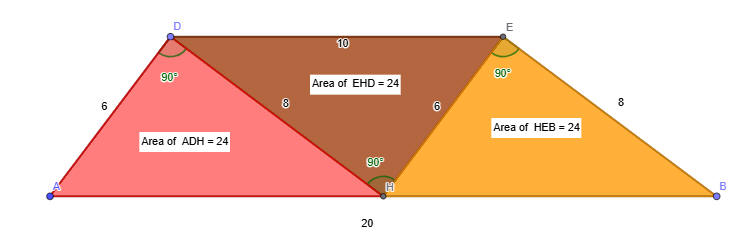
احسب مساحة شبه المنحرف
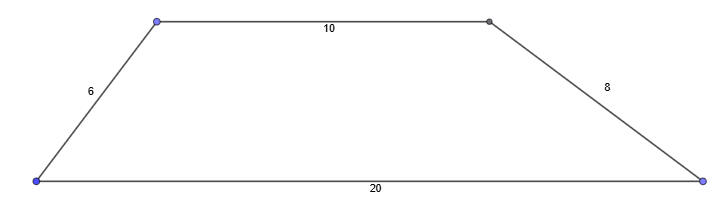
طبق نظرية فيثاغورث على المثلثين لحساب الارتفاع
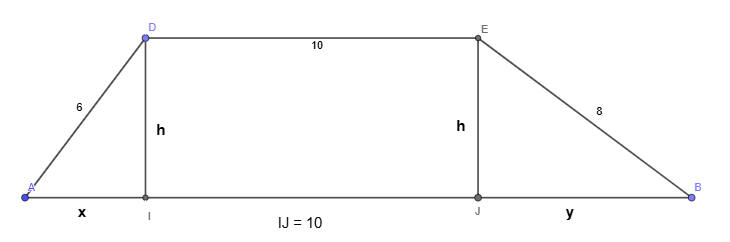
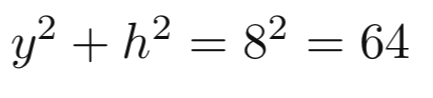
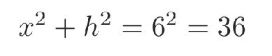
بالطرح
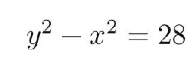
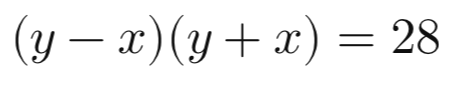
وحيث ان
x + y = 10
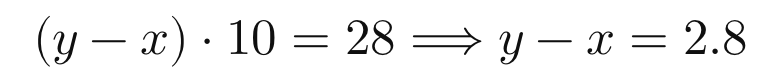
وحيث ان
x + y = 10
يكون
y = 6.4
x = 3.6
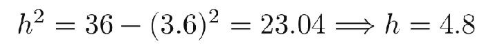
مساحة شبه المنحرف
نصف مجموع القاعدتين ضرب h
72 سم مربع
حل آخر
نصف القاعدة الكبرى ثم صل طرفي القاعدة الصغرى بنقطة المنتصف
نشاط
يبين الشكل أدناه 16
مربعا صغيرا و
9 مربعات كبيرة
ما الكسر الذي يمثله الجزء الملون من كامل
الشكل؟
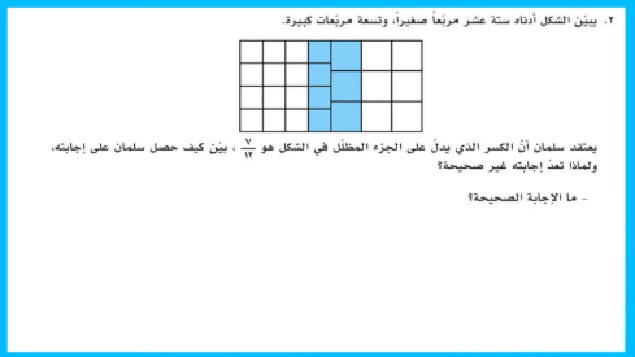
الشكل
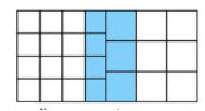
كل مربع = نصف الشكل الأساسي
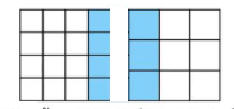
المربع الأيمن = نصف الشكل
تم تلوين ثلثه أي سدس الشكل الكلي
بالطريقة نفسها
المربع الأيسر=نصف الشكل
تم تلوين ربعه أي ثمن الشكل
الجزء الملون بالنسبة للشكل كامل يساوي
سدس+ثمن = 7 من 24
رابط
معادلات ax+by=c
أنشطة اضافية محلولة

















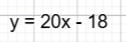








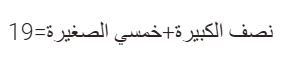

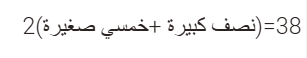















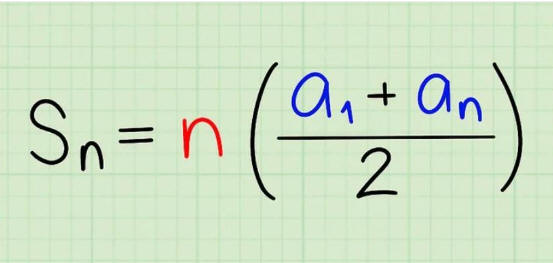







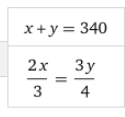












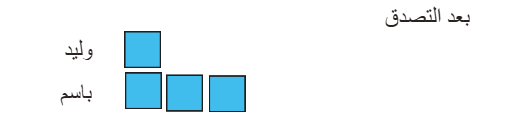


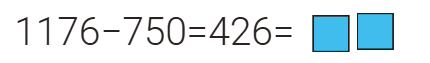
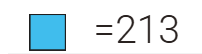
























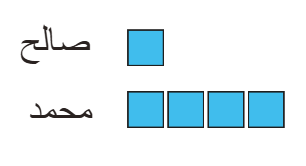


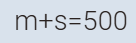 #1
#1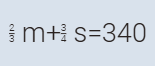 # 2
# 2
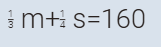
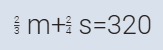

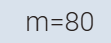
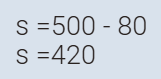
 صالح
صالح محمد
محمد
 = 500
( 1 )
= 500
( 1 )
 = 340
( 2 )
= 340
( 2 )
 = 160
( 3 )
= 160
( 3 )