نشاط 1
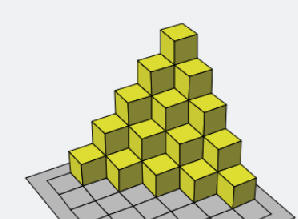
أي الصورتين أكثر وضوحا ؟
من كم طابق يتكون الشكل ؟
كم مكعب في كل طابق ؟
كم مجموع المكعبات في الشكل؟
كم مكعب تحتاج لبناء مماثل مكون من 10 طوابق؟
ماذا تحتاج للاجابة عن تلك الأسئلة؟
برمجية الرسم
https://aghandoura.com/SITE/3D/new_page_1.htm
applet9
مزيد من النماذج على الرابط
https://aghandoura.com/SITE/total/T.htm
المتتالية من الدرجة الأولى ومن الدرجة الثانية دينز
https://aghandoura.com/SITE/RULE/RULE.htm
المتتاليات و الأنماط
https://aghandoura.com/METEEBNEWNEW/LEVELS.htm
https://aghandoura.com/2030/APPLETS/Pattern%20BlocksNEW.htm
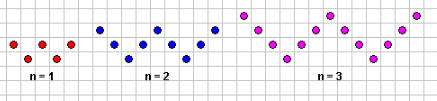
طاولة سداسية كم كرسي ؟
ماذا لوكانت طاولتان كم كرسي ؟
ما العلاقة التي تربط بين عدد الطاولات وعدد الكراسي
|
|
|
|
|
|
كم عدد الكراسي في حال عدد الطاولاات =100
ماذا لو كانت الطاولات عشارية الشكل (طاولة المستقلة 10حولها كراسي )
https://aghandoura.com/2030/APPLETS/CountersNEW.htm
|
|
|
|
|
|
ما العلاقة التي تربط بين عدد الطاولات وعدد الكراسي في حال كون الطاولات سداسية
لمعرفة العلاقة نبني جدول
| ط |
ك |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 5 | 22 |
| 6 | 26 |
| ن | ؟؟؟؟ |
مثل النقاط على شبكة مربعات
(1, 6) و (2 ,10) و ( 14,3)
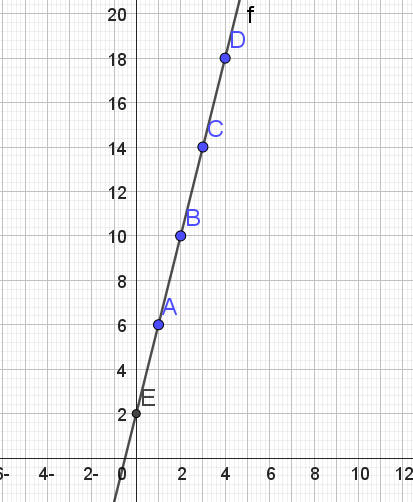
النقاط تمثل خط مستقيم
ميله 4 ويقطع محور الصادات عند 2
| ط |
ك | الفرق |
| 1 | 6 | |
| 2 | 10 | 4 |
| 3 | 14 | 4 |
| 4 | 18 | 4 |
| 5 | 22 | 4 |
| 6 | 26 | 4 |
| n | ؟؟؟؟ |
| الحد | القيمة |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 5 | 22 |
| 6 | 26 |
تمثل متتالية حدها الأول 6 والفرق 4
حسب قوانين المتتاليات
الحد العام يتم حسابه حسب المعادلة
=
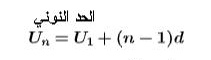
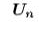الحد النوني
الحد الأول =
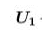
الفرق= d
الحد السادس في المتتالة السابقة
=
26
وهذا يتطلب معرفة الحد المطلوب ( العاشر مثلا )
وهناك قانون اخر لا يتطلب ذلك وانما التعويض مباشرة في المقدار
an+b
a= الفرق
لمعرفة قيمة b
نعوض في المقدار السابق
a+b= الحد الأول
الحد الأول =6
لحساب قيمة b
نعوض في المقدار
فيكون b=2
الحد العام
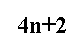
الحد السادس في المتتالة السابقة
n=6
an+b
a=4
a+b= الحد الأول
الحد الأول = 6
b=2
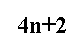
التأكد
| ط |
ك | الفرق |
| 6 | 26 | 4 |
===========================================================
التأكد من تساوي المقدارين
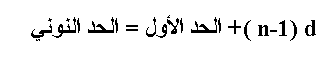
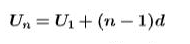
an+b
a=الفرق=d
an+b
dn+ b
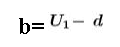
بالتعويض عن b وأخذ d عامل مشترك
an+b
=
=================================================================================
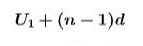
نشاط
مثل النقاط
| س |
ص | الفرق |
| 1 | 6 | 2 |
| 2 | 8 | 2 |
| 3 | 10 | 2 |
| 4 | 12 | 2 |
| 5 | 14 | 2 |
| 6 | 16 | 2 |
| n |
قم بتمثيل النقاط على شبكة تربيع
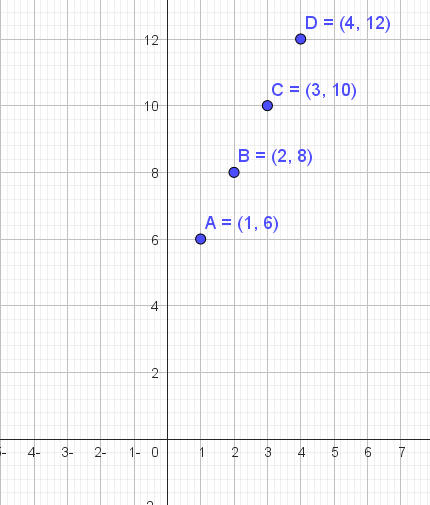
صل بين النقاط
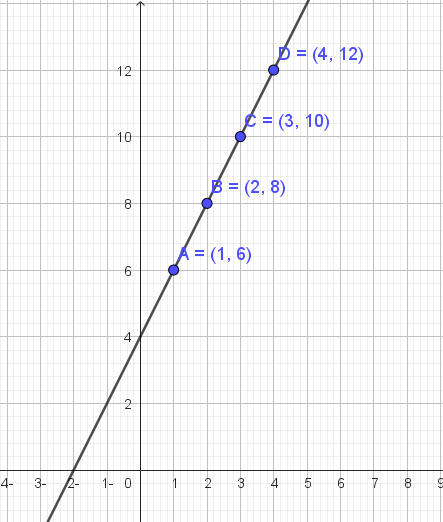
احسب ميل المستقيم = الفرق = الميل
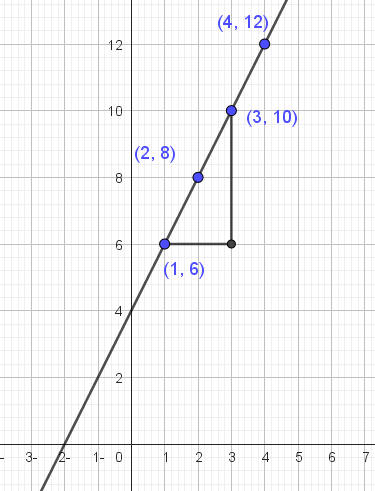
ما الجزء المقطوع من محور الصادات؟
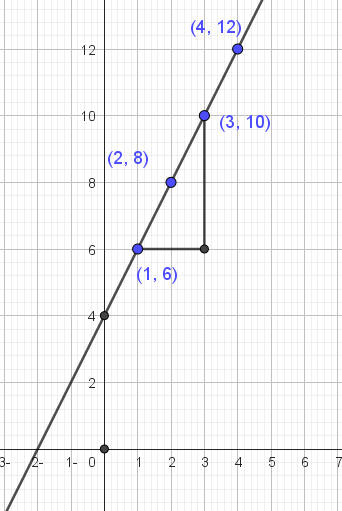
معادلة الخط المستقيم في صورة
an+b=y
a
الميل = الفرق
b
=
الحد الأول - الفرق
الجزء المقطوع من محور الصادات
a+b= الحد الأول
a=2
a+b=الحد الأول
الحد الأول =6
a+b=6
b=4
الحد النوني
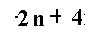
| س |
ص |
| 1 | 6 |
| 2 | 8 |
| 3 | 10 |
| 4 | 12 |
| 5 | 14 |
| 6 | 16 |
| n | 2ن +4 |
الحد السادس
=
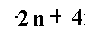
16
=====================================================================
برمجية أعواد الكبريت
http://thewessens.net/ClassroomApps/Main/matchsticks.html?topic=algebra&id=5
حلول أعواد الكبيريت
https://aghandoura.com/SAMYAH/ANMAT/ANMAT.html
حلول النقاط
https://aghandoura.com/METEEBNEWNEW/LEVELS.htm
برمجية الأنماط الجديدة
https://aghandoura.com/SIGMA/PAT.html
برمجية الطاولات
https://www.transum.org/Maths/Activity/Matchstick_Patterns/?Level=2
=====================================================================
هناك العديد من البرمجيات التي تعطي متتاليات من هذا النوع وتعطى الحد العام لكل متتالية
رابط البرمجية
https://aghandoura.com/GAMES/DBLOCKS/Dienes%20Blocks.htm
ويمكن التحكم في مستوى الصعوبة واختيار اظهار الحل
ادرس الجدول للتعرف على العلاقة بين بين مكوناته
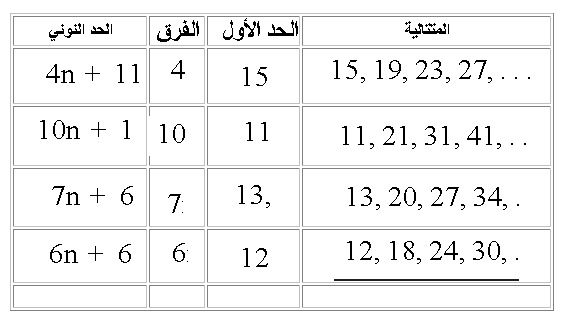
هل لاحظت العلاقة بين معامل n والفرق؟
معامل n = الفرق
هل لاحظت العلاقة بين الحدالنوني و الفرق والحد الأول
هللاحظت ان البرمجية تعرض لك العديد من الأمثلة دون السماح باختيار كتابة متتالية ؟
يوجد برمجية أخرى تسمح لك ببناء متتالية حسابية من اختيارك وتعطي الجد العام والمجموع أيضا
https://aghandoura.com/SITE/newsequnce.htm
=================================================================================================
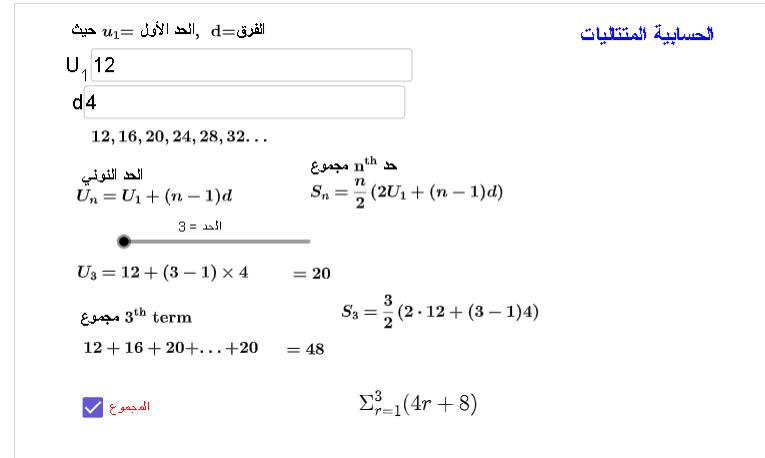
المتتالية
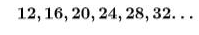
حدها الأول 12
الفرق 4
الحد العام
an+b
a= الفرق
b
=
الحدالأول ناقص الفرق
حسب قاعدة المتتاليات
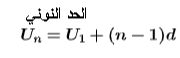
d= الفرق
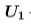= الحد الأول
الحد النوني
an+b
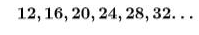
حدها النوني
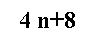
الحد السادس = 32
يساوي حدها النوني من قانون المتتاليات
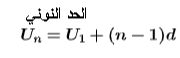
الحد الأول 12 الحد 6
الحد العام
12+5*4=32
===================================================
مجموع متتالية حسابية
من قانون المتتاليات المجموع يتم حسابه بالمعادلة
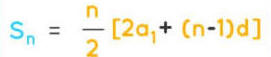
فالمتتالية
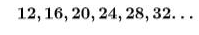
حدهها الأول 12 والفرق 4
مجموع الحدود الستة الأولى يساوي
================================================================
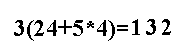
يمكن حساب مجموع المتتالية الحسابية من قوانين المجموع
الحد العام للمتتالية
لحساب مجموع الستة حدود الأولى نستخدم قوانين المجموع
مجموع الأعداد المتتالية
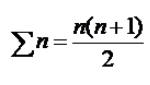
https://aghandoura.com/SITE/ADEL/Natural%20Numbers.html
مجموع من واحد الى ستة
=
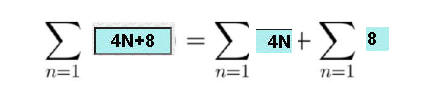
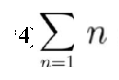= 84
+
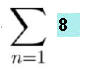= 48
المجموع يساوي
==========================================================================================
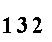
أكمل الجدول
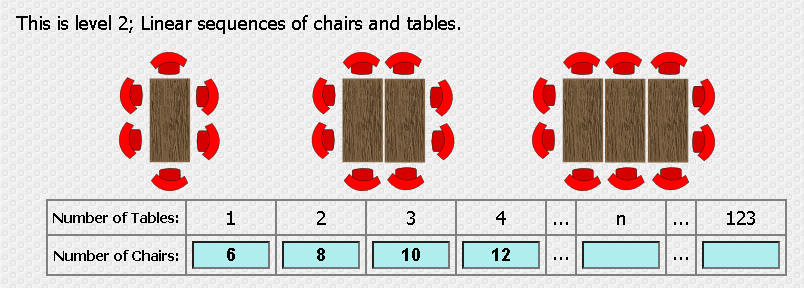
ما العلاقة بين عدد الطاولات وعدد الكراسي
أكمل
6 8 10 12 ---- ----
ما القاعدة التي تحدد قيمةn
متتالة حسابية حدها الأول 6 والفرق الثابت 2
الحد النوني من قانون المتتاليات
الحد الأول + ( ن-1) الفرق الثابت
الحد الرابع ن=4
الرابع = 6 + 3 (2)
الرابع = 12
ن=؟
الحد النوني بموجب الفروق يتم حسابه من المقدار
an+b
الفرق بين حدين متتالين =a
الحد الأول = a+b
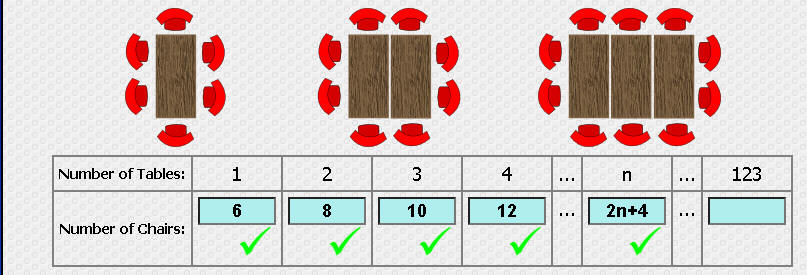
الحد 123= 2(123) +4
246+4=250
ما القاعدة ؟
6 8 10 12 ---- ----
نحسب الفرق بين كل حدين متتالين
6 8 10 12 ---- ----
الفرق الثابت = 2
الحد العام في صورة
an+b
الفرق الثابت في المتتالية = 2
a+b= الحد الأول = 6
نسحب قيمة b
a+b=6
b=4
an+b
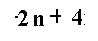
الحد الثالث = 10
التأكد
ويمكن حساب المجموع بالطريقة السابقة
=========================================================================
حساب الحد النوني في المتتاليات من الدرجة الثانية
=========================================================================
هل لاحظت أن الأمثلة في البرمجيات السابقة
تعطي متتاليات يكون فيها الفرق بين حدين متتالين ثابت ؟
في بعض الأوقات لايكون الفرق ثابت بين حدين متتالين مثل
برمجية النقاط بصورة محسوسة
https://aghandoura.com/METEEBNEWNEW/LEVELS.htm
أو بصورة مجردة
في البرمجية
https://aghandoura.com/GAMES/DBLOCKS/Dienes%20Blocks.htm
مثال
تعطي متتاليات لايكون فيها الفرق بين حدين متتالين ثابت وفي الوقت نفسه تعطي الحد النوني
فكيف يمكن حساب الحد العام لهذا النوع من المتتاليات ؟
لعلك لاحظت أن الفرق بين حدين متتالين ليس ثابت من المرة الأولى
ولكنه يثبت في المرة الثانية لذك الحد العام لها هو من الدرجة الثانية
فكيف يمكن حساب الحد العام لهذا النوع من المتتاليات ؟
الحد العام في صيغة
an^2+bn+c
مثال
https://aghandoura.com/SAMYAH/ANMAT/FOUR.pdf
وقيمة a b c تحدد بالتالي
الفرق الثاني = 2a
الفرق الأول =3a+b
الحد الأول = a+b+c
المتتالية
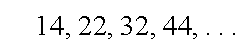
حدها الأول
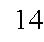
الفرق الأول = 8
المتتالية بعد الفرق الأول تصبح
8 10 12 14 16
الفرق الثاني
2 2 2 2 2
حسب القواعد السابقة التي باللون الأحمر
الفرق الثاني = 2a
2a=2
a=1
الفرق الأول =3a+b
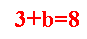
b=5
الحد الأول = a+b+c
الحد الأول = 14
c=8
an^2+bn+c
الحد العام للمتتالية
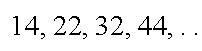
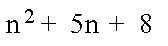
حدها الرابع 44 يمكن حسابه من القاعدة
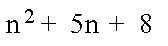
بالتعويض
n=4
16+20+8=44
==========================================================================================
الخلاصة
عندما يكون الفرق الثاني هو الفرق الثابت نعوض في التالي
an^2+bn+c
2a= الفرق الثابت
3a+b=الفرق الأول
a+b+c= الحد الأول
=================================================================
https://aghandoura.com/SITE/total/T.htm
من كم طابق يتكون الشكل ؟
كم عدد المكعبات أسفل الشكل ؟
كم عدد المكعبات في الطابق الأوسط ؟
كم مجموع المكعبات كاملة ؟
========================================================================
حساب مجموع المتتاليات التي من الدرجة الثانية
==========================================
المتتالية
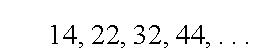
من الدرجة الثانية
حدها العام
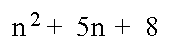
لحساب مجموعها نحسب مجموع حدود الحد العام
الهدف هوالوصول الى الحل بسرعة والتأكد من صحة الحل
التحدي يصنع الإبداع
================================================
نشاط من الحياة
حصالة فيها ألف ريال قرر محمد أن يأخذ كل يوم 17 ريال زيادة عن اليوم السابق فكم يبقى في الحصالة
بعد سحب اليوم العاشر؟
ما القاعدة التي تحدد المبلغ الباقي؟
الحالة الأولى يكون فيها مقدار السحب الأول = الزيادة اليومية
المقدار الأول 17 والزيادة اليومية نفس المبلغ
|
قانون مجموع الأعداد المتتالية بصفة عامة إذا كان المبلغ المسحوب في أول مرة يساوي مبلغ الزيادة اليومية فإن مجموع المبلغ المسحوب لعدد محدد من الأيام تحكمه هذه الصيغة
n = عدد الأيام |
الحل بطريقة المتتاليات
يمكن بناء جدول يربط رقم اليوم والمبلغ
المبلغ الأساس 1000 ريال
من هذا الجدول
| اليوم | المبلغ | المبلغ | ||
| 1 | 17 | 1 | في | 17 |
| 2 | 34 | 2 | في | 34 |
| 3 | 51 | 3 | في | 51 |
| 4 | 68 | 4 | في | 68 |
| 5 | 85 | 5 | في | 85 |
| 6 | 102 | 6 | في | 102 |
| 7 | 119 | 7 | في | 119 |
| 8 | 136 | 8 | في | 136 |
| 9 | 153 | 9 | في | 153 |
| 10 | 170 | 10 | في | 170 |
القاعدة التي تربط المبلغ ليوم محدد هي رقم اليوم ضرب 17
لمعرفة مجموع ما تم سحبه نكمل الجدول
| اليوم | المبلغ | الجموع |
| 1 | 17 | 17 |
| 2 | 34 | 51 |
| 3 | 51 | 102 |
| 4 | 68 | 170 |
| 5 | 85 | 255 |
| 6 | 102 | 357 |
| 7 | 119 | 476 |
| 8 | 136 | 612 |
| 9 | 153 | 765 |
| 10 | 170 | 935 |
| الباقي | 65 | |
الحد الأول = 17
الحد الأخير =170
عدد الأيام= 10
القاعدة
المجموع يساوي
نصف عدد الأيام ( الأول +الأخير)
5(17+170) = 5 (187)= 935
الباقي في الحصالة 1000 ناقص 935
65 ريال
|
قانون مجموع متتالية بصفة عامة إذا كان المبلغ المسحوب في أول مرة يساوي مبلغ الزيادة اليومية فإن مجموع المبلغ المسحوب في عدد محدد من الأيام تحكمه هذه الصيغة ( نصف عدد الأيام ) ( الحد الأول + الحد الأخير )
|
نشاط :
المبلغ الموجود في الحصالة 4300 ريال اول يوم سحب 20 ريال واليوم الثاني يسحب 20 زيادة عن اليوم السابق واليوم الثالث يسحب 20 زيادة اي 60
ريال وهكذا لمدة 20 يوم ما المبلغ المتبقي في الحصالة ؟
نبني الجدول
| اليوم | المبلغ |
| 1 | 20 |
| 2 | 40 |
| 3 | 60 |
| 4 | 80 |
| ن | 20 ن |
مجموع المبلغ المسحوب لعدد محدد من الأيام تحكمه هذه الصيغة
|
قانون مجموع الأعداد المتتالية بصفة عامة إذا كان المبلغ المسحوب في أول مرة يساوي مبلغ الزيادة اليومية فإن مجموع المبلغ المسحوب في عدد محدد من الأيام تحكمه هذه الصيغة
n = عدد الأيام
|
مجموع المبالغ المسحوبة في 20 يوم
=
20(20) (21)/2= 4200 ريال
الباقي 100 ريال
===========================================
طريقة المتتاليات
عدد الأيام 20
اليوم الأول = 20
اليوم رقم 20 =400
المجموع
نصف عدد الأيام = 10
الأول + الأخير=420
المجموع= 420 ضرب 10= 4200
===============================================================================
ماذا لو اختلف المبلغ المسحوب عن الزيادة اليومية
مثال
المبلغ في الحصالة 500 ريال يسحب أول يوم 20 ريال والزيادة اليومية 5 عن اليوم الذي قبله
المدة عشرة أيام
يسحب أول يوم 20 ريال والزيادة اليومية 5 عن اليوم الذي قبله
20 25 30 35 40 45 ....
| اليوم | المبلغ | الفرق | القاعدة ليوم محدد
|
| 1 | 20 | 5 | 5n+15 |
| 2 | 25 | ||
| 3 | 30 | 5 | |
| 4 | 35 | 5 | |
| 5 | 40 | 5 | |
| 6 | 45 | 5 | |
| 7 | 50 | 5 | |
| 8 | 55 | 5 | |
| 9 | 60 | 5 | |
| 10 | 65 | 5 | |
| الباقي | |||
القاعدة التي تحدد السحب في يوم محدد هي
5n+15
الحد الأول - الفرق =15
المجموع بطريقة مجموع الأعداد المتتالية
مجموع 5n
+
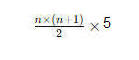
مجموع 15 لعدد الأيام
عدد الأيام =10
10x11x 5 /2 =275
+
مجموع 15 لعدد الأيام
150
275+150=425
التأكد
لحساب المجموع الكلي نبني جدول
| اليوم | المبلغ | المجموع | القاعدة
مجموع 5n+15
+ 150 |
| 1 | 20 | 20 | |
| 2 | 25 | 45 | |
| 3 | 30 | 75 | |
| 4 | 35 | 110 | |
| 5 | 40 | 150 | |
| 6 | 45 | 195 | |
| 7 | 50 | 245 |
10(11)5 /2= 275 + 150 = 425 |
| 8 | 55 | 300 | |
| 9 | 60 | 360 | |
| 10 | 65 | 425 | |
|
الباقي |
75 | ||
المجموع لعدد محدد من الأيام = مجموع المقدار
+
10(15)
يساوي
=
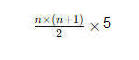5(10)(11)/2=275
+
150
=425
===================================================================================
الحل بطريقة المتتاليات
الحد الأول 20
المدة = 10
قانون الحدود
5n+15
الحد الأخير = 65
المجموع
نصف عدد الحدود =5
الأول + الأخير= 85
القانون
نصف عدد الحدود ( الأول + الأخير )
425= 5 85x
نشاط 2
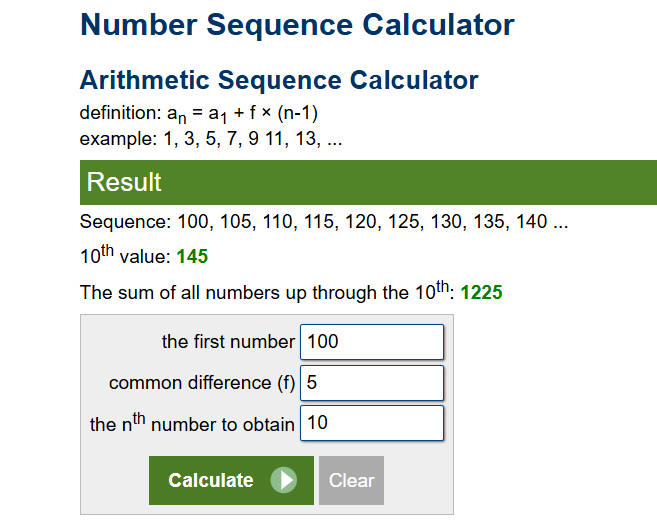
في هذا الشهرقرر محمد أن يضع 100 ريال في حصالته الشخصية , وأن يضع بعد ذلك كل شهر 5 ريال زيادة عن الشهرالذي قبله.
فكم المبلغ الذي يضعه في الشهر العاشر وما المبلغ الموجود في الحصالة بعد ايداعه الشهر العاشر ؟
| الشهر | المبلغ | الفرق | المجموع |
| الشهر الأول | 100 | 5 | 100 |
| الشهر الثاني | 105 | 205 | |
| الشهر الثالث | 110 | 5 | 315 |
| الشهر الرابع | 115 | 5 | 430 |
|
الشهر الخامس |
120 | 5 | 550 |
| الشهر السادس | 125 | 5 | 675 |
| الشهر السابع | 130 | 5 | 805 |
| الشهر الثامن | 135 | 5 | 940 |
| الشهر التاسع | 140 | 5 | 1080 |
| الشهر العاشر | 145 | 5 | 1225 |
| ---------- | ------- |
--------- |
|
|
--------- |
------ |
--------- |
طريقة أخرى :
100 105 110 115 120 ---- ----
يمكن تمثيل الوضع في صورة أزواج مرتبة
Y X 100 1 105 2 110 3 106 4 ------ ----- ------
------
------
الأزواج المرتبة تمثل خط مستقيم
معادلة الخط المستقيم
Y=ax+b
الميل = a
b =الجزء المقطوع من محور الصاات
الميل = 95
| Y | X |
| 100 | 1 |
الميل
y-x= 5
Y=5X+b
b=95
الحد النون 5x+95
Y=5X+95
اليوم العاشر يضع
145
=====================================================
الطريقة المعتادة
هذه الحالة تمثل متتالية حسابية حدها الأول 100 ومقدار الزيادة 5
الحد النوني
an = a + (n - 1)d
a= الحد الأول
d= الفرق الثابت
n= رتبة الحد
الحد العاشر
a10 = 100 + (10 - 1)5
145
| الشهر العاشر | 145 |
-----------------------------------------
لحساب المجموع نحسب مجموع الحد النوني
5x+95
مج 5x من واحد الى 10 وكذلك مج 95 عشر مرات
لمعرفة مجموع متتالية حسابية نستخدم القانون
البرمجية
