متتاليات الدرجة الأولى والدرجة الثانية
البرمجية
https://aghandoura.com/GAMES/DBLOCKS/Dienes%20Blocks.htm

نختار

من القائمة المنسدلة

نختار رقم 23

اظهار الحل


الحد الأول = 7
الفرق= 4
مثال جديد

هل لاحظت أن الحل في صورة
an+b
الحد الأول =15
الفرق= 10
من خلال العديد من الأمثلة يكتشف الطالب قيمة a وقيمة b
العلاقة بين الحد الأول و قيمة a وقيمة b
ما العلاقة بين الفرق ومعامل n
| الحد الثابت | الفرق | الحد الأول | معامل n | الحد النوني | المتتالية |
 |
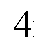 |
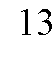 |
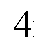 |
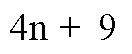 |
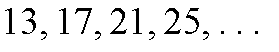 |
|
|
|
|
|
|
|
|
|
|
|
|
|
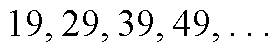 |
|
|
|
|
|
|
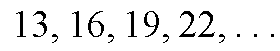 |
|
|
|
|
|
|
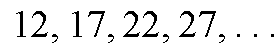 |
|
؟؟؟؟؟ |
|
|
؟؟؟؟؟ |
؟؟؟؟؟ |
|
هل لاحظت أن الحد الثابت يساوي الحد الأول ناقص الفرق ؟
لاحظت أن معامل n = الفرق بين أي حدين متتالين
a= الفرق بين حدين
b
يمكن حسابها من
a+b = الحد الأول
هذا هو قانون حساب الحد العام لجميع المتتاليات الحسابية
المتتالية
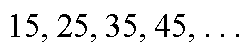
الفرق= 10
الحد الأول =15
حدها العام هو
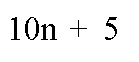
الحد الرابع
N=4
الحد الرابع =45
هو نفس القيمة اذا استخدمنا قانون الحد النوني لمتتالية حسابة
الحد النوني
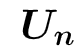
الحد الأول
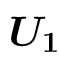
d= الفرق
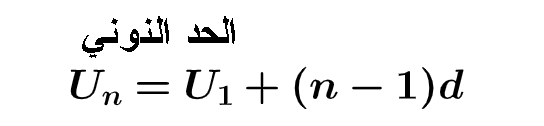
الحد الرابع n=4
15+3*10= 45
=========================================================================
لحساب مجموع متتالية حسابية توجد طريقتين
الأولى باستخدام قانون مجموع متتالية حسابية
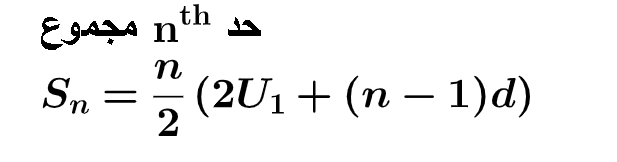
احسب مجموع الأربعة حدود الأولى من المتتالية
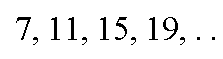
d = الفرق بين حدين متتالين = 4
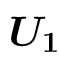 = الحد الأول
= 7
= الحد الأول
= 7
بالتعويض في القانون
نصف عدد الحدود (14+(4-1)4
=
2(14+12) = 52
المجموع = 52 للحدود الأربعة الأولى
7+11+15+19= 52
==================================================
الطريقة الثانية بتطبيق قانون مجموع الأعداد المتتالية
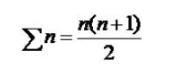
نطبق القانون على الحد العام للمتتالية مرة على المقدار الأول من الحد العام للمتتالية
ومرة ثانية على المقدار الثاني من الحد العام للمتتالية
المتتالية
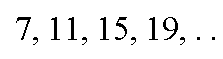
حدها العام
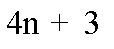
مجموع حدودها الأربعة = 52
7+11+15+19= 52
نستخدم قانون مجموع الأعداد المتتالية
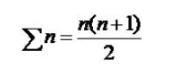
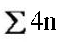
تساوي
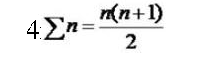
من واحد الى 4 = 40
+
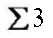
من واحد الى4= 12
المجموع = 52
===============================================================
حساب الحد العام للمتتاليات التي من الدرجة الثانية
9 20 35 54 77 ......
متتالية من الدرجة الثانية لأن الفرق بين أي حدين غير ثابت
الصيغة العامة لها هي
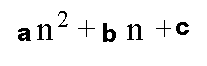
نكمل الجدول
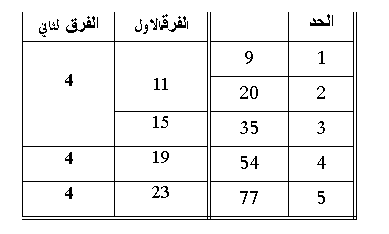
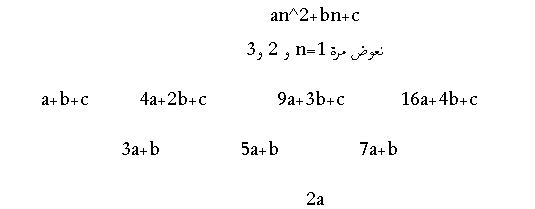
الفرق الثاني = 4
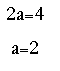
الفرق الأول = 11
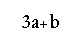 =
11
=
11
b=5
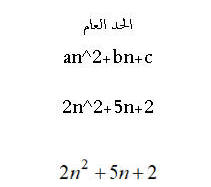
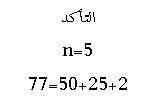
===============================================================
متتاليات الدرجة الثانية

من القائمة المنسدلة اختر رقم 23

المتتالية
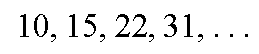
|
الحد |
القيمة | الفرق 1 | ف2 |
| 1 | 10 | 5 | 2 |
| 2 | 15 | ||
| 3 | 22 | 7 | |
| 4 | 31 | 9 | 2 |
| n |
الفرق الأول =5
بعد الفرق الأول تصبح المتتالية
5 7 9 11 .....
الفرق الثاني = 2
الحد الأول = 10
الحد العام في صورة
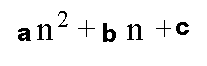
طريقة حساب الحد العام
نحسب الفرق الأول
نحسب الفرق الثاني
الفرق الثاني = 2a
الفرق الأول = 3a+b
الحد الأول = a+b+c
a= 1
الفرق الأول =5
3a+b= 5
b=2
الحد الأول = 10
a+b+c= 10
c=7
الحد العام
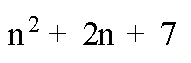
الحد الرابع
16+8+7= 31
=================================================
حساب مجموع متتالية من الدرجة الثانية
أولا نحسب الحد العام للمتتالية
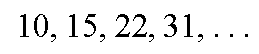
|
الحد |
القيمة | الفرق 1 | ف2 |
| 1 | 10 | 5 | 2 |
| 2 | 15 | ||
| 3 | 22 | 7 | |
| 4 | 31 | 9 | 2 |
| n |
الفرق الثاني =2
2a=2
a=1
الفرق الأول = 5
3a+b= 5
b=2
الحد الأول = 10
a+b+c= 10
c=7
الحد العام
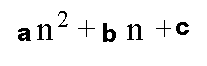
الحد العام
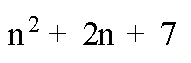
الحد الرابع للمتتالية
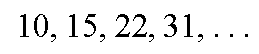
31
بالتعويض في المقدار
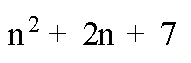
ب n=4
16+2*4+7= 31
=========================================================
ثانيا نطبق قانون المجموع على الحد العام للمتتالية
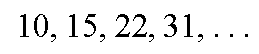
حدها العام
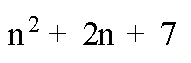
نطبق قانون
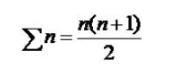
على الحد الأخير وعلى الحد الأوسط
الحد الأوسط
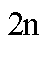
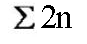
يساوي
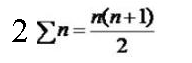
الحد الثابث =7
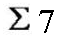
وقانون
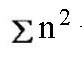
يساوي
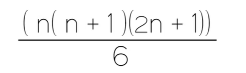
على الحد الأول
الحد العام
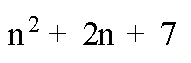
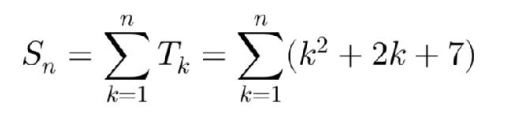
|
|
|
|
|
|
|
|
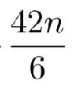 |
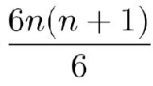 |
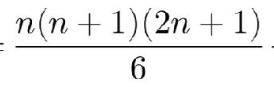 |
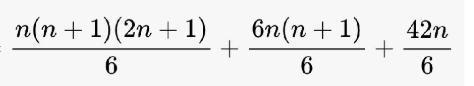 |
||
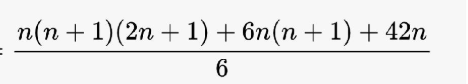 |
||
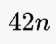 |
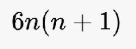 |
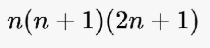 |
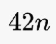 |
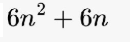 |
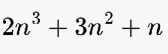 |
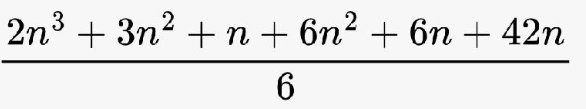 |
||
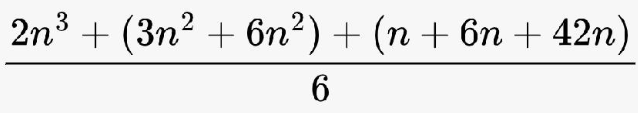 |
||
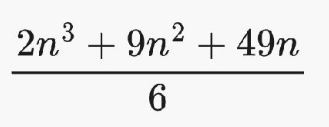 |
||
بعد تبسيط جميع المقادير
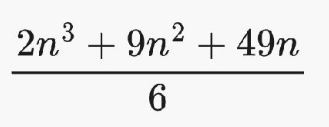
مجموع الأربع حدود الأولى من المتتالية
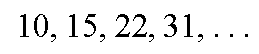
10+15+22+31= 78
========================================================
الطريقة الثانية لحساب مجموع متتالية من الدرجة الثانية
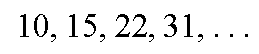
| الفرق3 | الفرق 2 | الفرق 1 | المجموع | المقدار | ت |
|
2 |
7 | 15 | 10 | 10 | 1 |
| 25 | 15 | 2 | |||
| 22 | 47 | 22 | 3 | ||
|
2 |
9 | 31 | 78 | 31 | 4 |
| 11 | 42 | 120 | 42 | 5 |
الحد العام من الدرجة الثالثة في صورة
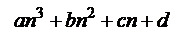
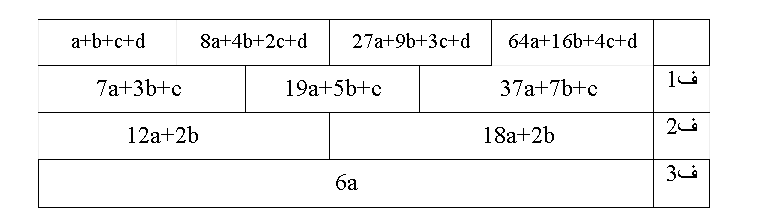
الفرق الثالث =
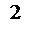
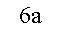 =
=

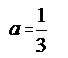
الفرق الثاني =
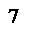
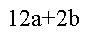 =
=
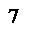
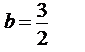
الفرق الأول =15
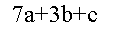
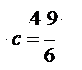
الحد الأول =10
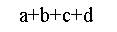 =
10
=
10
d=zero
بالتعويض في المقدار
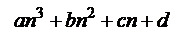
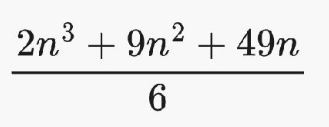
لحساب مجموع الأربع حدود الأولى من المتتالية
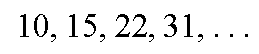
10+15+22+31= 78
128+144+176= 448
448 قسمة 6= 78
---------------------------------