
Describe the number of chairs needed with a formula.
This exercise will help you interpret mathematical relationships both algebraically and geometrically.
Close

Level 1 - Linear sequences of matchstick patterns
Level 2 - Linear sequences of chairs and tables
When you have done those why not progress to:
Sequences Level 2 - Find the nth term of linear sequences
Sequences Level 3 - Find a given term of linear sequences
Sequences Level 4 - Mixed questions about geometric sequences
Sequences Level 5 - Mixed questions about sequences and series
Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.
See the National Curriculum page for links to related online activities and resources.
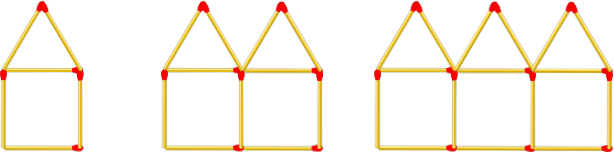
Filling in the first three cells of the table is simply a case of counting the number of matches needed to make the first three patterns.

You may have noticed by now how many additional matches it takes to make the next pattern in the sequence. It's the same each time you change one pattern to the next. In this case it is 5.
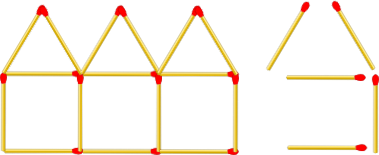

The numbers in the table go up by 5 each time just like the five times table. The general term of the five times table is 5n where n are the counting numbers (1, 2, 3, 4...).
The first four terms of the five times table are 5, 10, 15 and 20.
The numbers in our table are each one more than that so the nth term is 5n+1. This formula can be used to work out the 92nd term of the sequence i.e. 5x92+1 = 461

Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.
Close
