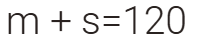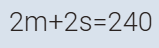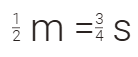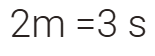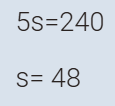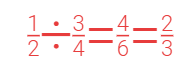استراتيجيات حل المشكلات الرياضية
1- استراتيجية التخمين والتحقق (Guess and Check)
2- استراتيجية بناء جدول (Make a Table)
3- استراتيجية البحث عن نمط (Look for a Pattern)
4- استراتيجية البدء من النهاية (Work Backward)
5- استراتيجية الرسم والتمثيل البصري (Draw a Diagram)
6- استراتيجية كتابة معادلة (Write an Equation)
7استراتيجية التبسيط (Simplify the Problem)
8- استراتيجية التمثيل بنماذج ومجسمات (Models or Manipulatives)
9- استراتيجية التجربة المنظمة (Systematic Listing)
10- استراتيجية تطبيق قاعدة أو قانون لحساب المطلوب ( قانون المتتاليات )
نشاط
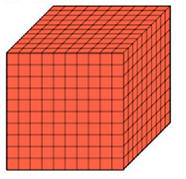
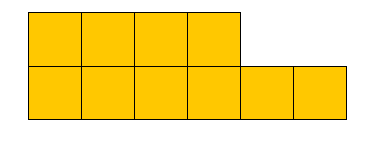
مصنع ثلج يمكنه انتاج 1000 مكعب طول ضلع الواحد منها يساوي1 سم .
اذا أراد أن ينتج مكعبات بطول 2 سم باستخدام نفس الكمية من الماء
فكم مكعب يمكنه أن ينتج ؟
كم عدد المكعبات 1x1
كم عدد المكعبات 2x2
نشاط
ما السؤال ؟
ما الاسترتيجة المناسبة ؟
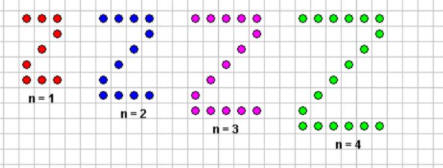
السؤال كم عدد النقاط في الشكل رقم خمسين؟
هل تفيد استراتيجية التخمين والتحقق ؟
استراتيجية بناء جدول
عدد النقاط
الشكل
9
1
12
2
15
3
18
4
21
5
هل ممكن استنتاج قاعدة ؟
الاستفادة من الفرق الثابت بين كل حدين متتاليين
الفرق
عدد النقاط
الشكل ----
9
1
3
12
2
3
15
3
3
18
4
3
21
5
الحل المقترح استخدام
قانون المتتاليات الحسابية
الحد النوني
an=a1+(n-1)d
d= الفرق بين حدين متتاليين
a1 = الحد الأول
n= رقم الحد
من الجدول نلاحظ ان الشكل الخامس فيه 21 نقطة
الفرق عدد النقاط
الشكل رقم 3 21
5 نطبق القانون
an=a1+(n-1)d
الحد الأول =9
الفرق=3
الحد الخامس = 9 +4(3)=21
قانون بديل وسريع ( اعادة كتابة القانون )
an=a1+(n-1)d
an=a1+nd- d
an=nd + a1- d
الحد المطلوب = ( الفرق x رقم الحد ) + ( الحد الأول - الفرق )
3ن + 6
الحد الخامس = 3(5) +6 =21
استراتيجيات حل المشكلات
1 : استراتيجية التخمين والتحقق (Guess and Check)
نخمن حلاً، ثم نتحقق إن كان يحقق الشروط، ونعدّل التخمين حتى نصل للحل الصحيح.
عددان مجموعهما 100، والفرق بينهما 50
ما العددان
• نخمن 60 و 40
الفرق 20
• نخمن 70 و 30
الفرق 40
نخمن 80 و 20
الفرق 60
نخمن 75 و 25
الفرق 50
العددان 75 و 25
الحل بطريقة ابداعية
ماالعددان اللذان مجموعهما 117 والفرق بينهما 17 ؟
تتلخص الطريقة في الخطوات التالية :
- طرح الفرق بين العددين
- قسمة باقي الطرح على 2 ينتج العدد الأصغر
المثال :
117 ناقص 17
يساوي 100
العدد الأصغر 100= قسمة 2
الأصغر= 50
العدد الأكبر = المجموع - الأصغر
الأكبر= 117- 50
67= الأكبر
مثال : أرض مستطيلة الشكل محيطها 500 وعرضها يساوي ربع طولها احسب مساحة الأرض
2استراتيجية بناء جدول (Make a Table)
الفكرة:تنظيم المعطيات في جدول يساعد على رؤية الحل بسهولة.
عددان مجموعهما 340 وثلثا أحدهما يساوي ثلاثة أرباع الآخر . فما هما العددان ؟
يمكن حل السؤال بأكثر من استراتيجية مثل :
التخمين والتحقق
كتابة معادلة
بناء جدول
بناء نموذج
*****************************************************************************
التخمين والتحقق
من المعطيات ثلثا أحدهما يساوي ثلاثة أرباع الآخر. وحيث ان الثلثين قريبة من الثلاثة أرباع يمكن التخمين أن العددين متساويان
أحدهما 170 والآخر 170 ونظرا لأن 170 لا تقبل القسمة على ثلاثة نختار 180 ونختبر ذلك التخمين . الأول 180 الآخر 160
ثلثا الأول 120 و ثلاثة أرباع الآخر 120 . وهما متساويان . وعليهما الأول 180 والآخر 160
بناء جدول
قبل بناء الجدول يجب دراسة المعطيات . أحد المعطيات ثلثا الأول تعني أن الأول يجب أن يكون قابل
للقسمة على ثلاثة .
الحالة الأول الثاني ثلثا الأول ثلاثة أرباع الثاني المساواة 1 150 190 100 142,5 لا 2 180 160 120 120 نعم 3
استراتيجية بناء نموذج
عددان مجموعهما 340 وثلثا أحدهما يساوي ثلاثة أرباع الآخر . فما هما العددان ؟
النسبة بين العددين
أحدهما 8 مربعات والآخر 9 مربعات
ثلاثة أرباع الثمانية= ثلثي التسعة
17 مربع= 340
المربع الواحد= 20
أحدهما 180
الآخر 160
استراتيجية تطبيق قاعدة أو قانون
بدأ محمد بالتوفير فقرر أن يضع في اليوم الأول 100 ريال . وفي كل يوم يضع خمس ريالات زيادة
عن اليوم السابق . فكم ريالا يجب عليه أن يضع في يومه الخامس.؟
الحد ن = الأول + الفرق ( ن -1)
أو
الحد المطلوب = ( الفرق x رقم الحد ) + ( الحد الأول - الفرق )
اليوم
المبلغ
الفرق
1
100
5 2
105
3
110
5 4
115
5
120
5 6
125
ن
العلاقة 5ن + 95
يمكن حساب العلاقة من الفرق ومبلغ اليوم الأول.
مبلغ اليوم الأول = 10
الفرق =5
العلاقة
ايداع يوم محدد يمكن حسابه بالعلاقة
الحد المطلوب = ( الفرق x رقم الحد ) + ( الحد الأول - الفرق )
ما قاعدة التسلسل؟
1,3,5,7,9,11
الحد الأول =1
الفرق= 2
الجدول
الحد
القيمة
الفرق
القاعدة
1
1 2
2ن - 1
2
3 3
5
2
4
7
5
9
2
6
11
ن
العاشر يعني ن= 10
الحد الأول =1
الأساس (الفرق) = 2
الحد ن = الأول + الفرق ( ن -1)
الحد العاشر = الأول + 2(10- 1)
الحد العاشر = 1 + 2(9)
الحد العاشر = 19
قيمة الحد ممكن معرفته بالعلاقة :
الحد المطلوب = ( الفرق x رقم الحد ) + ( الحد الأول - الفرق )
3 استراتيجية البحث عن نمط (Look for a Pattern)
الهدف :اكتشاف نمط تسلسلي في أعداد أو
أشكال للوصول إلى القاعدة العامة.
مثال على التسلسل في الأعداد
اكتشف قاعدة التسلسل
3 6 9 12 15 18 21 .....
نكتب النمط التسلسلي في الأعداد في جدول
للوصول إلى القاعدة العامة.
الجدول
الحد
القيمة
الفرق
القاعدة
1
3
3
3ن
2
6
3
9
3
4
12
5
15
3
6
18
ن
الحد المطلوب = ( الفرق x رقم الحد ) + ( الحد الأول - الفرق )
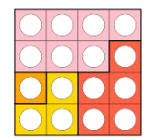
مثال على التسلسل في الأشكال
بالنظر الى الشكل نجد أنه يسير وفق نمط معين والهدف هو اكتشاف هذا النمط
النمط
1 ,3 ,6, 10 ,15 , .....
الاستعانة بجدول
1
الأول
1
2
الثاني
3
3
الثالث
6
4
الرابع
10
5
الخامس
15
6
الساس
21
7
الثالث (3) و الرابع (4) والخامس (5)
كيف نصل الى 10 ( الحد الرابع ) من 4 و 5 ؟
طبق ما توصلت اليه على
الرابع 10 و الخامس 15
كيف نصل الى 15 من 5 و6 ؟
1 3 6 10 15 21 .....
نحاول ايجاد طريقة نعرف بها معرفة قيمة حد معين من خلال رقم الحد والحد الذي يليه
بعد اختبار المحاولات نجد أن العشرة =( 4 في 5 ) قسمة 2
قيمة الحد = ( رتبة الحد ضرب الحد الذي يليه ) قسمة 2
من الجدول السابق نلاحظ أن
5
الخامس
15
الخامس=خمسة في 6 = 30 قسمة 2= 15
4 استراتيجية البدء من النهاية (Work Backward)
الفكرة:نبدأ من النتيجة النهائية ونعمل عكسيًا حتى نصل إلى البداية.
لدى محمد مبلغ من المال صرف نصفه ثم صرف ثلث الباقي فأصبح لديه 20ريالا فكم كان معه بداية ؟
نبدأ بالعكس : آخر مرة صرف ثلث المبلغ الأخير وبقي 20 ريال هذا الباقي (20) يمثل ثلثي المبلغ السابق وعليه الثلث = 10
يعني أن كامل المبلغ = 30
وعليه يكون المبلغ السابق 30 ريال وهذا يمثل نصف ما كان عنده بداية .
المبلغ في البداية كان 60 ريال .
التأكد :
كان عنده 60ريال صرف نصفها اصبح معه 30 ريال .
كان عنده 30ريال صرف ثلها أي صرف 10
اذا الباقي ثلثين وهو يعادل ما بقي معه 20
وبالتالي الحل صحيح
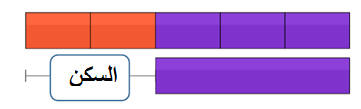
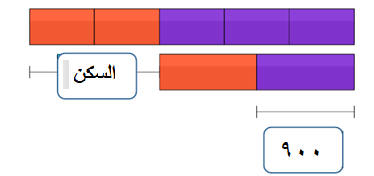
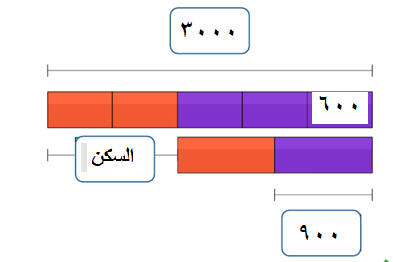
الحل باستخدام الرسم
يصرف محمد خمسي راتبه على المسكن و نصف الباقي من الراتب يصرفه على المعيشة ويبقى معه 900 ريال .
فكم راتبه.؟
الراتب
خمسي الراتب على السكن
الباقي
استراتيجية الرسم والتمثيل البصري (Draw a Diagram)
5
الفكرة:رسم شكل أو مخطط يساعد على فهم المعطيات والعلاقات.
نصف ما محمد يساوي ثلاثة أرباع ما مع صالح . فاذا كان مجموع ما معهما 150 ريال .
فكم كان مع كل منهما ؟
نحسب النسبة بينهما نصف الى 3 أرباع
نصف على ثلاثة أرباع = أربعة على ستة
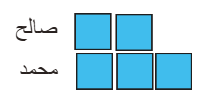
محمد+ صالح= عشر مربعات =150 ريال
كل مربع =15 ريال
محمد 90 ريال
صالح 60 ريال
لدى محمد ثلثي ما لدى صالح فاذ كان مجموع ما معهما معا 160 ريال فكم كان مع كل منهما ؟
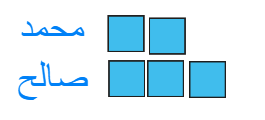

لدى محمد نصف ما مع صالح .اذا أعطى صالح 27 ريال لمحمد يصبح مع كل منهما المبلغ نفسه .
فكم مع كل منهما ؟
بداية ما مع محمد = نصف ما مع صالح
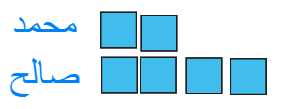
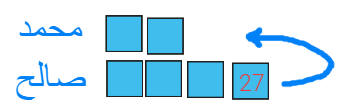
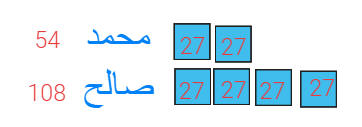
بعد اعطاء صالح 27 ريال لمحمد صال مع كل منهما المبلغ نفسه
6
الفكرة:
نحوّل المسألة إلى معادلة رياضية ونحلها.
شركة نقل لديها حافلات من نوعين. النوع الأول حمولة 40 راكب. والنوع الثاني حمولة 45 راكب .
اذا نقلت الشركة 505 أشخاص في 12 حافلة من النوعين . فكم حافلة من كل نوع؟
يمكن الحل:
- التخمين والتحقق
- بناء جدول
الحل بنظم المعادلات ( معادلتين في مجهولين )
نفرض أن :
عدد حافلات من النوع الأول x
عدد حافلات من النوع الثاني y
x+y=12
40x+45y=505
نكمل الحل
أو بمجهول واحد
النوع الأول x
النوع الثاني 12 ناقص X
نكمل الحل
حل ابداعي بدون معادلات لطالب ابتدائي
نجرب الحافلات الأقل حمولة
12 حافلة بالحمولة الأقل = 480 شخص
المطلوب 505
الفرق 505-480= 25
الفرق بين حمولة الحافلتين = 45
-40= خمسةالفرق بين الحمولةالمطلوبة والحمولة الأقل هو 20
عدد الحافلات الكبيرة = ( فرق بين حمولة الركاب) قسمة (الفرق بين حمولة الباصين )
عدد الحافلات الكبيرة= 5
عدد الحافلات الصغيرة = 7
التأكد 5 في 45 =225
7 في 40= 280
عدد االحافلات 12
الحمولة 505
ويمكن الحل بطريقة الجدول
مجموع ما مع محمد وصالح 500 ريال . فاذا كان ثلثا ما مع صالح
و ثلاثة أرباع ما مع محمد 340 ريال . فكم مع كل منهما ؟
المعادلة الأولى
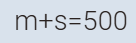 #
#
المعادلة الثانية ثلثي محمد + ثلاثة أرباع صالح = 340
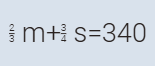 # 2
# 2
بطرح #2 من #1
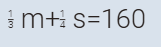 #3
#3
بضرب #3 في اثنين لوجود ثلثين في المعادلة #2
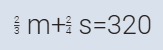 # 4
# 4
بطرح # 4 من #2
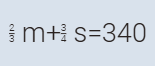 # 2
# 2
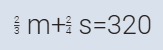 # 4
# 4
ينتج

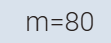
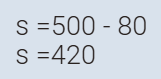
محمد = 80 ثلثا محمد
ثلثا ما مع صالح =280
و ثلاثة أرباع ما مع محمد = 60 ريال
الحل بالنمذجة
مجموع ما مع محمد وصالح 500 ريال . فاذا كان ثلثا ما مع صالح و ثلاثة أرباع ما مع محمد340 ريال .
فكم ريال مع كل منهما ؟
المعادلة الأولى محمد + صالح = 500
في المسألة :
ثلثا صالح
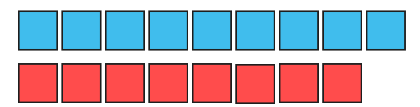
من أجل ذلك نمثل محمد ب ثلاث مربعات بلون
 صالح
صالح
ثلاثة أرباع صالح
من أجل ذلك نمثل صالح بأربع مربعات بلون مختلف
 محمد
محمد
محمد + صالح = 500
+
= 500 ( 1 )
ثلثي صالح + ثلاثة أرباع محمد= 340
+
= 340 ( 2 )
بطرح ( 2 ) من ( 1 ) نحصل على
+
= 160 ( 3 )
لوجود 3 مربعات من كل لون في (1) نضرب المعادلة ثلاثة في 3 فنحصل على
بالتعويض بقيمة ( 3 ) في المعادلة ( 1 ) كالتالي :
( 1 )
= 480 ( 4 )
بطرح المعادلة 4 من المعادلة 1 نحصل على
= 20
= 80
محمد= 80
صالح = 500 ناقص 80= 420
من الممكن حل السؤال باستراتيجية بناء جدول
7استراتيجية
التبسيط (Simplify the Problem)
نحل مسألة مشابهة لكنها أبسط، ثم نعمم الفكرة.
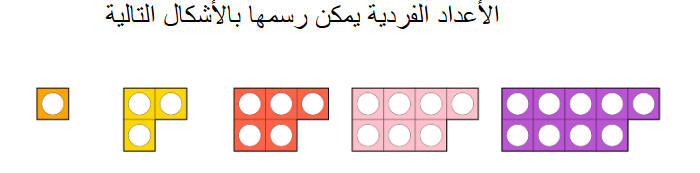
ما مجموع الخمسين عدد فردي الأولى ؟
ما القاعدة التي تحكم هذا النظام ؟
تكمن فكرة التبسيط في البحث عن أعداد فرية أقل من 50 لمعرفة الحل مجموعها
يمكن أن يكون الحل بأكثر من استراتيجية :
استراتيجية بناء جدول
|
المجموع |
الترتيب |
# |
|
1 |
1 |
1 |
|
4 |
3 |
2 |
|
9 |
5 |
3 |
|
16 |
7 |
4 |
|
25 |
9 |
5 |
|
ن تربيع |
ن |
اكتشاف نمط من الجدول كما يمكن حلها باستخدام استراتيجية استخدام نموذج كما في المثال التالي :
استراتيجية استخدام النماذج
|
مساحة |
مجموع |
# |
|
واحد في واحد |
|
1 |
|
اثنين في اثنين |
|
2 |
|
ثلاثة في ثلاثة |
|
3 |
|
أربعة في أربعة |
|
4 |
|
ن في ن |
ن |
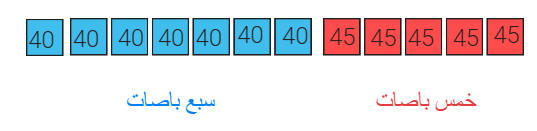
شركة نقل لديها حافلات من نوعين الأول حمولة 40 راكب والثاني حمولة 45 راكب .
اذا نقلت الشركة 505 أشخاص
في 12 حافلة فكم حافلة من كل نوع؟
الفكرة:
المطلوب 505 راكب في 12 باص من نوعين .
النوع الأول حمولة 40 راكب
النوع الثاني حمولة 45 راكب
نفرض أن 12 باص كلهم من الحمولة الأقل فيكون عدد الركاب 480 راكب
معنى ذلك يجب استبدال عدد من الباصات الأقل حمولة بباصات أكثر حمولة
استبدال باص واحد يزيد عدد الركاب بخمسة
الفرق بين 505 و 480 خمسة وعشرين
معنى ذلك نحتاج استبدال خمس باصات

12 باص
9استراتيجية التجربة المنظمة (Systematic Listing)
نكتب جميع الاحتمالات الممكنة بطريقة منظمة دون تكرار.
تقابل 5 أشخاص في مطعم فاذا صافح كل منهم الآخر
فكم عدد المصافحات التي تمت ؟

الأول والثاني الأول والثالث الأول والرابع الأول والخامس
(1,2) , (1,3) , (1,4) ,(1,5)
(2,3) , (2,4) (2,5)
(3,4) ,(3,5)
(4,5)
|
الخامس |
الرابع |
الثالث |
الثاني |
الأول |
|
|
|
|
|
|
|
4 |
3 |
2 |
1 |
|
|
7 |
6 |
5 |
|
|
|
9 |
8 |
|
||
|
10 |
|
|
1 |
2 |
3 |
4 |
المصافحات |
|
|
|
|
|
عدد الأشخاص = 5
عدد المصافحات = 10
ما القاعدة العامة اذا كان العدد ن ؟
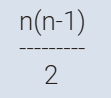
يوجد العديد من المشكلات الرياضية التي يمكن حلها بأكثر من استراتيجة
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع مامعهما معا يساوي 120 ريال
فكم ريال ع كل منهما ؟
ما الاستراتيجيات الممكنة ؟
الاستراتيجيات الممكنة:
1- التخمين والتحقق
2- تبسيط المسألة بجعل النسبة بينهما النصف أو الثلث
3- كتابة معادلة
4- التمثيل بالرسم
5- التمثيل بالنماذج ( مربعات أو مكعبات )
استراتيجية كتابة معادلة :
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع مامعهما معا يساوي 120 ريال فكم مع كل
منهما ؟
ما مع محمد = m
ما مع صالح = s
#1
بالضرب في اثنين
2#
#3
بضرب الطرفين في الوسطين والتبسيط نحصل على
# 4
نعوض من #4 في #2
m=72
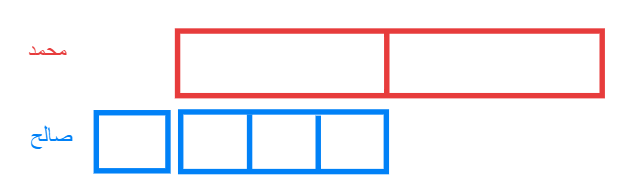
استراتيجية التمثيل بالرسم:
نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح ومجموع مامعهما معا يساوي 120 ريال فكم مع كل
منهما ؟

نصف ما مع محمد يساوي ثلاثة أرباع ما مع صالح
نقسم نصف ما مع صالح الى 3 أجزاء ليتساوى مع ثلاثة أرباع ما مع صالح
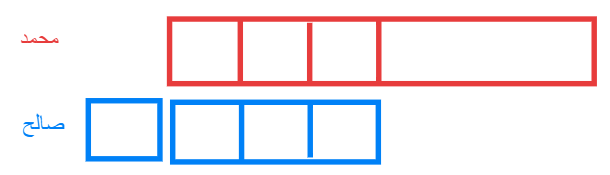
عدد المربعات 10 تساوي 120 ريال كل مربع =12 ريال
ما مع صالح = 48 ريال
ما مع محمد 72 ريال
استراتيجية التمثيل بالنماذج ( مربعات أو مكعبات )
أولا: حساب النسبة بين ما مع محمد الى ما مع صالح
ثانيا :
نستخدم مكعبات او مربعات لتمثيل ما مع كل منهما وفق النسبة
خمس مربعات =120
المربع الواحد =24
محمد = 72
صالح = 48
التأكد نصف ما مع محمد =36
ثلاثة أرباع ما مع صالح = 36