Trapzoid
شبه المنحرف
الفئة المستهدفة
طلاب الصف الأول متوسط الفصل الدراسي الثاني.
الهدف العام
أن يصل الطالب إلى مساحة شبه المنحرف.
المادة العلمية
مساحة شبه المنحرف تساوي نصف حاصل ضرب مجموع قاعدتيه في ارتفاعه.
A=
![]()
واجهة البرمجية
عند النقر على رابط البرمجية تظهر البرمجية التالية:
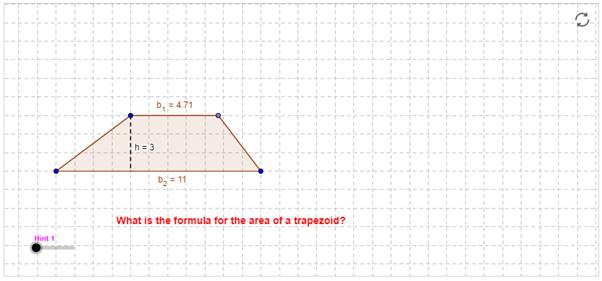
هذه البرمجية أداة بصرية تم تصميمها لمساعدتك للتوصل لمساحة شبه المنحرف.
للتفاعل مع البرمجية...
يمكن للمعلم إتاحة الفرصة للطالب لاستكشاف البرمجية ذاتها.
انقر فوق أي من الدوائر الزرقاء. ماذا تلاحظ؟
انقر فوق أي من الدوائر الزرقاء الموجودة المحددة لأضلاع شبه المنحرف لتغيير أطوالها واتجاهاتها وتغيير ارتفاعها، كما هو موضح بالشكل التالي:
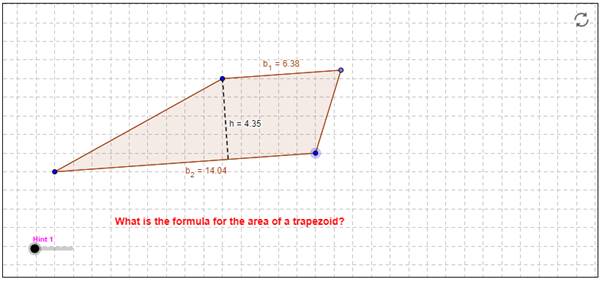
قم بالنقر على
![]()
لاستعادة الشكل الأصلي.
لنبدأ الآن..
ماهي الصيغة الرياضية للتعبير عن مساحة شبه المنحرف؟
باعتبار (H) ارتفاع شبه المنحرف، (b1) طول القاعدة الأولى لشبه المنحرف، (b2) طول القاعدة الثانية لشبه المنحرف.
قم بتحريك النقطة السوداء على شريط التمرير للتلميح ((Hint 1 الموجودة بأسفل البرمجية إلى اليسار.
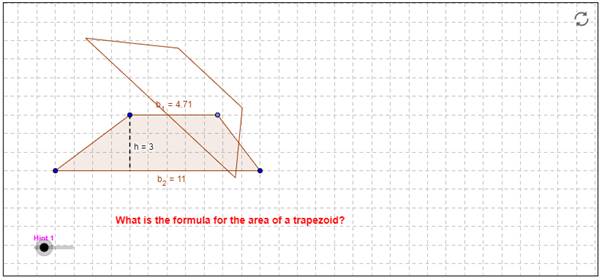
استمر بتحريك النقطة السوداء على شريط التمرير حتى نهاية شريط التمرير.
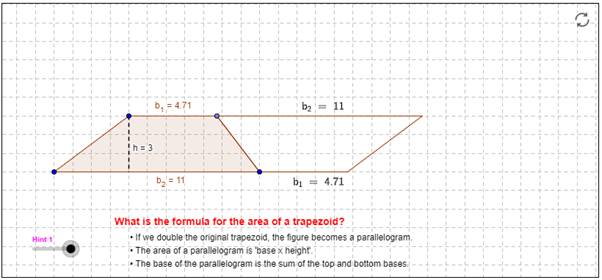
ماهي الصيغة الرياضية للتعبير عن مساحة شبه المنحرف؟
- إذا ضاعفنا شبه المنحرف الأصلي بالطريقة الموضحة بالبرمجية، ماذا ستلاحظ على الشكل الجديد؟
- الشكل سيصبح متوازي أضلاع.
- أحسنت.
- ماهي مساحة متوازي الأضلاع؟
- أحسنت.
- ما علاقة قاعدة متوازي الأضلاع المتكونة بقاعدتي شبه المنحرف؟
- قاعدة متوازي الأضلاع= مجموع قاعدتي شبه المنحرف
- أحسنت.
- عبر عن مساحة متوازي الأضلاع بدلالة طولي قاعدتي شبه المنحرف.
- الارتفاع × مجموع قاعدتي شبه المنحرف
- إذن ماهي مساحة شبه المنحرف الأصلي؟
- هي نصف مساحة متوازي الأضلاع الجديد.
- عبر عنها رياضيًا.
- مساحة شبه المنحرف:
A=
![]()
حيث (H) ارتفاع شبه المنحرف، (b1) طول القاعدة الأولى لشبه المنحرف، (b2) طول القاعدة الثانية لشبه المنحرف
يصل الطالب إلى استنتاج أن مساحة شبه المنحرف هي نصف ارتفاعه مضروبًا في مجموع طولي قاعدتيه. ويعبر عنها رياضيا كما يلي:
A=
![]()
آيات علوي الحبشي