( 3 – 5 ) التحليل بالتجميع المناسب
محتويات التعلم :
المهارات :
تحليل كثيرة الحدود إلى عواملها الأولية بطريقة التجميع المناسب .
الزمن اللازم للتدريس :
حصة واحدة .
الأهداف :
1- أن يحلل الطالب كثيرة حدود إلى عواملها الأولية بطريقة التجميع المناسب .
الوسائل التعليمية :
القطع الجبرية – الكتاب المدرسي – السبورة – جهاز عرض الشفافايات – ورق العمل الخاصة بالمدرس .
التهيئة :
سبق وأن تعرف الطلاب في الدروس الماضية على بعض طرق التحليل لكثيرات الحدود وفي هذا الدرس يتم بإذن الله التعرف على طريقة ثالثة للتحليل .
العرض :
يكتب المعلم على لوح السبورة كثيرة الحدود التالية :
س3 + 2 س2 _ 3 س _ 6
وبمناقشة الطلاب حول كثيرة الحدود هذه يمكن ملاحظة ما يلي :
1- أنها مكونة من أربعة حدود .
2- لا يوجد عامل مشترك لجميع حدودها .
3- أنها لا تمثل مربعاً كاملاً .
4- أنها لا تمثل فرقاً بين مربعين .
ولتحليلها نعمد إلى طريقة التجميع المناسب بهدف إيجاد عامل مشترك أو إظهار المتطابقات الأساسية بعد تجميع حدودها فيكون بذلك هذا الدرس تطبيق لما سبق
دراسته في التحليل بإيجاد العامل المشترك الأكبر أو بطريقة تمييز المتطابقة والمثال التالي يوضح ذلك .
مثال :
حلل كثيرة الحدود س2 + س + س ص + ص
الحل :
 يمكننا
استخدام القطع الجبرية لتجسيد مفهوم هذا التحليل وذلك بوضع القطع التي تمثل حدودها
هذا المقدار وترتيبها في مستطيل بعداه هما ناتج التحليل كما في الشكل التالي :
يمكننا
استخدام القطع الجبرية لتجسيد مفهوم هذا التحليل وذلك بوضع القطع التي تمثل حدودها
هذا المقدار وترتيبها في مستطيل بعداه هما ناتج التحليل كما في الشكل التالي :
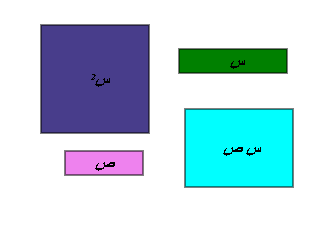
نكون من القطع كلها مستطيل
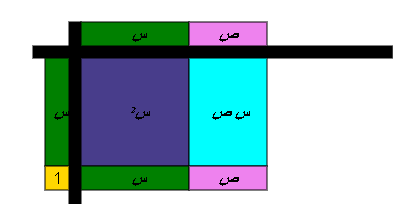
أي أن س2 + س + س ص + ص = ( س + ص ) ( س + 1 ) ، وهو المطلوب .
بعد ذلك يمكن للمعلم أن ينتقل من المحسوس إلى المجرد لإيجاد ناتج هذا التحليل كالتالي :
س2 + س + س ص + ص
= ( س2 + س ) + ( س ص + ص ) [ تجميع مناسب ]
= س ( س + 1 ) + ص ( س + 1 ) [ أخذ العامل المشترك الأكبر ]
= ( س + 1 ) ( س + ص )
وهو المطلوب .
مثال :
حلل كثيرة الحدود س2 + 2 س + 2 ص + س ص باستخدام القطع الجبرية ثم بطريقة التجميع المناسب .
الحل :
يمكننا أن بكون بالقطع الجبرية التي تمثل هذا المقدار مستطيلاً بعداهما ناتج التحليل كما في الشكل التالي :
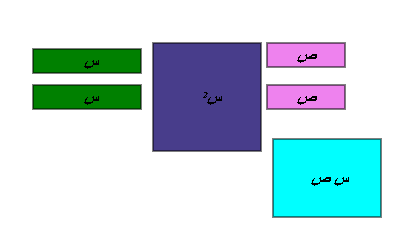
نكون مستطيل
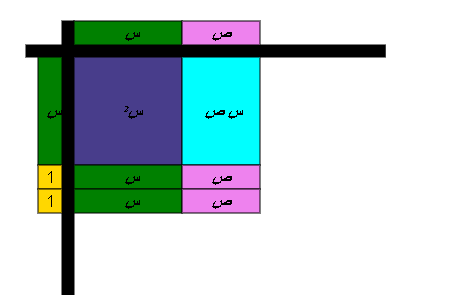
أي أن س2 + 2 س + 2 ص + س ص = ( س + ص ) ( س + 2 )
وهو المطلوب .
أما بطريقة التجميع المناسب فكما يلي :
س2 + 2 س + 2 ص + س ص
= ( س2 + 2 س ) + ( س ص + 2 ص ) [ تجميع مناسب ]
= س ( س + 2 ) + ص ( س + 2 )
= ( س + 2 ) ( س + ص )
وهو المطلوب .
نشاط :
حلل كثيرة الحدود التالية باستخدام القطع الجبرية ثم التجميع المناسب .
2 س ص + ص + 6 س + 3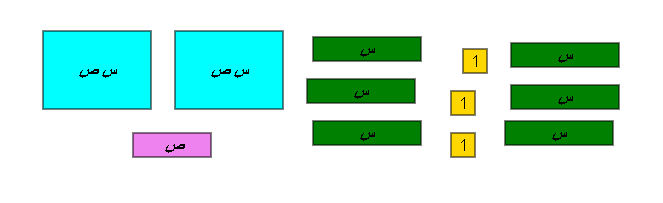
نكون من كل القطع مستطيل
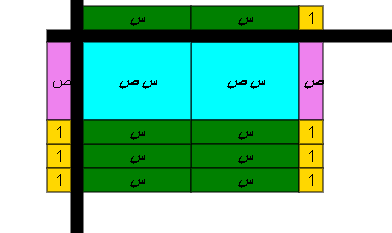
بعدا المستطيل هما نلتج التحليل
( 2 س+1) ( ص+2 )
بعد ذلك يمكن للمعلم ( بعد أن وضَّح للطلاب مفهوم هذا الدرس بطريقة محسوسة ) أن ينتقل إلى حل أمثلة أخرى وبطريقة مجردة كما في الأمثلة التالية :
مثال :
حلل كثيرة الحدود س3 + 2 س2 _ 3 س _ 6
الحل :
نلاحظ أن الحدين س3 ، _ 3 س لهما العامل المشترك س
والحدين 2 س2 ، _ 6 لهما العامل المشترك 2
ثم نتابع عملية التحليل كما يلي :
س3 + 2 س2 _ 3 س _ 6 = ( س3 _ 3 س ) + ( 2 س2 _ 6 )
= س ( س2 _ 3 ) + 2 ( س2 _ 3 )
= ( س2 _ 3 ) ( س + 2 )
وهو المطلوب .
مثال :
حلل كثيرة الحدود أ2 _ 2 أ ب + ب2 – س2
الحل :
نلاحظ أن أ2 _ 2 أ ب + ب2 هي مفكوك لمربع الفرق بين حدين هما أ ، ب لذا نجمِّع الحدود كما يلي ونتابع عملية التحليل :
أ2 _ 2 أ ب + ب2 – س2 = ( أ2 _ 2 أ ب + ب2 ) _ س2
= ( أ _ ب )2 _ س2
= [ ( أ _ ب ) _ س ] [ ( أ _ ب ) + س ]
وهو المطلوب .
نشاط :
حلل كثيرة الحدود التالية : س + ص + أ ص _ أ س
التقويم :
حلل ما يلي بطريقة التجميع المناسب .
أ ) أ س + أ ص _ ب س _ ب ص
ب ) أ2 _ 4 س2 + ب2 + 2 أ ب
الواجب المنزلي :
حلل كثيرة الحدود التالية إلى عوامل بطريقة التجميع المناسب :
4 أ2 + 12 أ + 9 _ أ4