( 3 – 2 ) المتطابقات الأساسية ( 2 )
محتويات التعلم :
المفاهيم :
الفرق بين مربعين – مكعب مجموع حدين – مكعب الفرق بين حدين .
المهارات :
- استخدام معمل الجبر في استنتاج مفكوك ضرب مجموع حدين في الفرق بينهما .
- إيجاد مفكوك ضرب مجموع حدين في الفرق بينهما .
- إيجاد حاصل ضرب عددين باستخدام متطابقة ضرب مجموع حدين في الفرق بينهما .
- استخدام القطع الجبرية في استنتاج مفكوك مكعب مجموع حدين .
- إيجاد مفكوك مكعب مجموع حدين .
- استخدام القطع الجبرية في استنتاج مفكوك مكعب الفرق بين حدين .
- إيجاد مفكوك مكعب الفرق بين حدين .
التعميمات :
- حاصل ضرب مجموع حدين في الفرق بينهما يساوي الفرق بين مربعيهما .
- مكعب مجموع حدين يساوي مكعب الحد الأول زائداً ثلاثة أضعاف مربع الحد الأول في الحد الثاني زائداً ثلاثة أضعاف الحد الأول في مربع الحد الثاني زائداً مكعب الحد الثالث .
- مكعب الفرق بين حدين يساوي مكعب الحد الأول مطروحا منه ثلاثة أضعاف مربع الحد الأول في الحد الثاني زائداً ثلاثة أضعاف الحد الأول في مربع الحد الثاني مطروحا منه مكعب الحد الثالث .
الزمن اللازم للتدريس :
حصتان .
الأهداف :
1- أن يستنتج الطالب مفكوك ضرب مجموع حدين في الفرق بينهما باستخدام القطع الجبرية .
2- أن يوجد الطالب مفكوك ضرب مجموع حدين في الفرق بينهما .
3- أن يوجد الطالب حاصل ضرب عددين باستخدام مفكوك ضرب مجموع حدين في الفرق بينهما .
4- أن يستنتج الطالب مفكوك مكعب مجموع حدين باستخدام القطع الجبرية .
5- أن يوجد الطالب مفكوك مجموع حدين .
6- أن يستنتج الطالب مفكوك مكعب الفرق بين حدين باستخدام القطع الجبرية .
7- أن يوجد الطالب مفكوك مكعب الفرق بين حدين .
الوسائل التعليمية :
القطع الجبرية – البطاقة الجبرية – السبورة – الكتاب المدرسي – جهاز عرض الشفافيات – ورق العمل الخاص بالدرس .
التهيئة :
يناقش المعلم مع الطلاب المتطابقتين الأساسيتين الأولى والثانية عن طريق البطاقة والقطع الجبرية ومن ثم ينطلق إلى المتطابقة الأساسية الثالثة .
العرض :
بعد أن يراجع المعلم مع الطلاب المتطابقتين الأساسيتين الأولى والثانية يتم عرض المتطابقة الأساسية الثالثة كالتالي :
( جـ ) ضرب مجموع حدين في الفرق بينهما
يقوم المعلم بتمثيل المقدار ( س + ص ) ( س _ ص ) كالتالي :
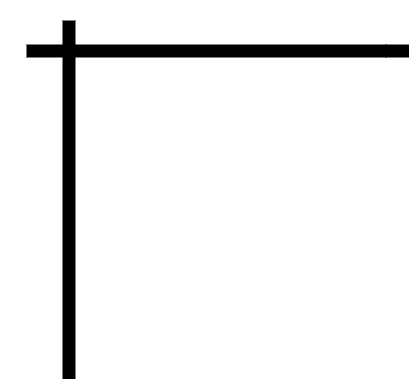
يتم تمثيل الضرب بهذه القطعة حيث يتم تمثيل المقدار الأول على المحور الأفقي
وتمثيل المقدار الثاني على المحور الرأسي
المقدار الأول س +ص
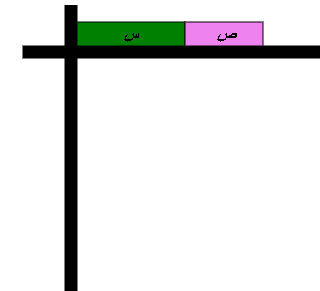
المقدار الثاني
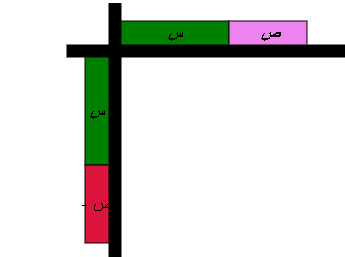
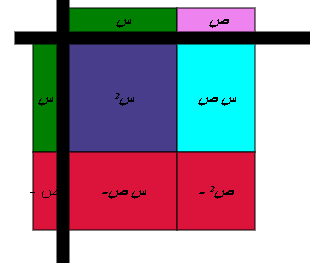
وحيث ان العدد زنظيره = صفر فان
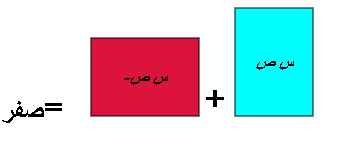
وعليه يكون
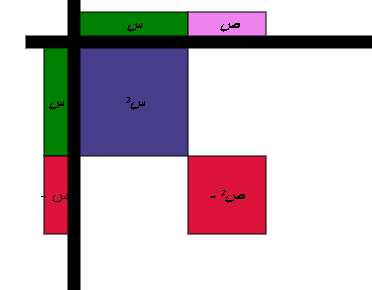

أي أن حاصل ضرب حدين في الفرق بينهما يساوي الفرق بين مربعيهما .
مثال :
أوجد مفكوك ( س + 3 ) ( س _ 3 ) باستخدام البطاقة والقطع الجبرية ؟
الحل :
يمكن تمثيل مفكوك ( س + 3 ) ( س _ 3 ) باستخدام البطاقة والقطع الجبرية كالتالي :
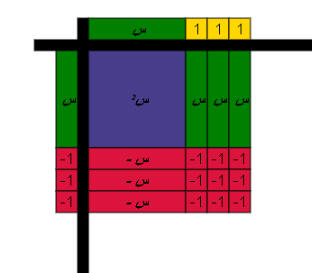
وحيث ان العدد ونظيره = صفر
فان
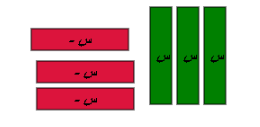
فيكون الناتج
س 2 _ 9
أي أن ( س + 3 ) ( س _ 3 ) = س 2 _ 9
بعد ذلك يمكن للمعلم أن ينتقل بالطلاب من المحسوس إلى المرد لإيجاد مفكوك :
( س + 3 ) ( س _ 3 ) كالتالي :
( س + ص ) ( س _ ص ) = س2 _ ص2
( س + 3 ) ( س _ 3 ) = س2 _ 9
وهو المطلوب .
نشاط :
أوجد مفكوك : ( 2 س + 3 ) ( 2 س _ 3 )
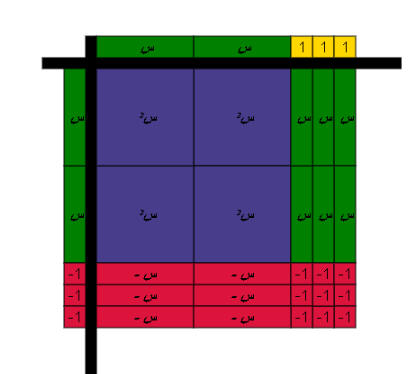
باستبعاد الزوج الصفري يكون الناتج
4 س2 - 9
وهنا يمكن للمعلم أن يوضح للطلاب كيفية الاستفادة من المتطابقة الأساسية الثالثة في إيجاد ناتج ضرب عددين لا يمكن إيجاده من أول وهلة . والمثال التالي يوضح ذلك .
مثال :
استخدم الصيغة ( س + ص ) ( س _ ص ) = س2 _ ص2
لإيجاد ناتج 22 × 18 .
الحل :
تستطيع أن تكتب 22 × 18 كالتالي :
( 20 + 2 ) ( 20 _ 2 ) = 20 2_ 2 2 =400 _ 4 = 396
وهو المطلوب .
نشاط :
استخدم الصيغة ( س + ص ) ( س _ ص ) = س2 _ ص2 لإيجاد ناتج
105 × 95 .
الحل :( د ) مكعب مجموع حدين :
يقوم المعلم هنا باستخدام القطع الجبرية التي تمثل س3 وَ ص3 وملحقاتها لبناء مكعب كبير من هذه القطع كما في الشكل التالي :
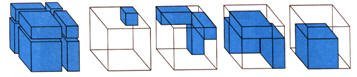
حيث سيلاحظ الطلاب أن هذا المكعب الكبير مكون من المكعب س3 والمكعب ص3 وثلاث قطع تمثل س2 ص ، وثلاث قطع تمثل س ص2 فيستنتج الطالب أن :

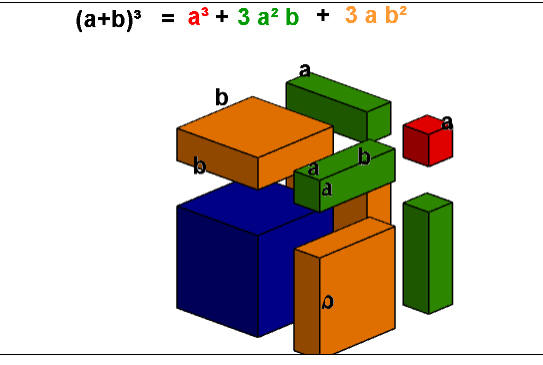
أي أن مكعب مجموع حدين يساوي مكعب الحد الأول زائداً ثلاثة أضعاف مربع الحد الأول في الحد الثاني زائداً ثلاثة أضعاف الحد الأول في مربع الحد الثاني زائداً مكعب الحد الثاني .
البرمجية
https://aghandoura.com/SIGMA/The%20third%20power%20sum.html
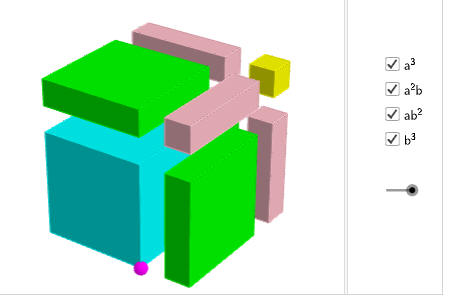
البرمجية 2
https://aghandoura.com/A/mdbrjxhzk-Cube-of-a-Sum.html
مثال :
أوجد مفكوك ( س + 2 )3 باستخدام المتطابقة الرابعة .
الحل :
علماً أن ( س + ص )3 = س3 + س2 ص + 3 س ص2 + ص3
ولذلك فإن (س+2)3 = س3+3 × س2 × 2 + 3 س × 2 2 + 2 3
= س3 + 6 س2 + 12 س + 8
ومما تجدر الإشارة به هنا أنه بالإمكان بناء مكعب باستخدام القطع الجبرية حيث طول ضلع هذا المكعب يمثل ( س + 2 ) .
نشاط :
باستخدام المتطابقة الأساسية الرابعة أوجد مفكوك
(س + 1 )3 .
الحل :
( هـ ) مكعب الفرق بين حدين :
يقوم المعلم باستخدام القطع الجبرية التي تمثل س3 وَ ص3 وملحقاتها ببناء مكعب كبير ، نعتبر أن طول ضلع هذا المكعب الكبير هو س أي أن حجمه س3 والمطلوب هو إيجاد حجم المكعب الذي طول ضلعه هو ( س _ ص ) فسنلاحظ أن حجم هذا المكعب يساوي
حجم المكعب الأساسي س3 مطروحاً منه حجوم القطع المتبقية كما في الشكل التالي :
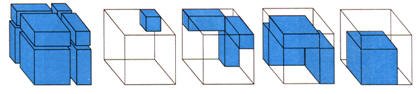
حيث سيلاحظ الطلاب أن :
( س+ص )3 =س3_ 3 ( س_ص )2 ص _ 3 ( س _ ص ) ص2 _ ص3
= س3 _ 3 ص ( س _ ص ) [ ( س _ ص ) + ص ] _ ص3
= س3 _ 3 ص ( س _ ص ) س _ ص3
= س3 _ 3 س ص ( س _ ص ) _ ص3
= س3 _ 3 س2 ص + 3 س ص2 _ ص3
فنستنتج من ذلك أن :
( س _ ص )3 = س3 _ 3 س2 ص + 3 س ص2 _ ص3
أي أن : مكعب الفرق بين حدين يساوي مكعب الحد الأول مطروحاً منه ثلاثة أضعاف مربع الحد الأول في الحد الثاني زائداً ثلاثة أضعاف الحد الأول في مربع الحد الثاني مطروحاً منه مكعب الحد الثاني .
مثال :
أوجد مفكوك ( 2 أ _ 3 )3 باستخدام المتطابقة الأساسية الخامسة ؟
الحل :
علماً أن ( س _ ص )3 = س3 _ 3 س2 ص + 3 س ص2 _ ص3
ولذلك فإن :
(2 أ _ 3)3 = (2 أ)3 _ 3 (2 أ)2 × 3 + 3 (2 أ) × 3 2 _ 3 3
= 8 أ3 _ 36 أ2 + 54 أ _ 27
نشاط :
باستخدام المتطابقة الأساسية الخامسة أوجد مفكوك : ( 2 _ 3 ب )3
الحل :
التقويم :
- باستخدام القطع الجبرية استنتج مفكوك ضرب مجموع حدين في الفرق بينهما ؟
- أوجد مفكوك المقدار التالي : ( أ _ 5 ب ) ( أ + 5 ب )
- باستخدام متطابقة ضرب مجموع حدين في الفرق بينهما أوجد حاصل ما يلي:54×66.
- باستخدام القطع الجبرية استنتج مفكوك مكعب مجموع حدين .
- أوجد مفكوك المقدار التالي : ( 2 أ + 3 ب )3
- باستخدام القطع الجبرية استنتج مفكوك مكعب الفرق بين حدين .
- أوجد مفكوك المقدار التالي : ( 2 أ _ 3 ب )3
الواجب المنزلي :
أوجد مفكوك ما يلي :
( س3 + 1 ) ( س3 _ 1 )
( 1 + 3 ب )3