( 3 - 11 ) حل معادلة الدرجة الثانية في مجهول واحد بطريقة إكمال المربع
البرمجية
https://aghandoura.com/SIGMA/17.html
محتويات التعلم :
المهارات :
- أن يكمل الطالب عبارة رياضية على الصورة : أ س2 + ب س لتصبح مربعاً كاملاً باستخدام القطع الجبرية .
- أن يحل الطالب معادلة الدرجة الثانية في مجهول واحد بطريقة إكمال المربع باستخدام القطع الجبرية .
الزمن اللازم للتدريس :
حصتان
الأهداف :
1- أن يستخدم الطالب القطع الجبرية لإكمال عبارة رياضية على الصورة أ س2 + ب س لتصبح مربعاً كاملاً .
2- أن يستخدم الطالب القطع الجبرية لحل معادلة الدرجة الثانية في مجهول واحد بطريقة إكمال المربع .
الوسائل التعليمية :
القطع الجبرية - البطاقة الجبرية - السبورة - جهاز عرض الشفافيات - ورق العمل الخاص بالدرس .
التهيئة :
يذكر المعلم الطلاب بالصورة العامة لمعادلة الدرجة الثانية في مجهول واحد هي :
أ س2 + ب س + جـ
كما يذكرهم أيضاً بأن المتطابقة الأساسية الأولى وهي :
( س+ ص )2 = س2 + 2 س ص + ص2
العرض :
يكتب المعلم على السبورة الصورة التالية :
أ س2 + ب س
ويطلب من الطلاب ملاحظاتهم على هذه الصورة مقارنة بالصورة العامة لمعادلة الدرجة الثانية في مجهول واحد في طرفها الأيمن والذي هو على الصورة :
أ ب2 + ب س + جـ والمطلوب الآن هو كيف يمكن أن نجعل هذا المقدار المعطى مربعاً كاملاً ، والأمر هنا لا يخلو من حالتين :
الحالة الأولى :
أن يكون المقدار يمثل مربع مجموع حدين على الصورة أ س2 + ب س
الحالة الثانية :
أن يكون المقدار المعطى يمثل مربع الفرق بين حدين على الصورة أ2 س2 _ ب س
الحالة الأولى :
أن يكون المقدار يمثل مربع مجموع حدين على الصورة أ س2 + ب س وفي هذه الحالة نتبع الخطوات التالية :
1- نمثل هذا المقدار بالقطع الجبرية المناسبة في الربع الأول من البطاقة .
2- نقوم ببناء مربع في هذا الربع بإضافة القطع الجبرية المناسبة والتي تمثل الحد ( جـ ) .
3- نضع في المجرى الأفقي والرأسي القطع الجبرية المناسبة وبالضرورة تكون متماثلة وهو ما يمثل مربع مجموع حدين .
والمثال التالي يوضح ذلك .
مثال :
أكمل العبارة س2 + 6 س لتصبح مربعاً كاملاً باستخدام البطاقة والقطع الجبرية ؟
الحل :
نتبع الخطوات التالية :
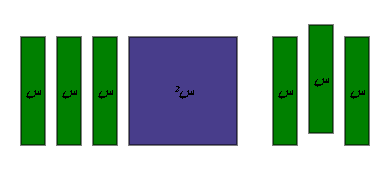
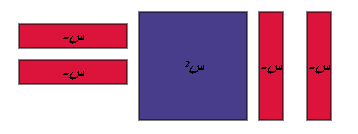
1- نمثل المقدار
2 - نقوم ببناء مربع بإضافة القطع الجبرية المناسبة ومقدار الإضافة
يمثل الحد
( جـ ) كما في الشكل التالي :
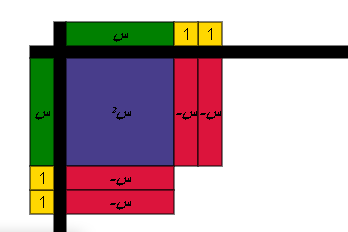
3- نضع في المجرى الأفقي والرأسي القطع الجبرية المناسبة والتي تكون بالضرورة متماثلة وهي ما تمثل مربع مجموع حدين كما في الشكل التالي :
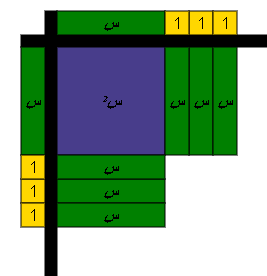= صفر
نضيف 9 للطرفين لاكمال المربع
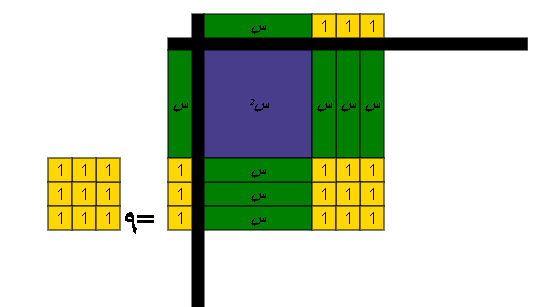
أي أن ( س + 3 )2 = س2 + 6 س + 9 فيكون المقدار المضاف على العبارة (س2 + 6 س) لكي تصبح مربعاً كاملاً هو 9 .
س+3=3 ومنها س=صفر
س+3=-3 ومنها س=-6
نشاط :
أكمل العبارة : س2 + 4 س لتصبح مربعاً كاملاً باستخدام البطاقة والقطع الجبرية .
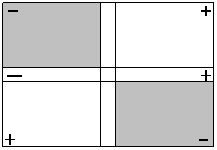الحل
:
=
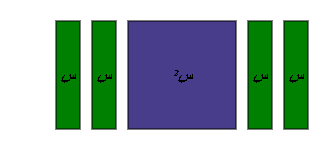
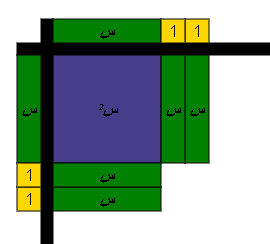صفر
نكمل المربع باضافة 4 الى الطرفين
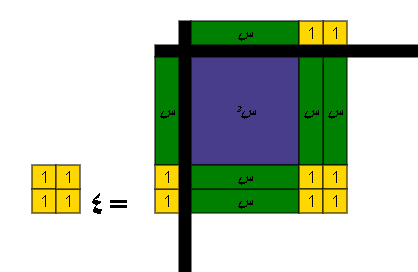
س+2=2 ومنها س=صفر
س+2= -2 ومنها س= 4
الحالة الثانية :
أن يكون المقدار المعطى يمثل مربع الفرق بين حدين على الصورة :
أ2 س2 _ ب س وفي هذه الحالة نتبع الخطوات التالية :
1- نمثل الحد الأول بالقطع الجبرية المناسبة في الربع الأول للبطاقة الجبرية .
2- نمثل الحد الثاني بالقطع الجبرية المناسبة موزعة بالتساوي بين الربعين الثاني والرابع للبطاقة .
3- نبني مربعاً بإضافة المقدار الصفري بالقطع الجبرية المناسبة في الربع الثالث ، وتكون هذه القطع تمثل الحد ( جـ ) [ وذلك باعتبار عدم وجود المجرى الأفقي والرأسي للبطاقة ] .
4- نقوم بوضع القطع الجبرية المناسبة في المجريين الأفقي والرأسي وحاصل ضربهما يمثل مربع الفرق بين الحدين .
والمثال التالي يوضح ذلك .
مثال :
أكمل العبارة س2 _ 6 س لتصبح مربعاً كاملاً باستخدام البطاقة والقطع الجبرية ؟
الحل :
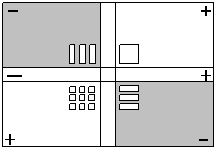
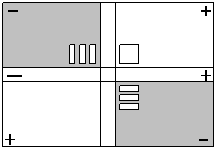بتنفيذ الخطوات المشار إليها يكون لدينا الأشكال التالية :
=
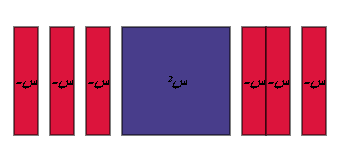
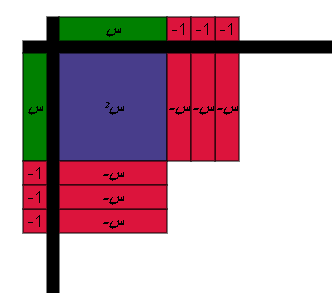صفر
نضيق 9 لاكمال المربع
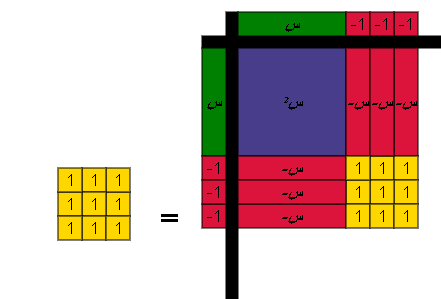
أي أن ( س _ 3 )2 = س2 _ 6 س + 9 فيكون المقدار المضاف على العبارة (س2_6 س) لتصبح مربعاً كاملاً = 9 .
س _ 3 = 3
س = 6
س _ 3 = -3
س=صفر
نشاط :
أكمل العبارة س2 _ 4 س لتصبح مربعاً كاملا
مما سبق يتضح أننا لكي نكمل عبارة لتصبح مربعاً كاملاً نضيف إليها مربع نصف معامل س .
بعد ذلك ينتقل المعلم إلى شرح حل معادلات الدرجة الثانية في مجهول واحد بطريقة إكمال المربع والذي لا يخلو من حالتين أيضاً .
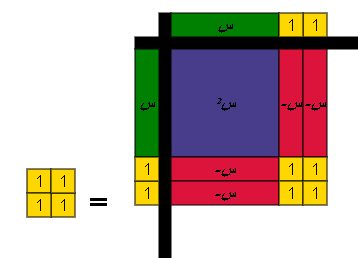
= صفر
اكمال المربع
التقويم :
1- أكمل العبارة س2 _ 2 س لتصبح مربعاً كاملاً ؟
2- حل المعادلة س2 _ 4 س _ 5 = 0 بطريقة إكمال المربع ؟
الواجب المنزلي :
حل المعادلة س2 + 4 س + 12 = 0 بطريقة إكمال المربع ؟