محتويات التعلم :
المفاهيم :
معادلة الدرجة الثانية .
المهارات :
- تمييز معادلة الدرجة الثانية في مجهول واحد من غيرها من المعادلات.
- استخدام القطع الجبرية لحل معادلة الدرجة الثانية في مجهول واحد بطريقة التحليل .
التعميمات :
- كل معادلة تحتوي بعد تبسيطها على مجهول واحد أعلى درجة له فيها هي الدرجة الثانية تسمى معادلة من الدرجة الثانية ذات مجهول واحد .
- الصورة العامة لمعادلة الدرجة الثانية في مجهول واحد هي : أ س2 + ب س + جـ
الزمن اللازم للتدريس :
حصتان .
الأهداف :
1- أن يذكر الطالب معنى معادلة من الدرجة الثانية في مجهول واحد .
2- أن يميِّز الطالب معادلة الدرجة الثانية في مجهول واحد عن غيرها من المعادلات .
3- أن يحل الطالب معادلة الدرجة الثانية في مجهول واحد بطريقة التحليل باستخدام القطع الجبرية.
الوسائل التعليمية :
القطع الجبرية – البطاقة الجبرية – السبورة – جهاز عرض الشفافيات – ورق العمل الخاص بالدرس .
التهيئة :
يراجع المعلم مع الطلاب الفرق بين المتطابقة والمعادلة كما سبق إذ عرفت المعادلة بأنها مساواة بين عبارتين رياضيتين غير متكافئين ويعطي المعلم أمثلة لصور من المعادلات التي تحقق هذا التعريف .
العرض :
يكتب المعلم على لوح السبورة الصورة التالية :
أ س2 + ب س + جـ .
وبمناقشة الطلاب حول خصائص هذه الصورة سنجد أنها تمثل معادلة .
- المعاملات أ ، ب ، جـ تمثل أعداد .
- المجهول فيها واحد هو س .
- أكبر أس مرفوع له المجهول س هو 2 أي أن هذه المعادلة ذات مجهول واحد من الدرجة الثانية .
وبمناقشة المعلم أيضاً للطلاب في عقد مقارنة بين الطرف الأيمن لهذه الصورة مع درس سابق سنجد أن الطرف الأيمن يمثل ثلاثي حدود مما سيسهل على الطلاب فهم هذا الدرس كما سيأتي .
الطرف الأيمن من معادلة الدرجة الثانية في مجهول واحد صورته لا يخلو من أربع حالات ولكل حالة طريقتها الخاصة في الحل وقد سبق تفصيل ذلك في درس تحليل ثلاثي الحدود وفي الأمثلة
التالية مزيد توضيح لذلك .
مثال :
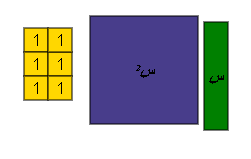
حل المعادلة س2 + 5 س + 6 = 0 باستخدام البطاقة والقطع الجبرية .
الحل :
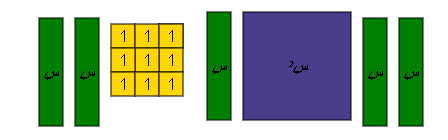
أي أن س2 + 5 س + 6 = 0
![]() ( س + 3 ) ( س + 2 ) = 0
( س + 3 ) ( س + 2 ) = 0
![]() فإما
س + 3 = 0 س = _ 3
فإما
س + 3 = 0 س = _ 3
![]() أو
س + 2 = 0 س = _ 2
أو
س + 2 = 0 س = _ 2
إذاً ح = } _3 ، _ 2 {
وهو المطلوب
نشاط :
حل المعادلة : س2 + 2 س + 1 = 0
مثال :
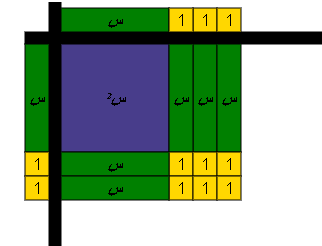
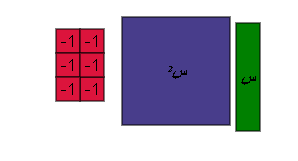
حل المعادلة س2 _ 4 س + 4 = 0 باستخدام البطاقة والقطع الجبرية ؟
الحل :
نقوم بتحليل الطرف الأيمن ثم مساواته بالصفر لإيجاد الحل كما في الأشكال والخطوات التالية:
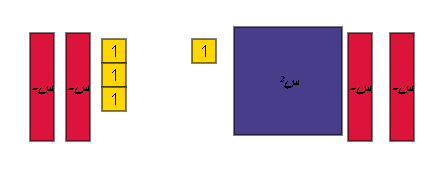
أي أن س2 _ 4 س + 4 = 0
![]() ( س _ 2 ) ( س _ 2 ) = 0
( س _ 2 ) ( س _ 2 ) = 0
![]() فإما
س _ 2 = 0 س = + 2
فإما
س _ 2 = 0 س = + 2
![]() أو
س _ 2 = 0 س = + 2
أو
س _ 2 = 0 س = + 2
إذاً ح = } + 2 {
وهو المطلوب
نشاط :
حل المعادلة س2 _ 2 س + 1 = 0
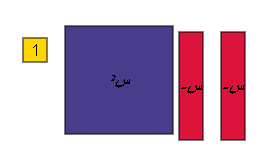
مثال :
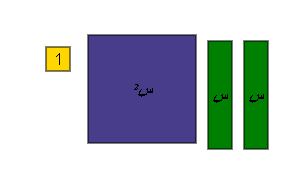
حل المعادلة س2 + س _ 6 = 0 .
الحل :
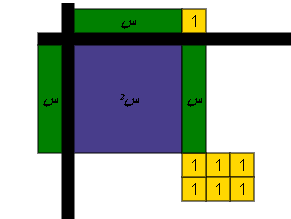
نضيف أزواج صفرية
أي أن س2 + س _ 6 = 0
![]() ( س + 3 ) ( س _ 2 ) = 0
( س + 3 ) ( س _ 2 ) = 0
![]() فإما س + 3 = 0 س = _ 3
فإما س + 3 = 0 س = _ 3
![]() أو س _ 2 = 0 س = + 2
أو س _ 2 = 0 س = + 2
إذا ح = } _ 3 ، + 2 {
وهو المطلوب
نشاط :
حل المعادلة س2 + س _ 6 = 0
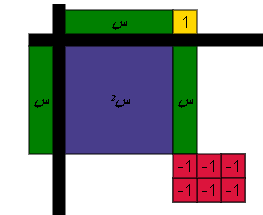
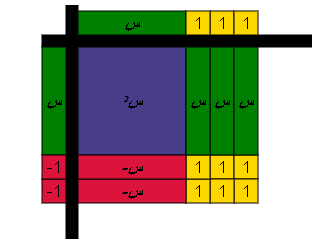
نضيف أزواج صفرية
س+3=صفر
س-2 صفر
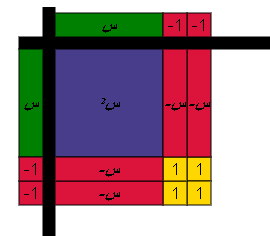
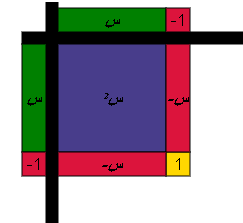
مثال :
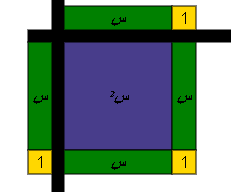
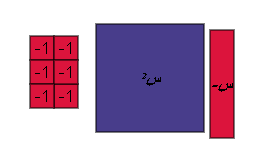
حل المعادلة س2 _ س _ 6 = 0
الحل :
نقوم بتحليل الطرف الأيمن ثم مساواته بالصفر كالتالي :
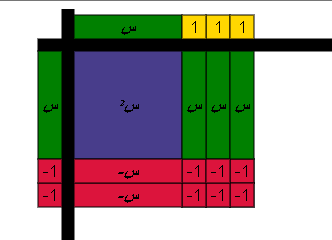
نكمل الشكل باضافة أزواج صفرية
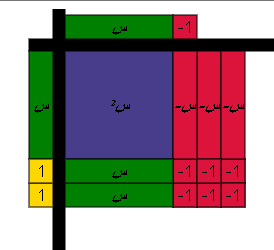
أي أن : س2 _ 6 س _ 6 = 0
![]() ( س _ 3 ) ( س + 2 ) = 0
( س _ 3 ) ( س + 2 ) = 0
![]() فإما س _ 3 = 0 س = + 3
فإما س _ 3 = 0 س = + 3
![]() أو س + 2 = 0 س = _ 2
أو س + 2 = 0 س = _ 2
إذاً ح = } + 3 ، _ 2 {
وهو المطلوب
نشاط :
حل المعادلة س2 _ س _ 2 = 0
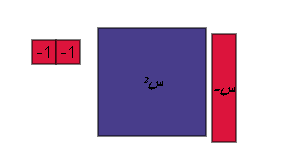
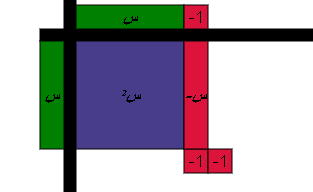
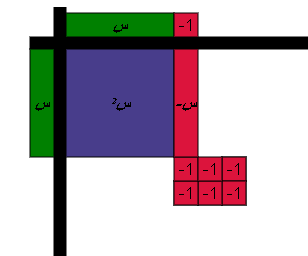
اضافة زوج صفري
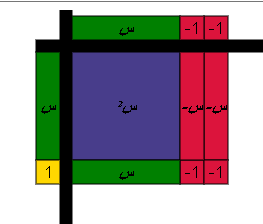
س-2=صفر ومنها س= 2
س+1= صفر ومنها س= -1
التقويم :
1- هل المعادلة التالية تمثل معادلة من الدرجة الثانية في مجهول واحد أم لا ، ولماذا .
س2 + 2 ص + 3 = 0
2- حل المعادلة س2 + 7 س + 6 = 0 ؟
الواجب المنزلي :
حل المعادلة س2 _ 7 س + 6 = 0 ؟