( 3 - 1 ) المتطابقات
محتويات التعلم :
المفاهيم :
المتطابقة - المعادلة - مربع مجموع حدين - مربع الفرق بين حدين.
المهارات :
- تمييز المتطابقة من المعادلة .
- استخدام القطع الجبرية في استنتاج مفكوك مربع مجموع حدين .
- إيجاد مفكوك مربع مجموع حدين .
- استخدام القطع الجبرية في استنتاج مفكوك مربع الفرق بين حدين .
- إيجاد مفكوك مربع الفرق بين حدين .
- إيجاد قيمة مربع عدد باستخدام صيغ المتطابقات .
التعميمات :
- كل مساواة بين عبارتين رياضيتين متكافئتين تسمى متطابقة .
- كل مساواة بين عبارتين رياضيتين غير متكافئتين تسمى معادلة .
- مربع مجموع حدين يساوي : مربع الحد الأول مضافاً إليه ضعف حاصل ضربهما مضافاً إليه مربع الحد الثاني .
- مربع الفرق بين حدين يساوي مربع الحد الأول مطروحاً منه ضعف حاصل ضربهما مضافاً إليه مربع الحد الثاني
الزمن اللازم للتدريس :
حصتان .
الأهداف :
1- أن يعرِّف الطالب المتطابقة .
2-أن يعرَّف الطالب المعادلة .
3-أن يميِّز الطالب المتطابقة من المعادلة .
4-أن يستنتج الطالب مفكوك مربع مجموع حدين باستخدام القطع الجبرية .
5-أن يوجد الطالب مفكوك مربع مجموع حدين .
6-أن يستنتج الطالب مفكوك مربع الفرق بين حدين باستخدام القطع الجبرية .
7-أن يوجد الطالب مفكوك مربع الفرق بين حدين .
8-أن يوجد الطالب قيمة مربع عدد باستخدام صيغ المتطابقة .
الوسائل التعليمية :
القطع الجبرية - البطاقة الجبرية - السبورة - الكتاب المدرسي - جهاز عرض الشفافيات - ورق العمل الخاص بالدرس .
التهيئة :
يقوم المعلم بمناقشة الطلاب في خاصية توزيع الضرب على الجمع التي سبق أن دُرست من قبل ثم يعطى المقدار التالي س ( س + 2 ) ليطبق عليه هذه الخاصية ( توزيع الضرب على الجمع )
فيكون الناتج هو س2 + 2س وبالتعويض في العبارتين الرياضيتين بقيم مختلفة لـ س يجد الطالب أنهما متكافئتان ، أي لهما القيمة العددية نفسها مهما كانت قيمة المتغير س .
العرض :
يعرض المعلم القطع الجبرية للطلاب موضحاً مكوناتها ومن ثم أهميتها في دراسة مفاهيم وموضوعات الجبر لاستثارة اهتمام الطلاب وتوظيف هذا الاهتمام في فهم موضوعات وحدة العبارات الجبرية ،
فمثلاً المقدار :
من الممكن استخدام أداة الضرب التالية

س ( س + 2 ) يمكن تمثيله كالتالي :
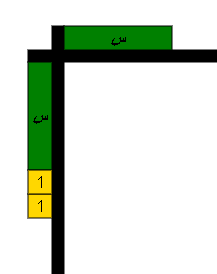
وبعد هذا التمثيل يمكن أن نكمل الجزء المحصور بين هذين المقدارين بالقطع الجبرية الملائمة كالتالي :
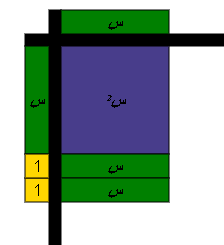
س ( س + 2 ) = س2 + 2 س
ولذلك فإنه من الممكن أن يقال أنه متى استطعنا أن نكمل الجزء المحصور بين المقدارين بالقطع الجبرية الملائمة فإن ذلك يكون لنا متطابقة ، نستنتج أن :

ومن المعلوم لدى الطلاب أن المساواة بين عبارتين رياضيتين غير متكافئتين تسمى معادلة .
مثال :
هل العبارة التالية تمثل متطابقة :
س ( س + 1 ) = س2 + س ؟
الحل :
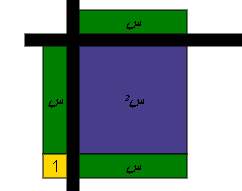
نمثل هذه العبارة الرياضية كالتالي :فنستنتج أن س ( س + 1 ) = س2 + س
أي أن : العبارة المعطاة تمثل متطابقة .
نشاط : ميز فيما يلي المتطابقة من المعادلة باستخدام البطاقة والقطع الجبرية .
أولا:
س ( 3 - س ) = 3 س - س2
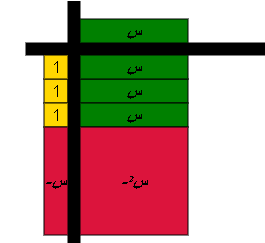
ثانيا
س + 1 = 5 س
- العبارة س ( 3 - س ) = 3 س - س2 تمثل : متطابقة
- العبارة س + 1 = 5 س تمثل : معادلة
وبهذا يستطيع الطالب أن يميز بين المتطابقة والمعادلة إلا أن هناك متطابقات كثيراً ما نستخدمها في إجراء عمليات جبرية متكررة ، أطلق عليها المتطابقات الأساسية ومن ذلك :
( أ ) مربع مجموع حدين :
البرمجية
https://www.aghandoura.com/geogebra/TATBEEK/MOTABBIKAT/1.html
يقوم المعلم بتمثيل المقدار ( س + ص )2 كالتالي :
نستخدم أداة الضرب
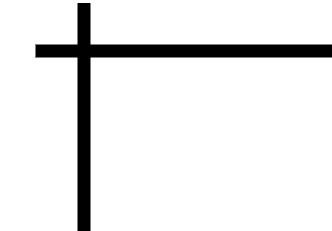
نمثل المقدار الأول على المحور الأفقي
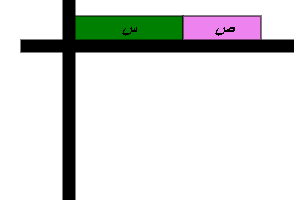
المقدار الثاني على المحور الرأسي
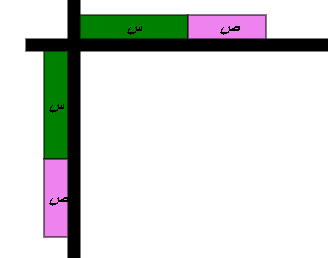
نكمل داخل الحدود
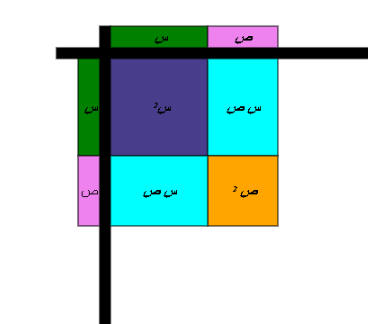
فنستنتج أن :
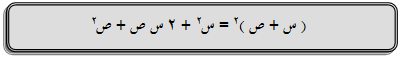
البرمجية
https://aghandoura.com/SIGMA/16.html
أي أن مربع مجموع حدين يساوي مربع الحد الأول زائداً ضعف حاصل ضربهما زائداً مربع الحد الثاني .
مثال :
أوجد مفكوك ( س + 2 )2 باستخدام البطاقة والقطع الجبرية ؟
الحل :
يمكن تمثيل مفكوك ( س + 2 )2 باستخدام البطاقة الجبرية كالتالي :

نمثل المقدار الأول على المحور الأفقي والثاني على المحور الرأسي
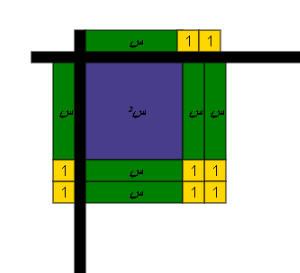
أي أن ( س + 2 )2 = س2 + 4 س + 4
بعد ذلك يمكن للمعلم أن ينتقل بالطلاب من المحسوس إلى المجرد لإيجاد مفكوك مفكوك :
( س + 2 )2 كالتالي :
( س + ص )2 = س2 + 2 س ص + ص2
( س + 2 )2 = س2 + 2 × س × 2 + 2 2
= س2 + 4 س + 4
نشاط :
أوجد مفكوك ( س + 3 )2 ؟
الحل :

نمثل المقدار الأول على المحور الأفقي والثاني على المحور الرأسي
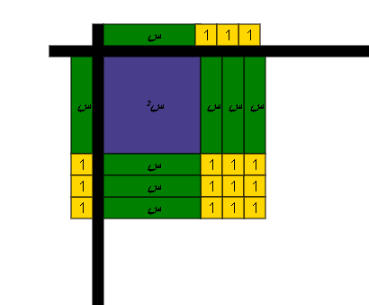
( ب ) مربع الفرق بين حدين :
يقوم المعلم بتمثيل المقدار التالي ( س _ ص )2 كالتالي :

نمثل المقدار الأول على المحور الأفقي والثاني على المحور الرأسي
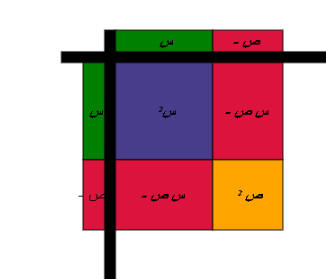

أي أن مربع الفرق بين حدين يساوي مربع الحد الأول مطروحاً منه ضعف حاصل ضربهما مضافاً إليه مربع الحد الثاني .
مثال :
أوجد مفكوك ( س _ 2 )2 باستخدام البطاقة والقطع الجبرية ؟
الحل :
يمكن تمثيل مفكوك ( س _ 2 )2 كالتالي :

نمثل المقدار الأول على المحور الأفقي والثاني على المحور الرأسي
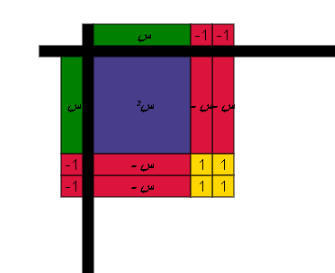
أي أن ( س _ 2 )2 = س2 _ 4 س + 4
بعد ذلك يمكن للمعلم أن ينتقل بالطلاب من المحسوس إلى المجرد لإيجاد مفكوك ( س _ 2 )2
( س _ ص )2 = س2 _ 2 س ص + ص2
( س _ 2 )2 = س2 _ 2 × س × 2 + ( - 2 )2
= س2 _ 4 س ص + 4
نشاط :
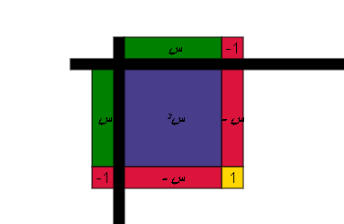
أوجد مفكوك ( س _ 1 )2 ؟
الحل :

نمثل المقدار الأول على المحور الأفقي والثاني على المحور الرأسي
وبعد هذا العرض يمكننا توظيف ما سبق في إجراء حسابات عملية كما في المثال التالي :
مثال :
أوجد قيمة ما يلي باستخدام المتطابقتين الأساسيتين الأولى والثانية :
( أ ) ( 105 )2 ( ب ) ( 19 )2
الحل :
أ ) ( 105 )2 يمكن كتابتها كالتالي :
( 105 )2 = ( 100 + 5 )2
= 100 2 + 2 × 100 × 5 + 5 2
= 10000 + 1000 + 25
= 11025
ب ) ( 19 )2 يمكن كتابتها كالتالي :
( 19 )2 = ( 20 _ 1 )2
= 20 2 _ 2 × 20 × 1 _ 1 2
= 400 – 40 + 1
= 361
نشاط :
باستخدام صيغتي مربع مجموع حدين ومربع الفرق بين حدين أوجد مربعات الأعداد التالية :
( أ ) ( 99 )2 ( ب ) ( 17 )2
الحل :
أ )
ب )
التقويم :
· عرِّف المتطابقة .
· عرِّف المعادلة .
· ميِّز المتطابقة من المعادلة فيما يلي :
س + ص = 4
ص ( س _ 5 ) = ص س – 5 ص
· باستخدام القطع الجبرية استنتج مفكوك مربع مجموع حدين .
· باستخدام القطع الجبرية استنتج مفكوك الفرق بين حدين .
· أوجد مفكوك ما يلي :
( 1 + س )2
( س _ 3 )2
· أوجد قيمة مربع العدد التالي باستخدام المتطابقة الأساسية الأولى :
( 61 )2 .
الواجبات المنزلية :
أوجد مفكوك ما يلي باستخدام جميع المتطابقات :
أ ) ( 2 س + 1 )2 ب ) ( 2 س _ 1 )2