ولو
عرض عليه بهذا الطريقة
ولو
عرض عليه بهذا الطريقة  فيعتقد
أنه معين ، فلابد في البداية توضح هذه الفكرة له ، وحتى نشرح المربع للطالب نعرضه
كالتالي:
فيعتقد
أنه معين ، فلابد في البداية توضح هذه الفكرة له ، وحتى نشرح المربع للطالب نعرضه
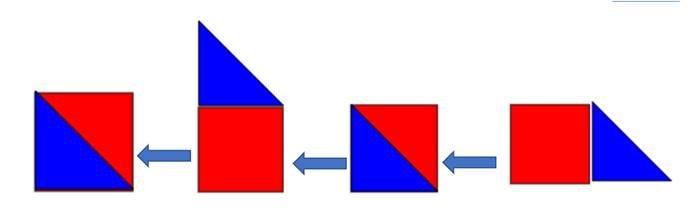
كالتالي:أولاً : نعرض شكل المربع ، ويمكن صنع أكثر من مربع بالنسخ والتكرار كالتالي :
رابعاً :الأشكال الرباعية :
نستطيع باستخدام البرمجية توضيح الأشكال الرباعية وخواصها ، وهي كالتالي :
1-المربع :
لو أردنا شرح مفهوم المكعب للطلاب ، نعرض عليهم المكعب التالي ، ولابد أن يوضح
للطلاب أن المكعب يبقى هو المكعب حتى لو أختلف وضعه لاعتقاد كثير من الطلاب أن
المكعب لابد يكون بوضع واحد  ولو
عرض عليه بهذا الطريقة
ولو
عرض عليه بهذا الطريقة  فيعتقد
أنه معين ، فلابد في البداية توضح هذه الفكرة له ، وحتى نشرح المربع للطالب نعرضه
كالتالي:
فيعتقد
أنه معين ، فلابد في البداية توضح هذه الفكرة له ، وحتى نشرح المربع للطالب نعرضه
كالتالي:
أولاً : نعرض شكل المربع ، ويمكن صنع أكثر من مربع بالنسخ والتكرار كالتالي :
ثانياً : نبدأ بعرض خاصية الأضلاع ونقارن أضلاع كل شكل منها . باستخدام المثلثات كالتالي :
نوضح للطلاب أن الضلع الأول يطابق الثاني يطابق الثالث ، يطابق الرابع باستخدام المثلث الصغير ، فيصل الطالب إلى أن الأضلاع متطابقة ، ثم نقارن الزوايا ، بنفس المثلث ونبين أن الزوايا الأربع قائمة كما في الخطوات الأربع المتتالية :

ومن هذا يعرف الطالب أن الشكل جميع أضلاعه متطابقة ، وجميع زواياه قائمة وهذا هو مفهوم المربع ، ونعمل نفس الخطوة مع المربعات التالية لترسيخ المفهوم .
كما يمكن توضيع خصائص المربع ، وهي أن الأقطار متطابقة ومتقاطعة في المنتصف .
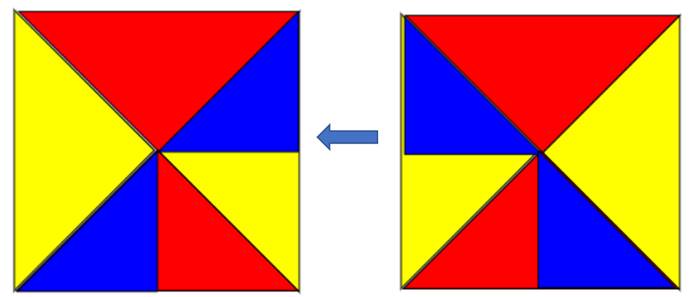
وكذلك أن أقطار المربع متعامدة ، وهذا واضح من المثلثات المستخدمة في الأقطار جميعها قائمة الزاوية .
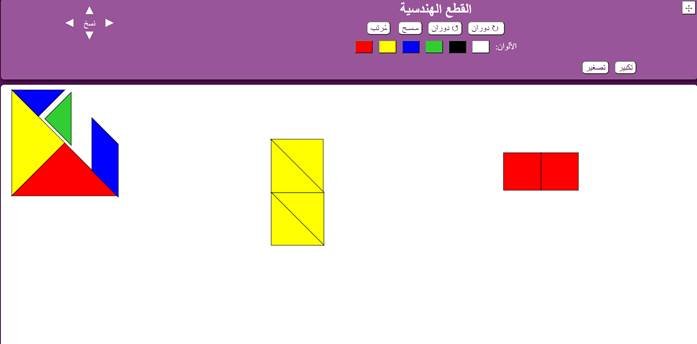
2-المستطيل :
نلاحظ أن القطع لا يوجد فيها مستطيل ، فنكون المستطيل عن طريق جمع مربعين أو أكثر ، ويمكن عمل مستطيل بالمثلثات كذلك ، أو استخدام اشكال أخرى ، كما يلي :
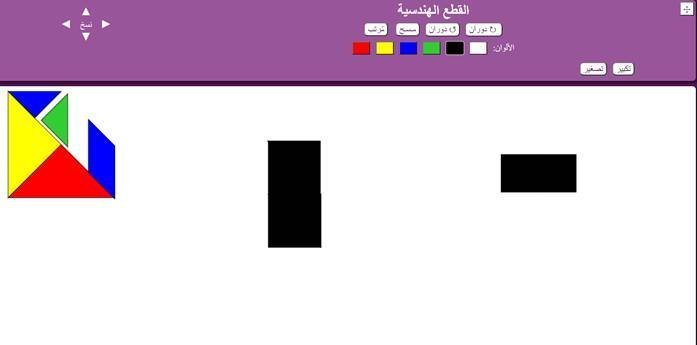
نستطيع تغيير اللون للون الأسود حتى يكون كشكل واحد ، كما يلي :
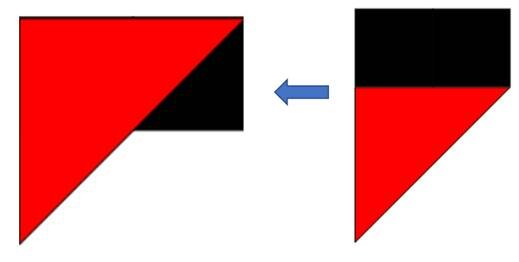
الان نبحث العلاقة بين زوايا المستطيل ، الأول بالتسلسل الاتي :

بعد أستعرض الزوايا يكتشف الطالب أن جميع الزوايا ، قائمة ، وهذا هو مفهوم المستطيل شكل رباعي جميع زواياه قائمة .
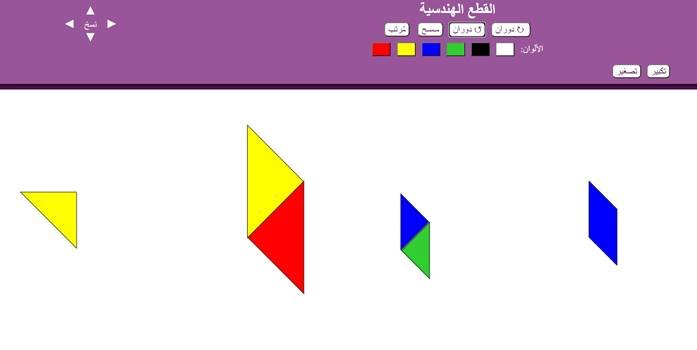
ويمكن توضيع خصائص أضلاعه كما يلي :
فنوضح أن الضلعين المتقابلين متطابقين ، ونفعل نفس الشيء مع الضلعين الأخرين كما يلي:

فنجد أن الضلعين متطابقين ، وبذلك يصل الطالب إلى أن كل ضلعين متقابلين في المستطيل متطابقين .
3-متوازي الأضلاع :
نستطيع باستخدام البرمجية توضيح مفهوم متوازي الأضلاع ، وذلك بعرض متوازي الأضلاع وتوضيح العلاقة بين أضلاعه ، ويمكن استخدام متوازي الأضلاع ، او تكوين متوازيات أضلاع مركبة باستعمال المثلثات كما كما يلي :
في متوازيان الضلعان المركبان نلاحظ أن الأضلاع المتقابلة متطابقة لأنها نفس المثلثات متشابهة ، وهذه زواياهم المتناظرة ، ونستطيع توضيح العلاقة بينهم كذلك ، ولو أردنا أن نوضح العلاقة بين الأضلاع في متوازي الأضلاع الأول كما يلي :
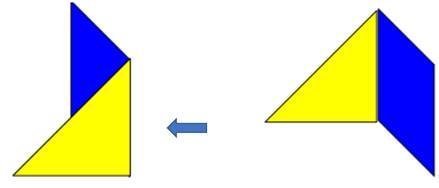
فيلاحظ الطالب أن الضلعين المتقابلين متطابقين ، ونفحص العلاقة بين الضلعين الأخرين ،كما يلي :
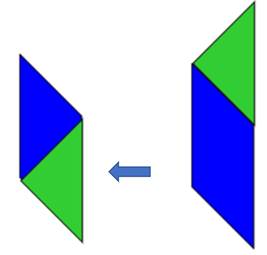
ونلاحظ أن الضلعين المتقابلين متطابقين ، ومن ذلك يستنتج الطالب أن متوازي الأضلاع هو شكل رباعي فيه كل ضلعين متقابلين متطابقين .
ويمكن توضيح العلاقة بين زوايا متوازي الأضلاع ، كما يلي :
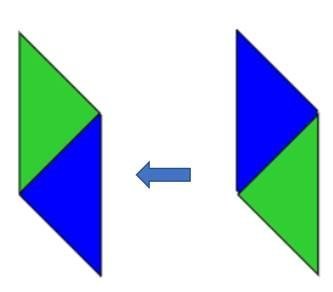
نلاحظ أن الزاويتان المتقابلتان ، باستخدام نفس الزاوية وتدوير المثلث الأخضر ، هما زاويتان متطابقتان ، ونبحث العلاقة بين الزاويتان الأخرى ، كما يلي :
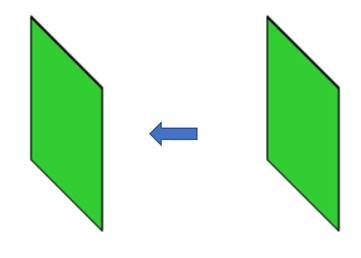
باستخدام متوازي أضلاع أخر نوضع العلاقة بين الزاويتان الأخرى وذلك بتدوير نفس الزاوية حتى تكن على الزاوية الاخرى فنجد انها متطابقة ، وبذلك يصل الطالب إلى خاصية زوايا متوازي الأضلاع ، وهي : أن كل زاويتان في متوازي الأضلاع متقابلتين هما متطابقتين .
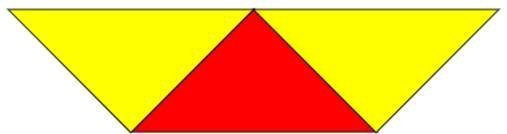
4-شبة المنحرف :
يكن توضيح شبه المنحرف بتكوين أكثر من شكل كما يلي :
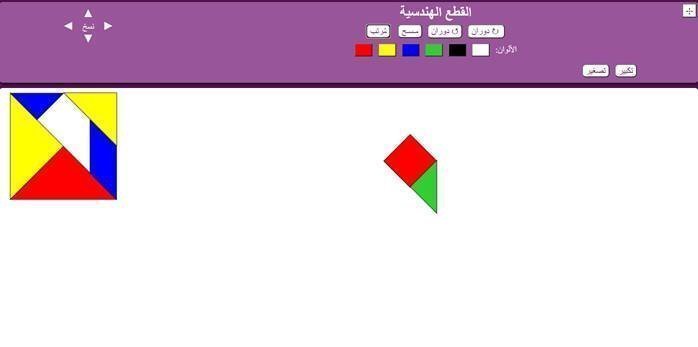
باستخدام المربع والمثلث ، كونا هذا الشكل وهو شبه منحرف ، ونلاحظ فيه أن يتكون من ضلعان متقابلان متوازيان وهذا يتضح من تعامدهم في المربع ، فيكون مفهوم شبة المنحرف هو شكل رباعي في ضلعان متوازيان فقط ، لأنه يتضح أن الضلعان الأخران غير متوازيان ،
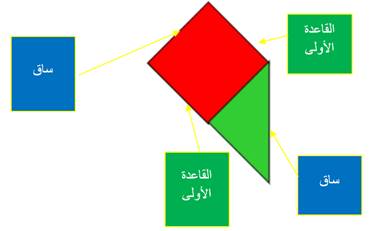
ثم نوضح مسميات هذه الأضلاع ، فالضلعان المتوازيان يسميان قواعد القاعدة الأولى والقاعدة الثانية ، أما الأضلاع الغير متوازية تسمى ساقان,
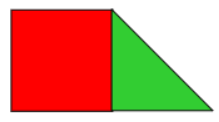
ويسمى متوازي الأضلاع هذا متوازي أضلاع قائم الزاوية . ويمكن عرضه بشكل معتدل كما يلي :
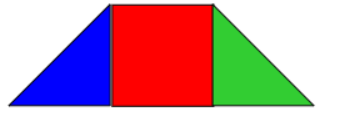
ويمكن توضيح النوع الأخر من شبة المنحرف ، وهو شبة المنحرف متطابق الساقين كما يلي:
ويمكن تمثيلة بطريقة أخرى باستعمال متوازي الأضلاع ومثلث كما يلي :

ويفضل دائماً التنوع في عرض أي شكل حتى يزول اللبس لدى الطلاب ، وتعميق الفهم لديهم .