نظريــة فيثاغــورث

               نظرية فيثاغورس ( العلاقة بين أضلاع المثلث القائم الزاوية )

               نشــاط :

                على الشكل المرسوم في الصفحة التالية مثلث قائم الزاوية نسمى الضلع المقابل للزاوية القائمة ( الوتر ) 0

               وكلا من الضلعين الآخرين تسمى ( ضلع الزاوية القائمة ) 0

             - أطوال ضلعي الزاوية القائمة (  1  ،  1 )

             - طول الوتر  =

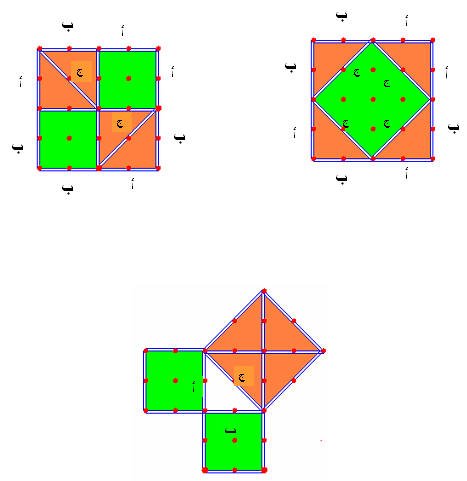
              في الشكل (2 ) رسمنا مربعا على كل ضلع من اضلاع المثلث القائم الزاوية 0

             - ما مساحة المربع المرسوم على كل من ضلعى الزاوية القائمة ؟

             - ما مساحة المربع المرسوم على الوتر ؟

                عند مقارنة المساحة للمربع على الوتر نجد أنها تساوي مجموع     مساحتى المربعين المرسومين على ضلعي الزاوية القائمة وهذا ينطبق على المثلث القائم الزاوية فقط 0

               إذن يمكن صياغة نظرية فيثاغورث على النحو التالي :

                 تابع نظرية فيثاغورث :

                 ويمكن كذلك اثبات نظرية فيثاغورث عن طريق المربع كما هو مرسوم   في الشكل في الصفحة التالية :

                بحيث يكون المربع الداخلي طول ضلعه مساوي للوتر فى المثلث وطول ضلع المربع  أ + ب

              بما أن ( أ + ب )2  = أ2 + 2أب + ب2       

              ومساحة المربع  =  طول الضلع × نفسه 0

                                 = ( أ × ب)(أ × ب )

              والخطوة التالية باعادة ترتيب المربع نجد أن المساحة تمثل :

               (أ + ب ) = أ2 + 2أب  0 مجموع مساحة المربعات الموجودة 0

               وبما أن  أ2 + ب2  = جـ2    المربع الداخلي0

               فيكون  أ2 + ب2 + 2أب =  2أ ب + جـ2

                اذن   أ2  + ب2  = جـ2

                                               نظرية فيثاغورث 0

               ومما سبق يمكننا كذلك توضيح للتلميذات عن الجذور مثلا    2              ففى المثال الأول (1)2 + ( 1)2 = جـ2             نظرية فيثاغورث

                                    2أ = جـ2

                         فيكون جـ =  2       وهو طول الوتر 0

             فاذا كون الشكل الرباعي المربع كما فى الرسم ( شكل 1 ) الذي فيه طول ضلعه 2  2  ،  فيمكن أن تذكر التلميذة ان مساحة المربع  عدد المربعات داخل الشكل ، فنجد أنها تمثل المساحة وتطبيق قانون مساحة المربع طول الضلع × نفسه 0 

                 اذن يكون مساحة المربع = 2   2  × 2   2  = 4 × 2    =8

                 ومن هنا يمكن أن تتعرف التلميذة على معنى   2  ×  2    = 2

              ومن الشكلين (2) و(3) و(4) يمكن التوصل الى معرفة مساحة شبه المنحرف ، وهى تساوى القاعدة الصغرى + القاعدة الكبرى   × الارتفاع

              عن طريق مقارنتها بمساحة المستطيل فى الشكل التالى 0

              حيث أنها تساوي الطول × العرض 0

              وبما ان شبه المنحرف يمثل نصف المستطيل 0

              اذن تكون مساحة شبه المنحرف نصف مساحة المستطيل 0

              حيث ان العرض فى المستطيل يمثل الارتفاع فى شبه المنحرف 0

              والطول يمثل مجموع القاعدتين فى شبه  المنحرف 0

                من هنا نستنتج القانون :

                 وقبل ذلك يتم تعريف التلميذة بان شبه المنحرف شكل رباعي فيه ضلعان متوزيان وأن :

                   1- كل واحد من الضلعين المتوازيين يمثل قاعدة له 0

                   2- كل واحد من الضلعين الغير متوازيين يمثل ساق له ( الارتفاع ) 0