المتطابقــات

المتطابقــات

" المتطابقة هي مساواة بين عبارتين رياضيتين متكافئتين "

باستخدام المكعبات المتداخلة ، تهدف الى توضيح وإيجاد مفكوك المتطابقات بطريقة ملموسة للتلميذات 0

أولا : مربع مجموع حدين : ( س + ص ) 2

س الحد الأول ، ص الحد الثاني ، س + ص مجموع الحدين

حيث س يمثل بثلاث مكعبات ، ومقدار ص بمكعب واحد0

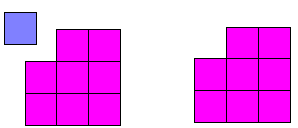
فيكون ( س + ص ) ، يمثل الشكل في الصفحة التالية :

عبارة عن المربع من المكعبات طول ضلعه ( س + ص )

1- توجد مجموع أجزاء الشكل كما هو موضح في الخطوة الثانية 0

2- الأجزاء هى : ( س2 + ص 2 + س ص + س ص )

فيكون ( س + ص )2 = ( س2 + 2س ص + ص2 )

استنتاج :

مربع مجموع حدين = مربع الحد الأول + ضعف الحد الاول × الحد الثاني + ربع الحد الثاني

تطبيــق :

ناقش المتطابــقة التالية ( س + 5 )2

( س + ص ) ² س + ص

س ² + 2 س ص + ص ²

ثانيا : مربع الفرق بين حدين ( س - ص ) 2

لإيجاد مفكوك المتطابقة ( مربع الفرق بين حدين)نقوم بالخطوات التالية : نحدد س الحد الاول ، ص الحد الثاني ، س -ص الفرق بين الحدين0

- نبدأ ببناء مربع من المكعبات طول ضلعه س فيكون مساحته ( س )2

- للحصول على الصبغة ( س - ص ) 2 نقوم بتحديد المقدار ( س - ص

- ( س- ص ) 2 = ( س - ص) (س - ص)

= س( س - ص ) - ص ( س - ص )

= س2 - س ص - س ص + ص2

= س2 -2س ص + ص2

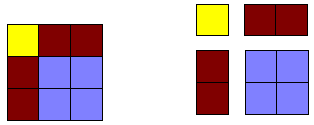
يتضح ذلك من خلال الرسم في الشكل التالى :

1- يمثل اتحاد المربعين مساحتاهما فى : س2 و ص2

2 -يقطع المستطيلين س ص وس ص فيبقي لديناالمربع طول ضلعه ( س- ص )

ومساحته : ( س2 + ص2 ) - (2س ص ) 0

3- وهذا معناه عمليا : ( س - ص )2 = س2 + ص2 -2س ص 0

استنتاج : مربع الفرق بين حدين = مربع الحد الاول - ضعف الحد الاول × الثاني + مربع الحد الثاني 0

تطبـيق : ناقش العبارة (2س - 3 ) 2

س - ص

س ² س ² ص ² 2س ص

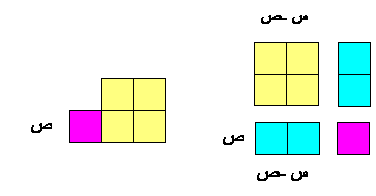
ثالثا : حاصل ضرب مجموع حدين بالفرق بينهما :(الفرق بين مربعين)

توضح س الحد الأول ، ص الحد الثاني0

أي تحليل المتطابق ( س + ص) ( س - ص)

( س + ص ) (س - ص ) = س ( س- ص ) + ص ( س- ص )

= س2 - س ص + س ص - ص2

= س2 - ص2

لإيجاد المفكوك عمليا امام التلميذات نقوم بالتالي :

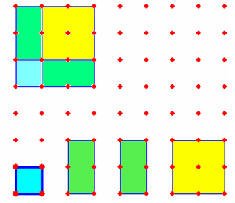
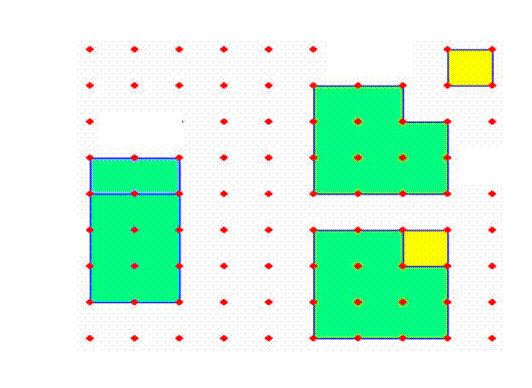
- عمل مربع كبير مساحته س2 كما في الشكل بالصفحة التالية للرسم0

- يحدد مربعا صغير مساحته ص2 ، وليكن مكعب واحد ويتم حذفه من المربع الكبير 0

- يتم حذف الجزء الأسفل من المربع الذي مساحته : ص ( س- ص )

ونضعه بمحاذاة الجزء الآخر 0

- ينتج مستطيل بعداه ( س - ص ) و ( س + ص )

فيكون ( س+ ص ) ( س- ص ) = س² - ص2

استنتاج :

حاصل ضرب مجموع حدين بالفرق بينهما=مربع الحد الاول-مربع الحد الثاني

س ² - ص ²

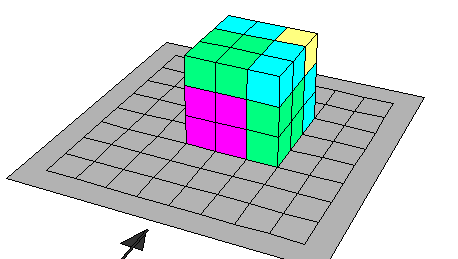
رابعـا : - مكعب مجموع حدين ( س + ص ) 3

حيث ان س الحد الاول ، ص الحد الثاني ، س= ص مجموع الحدين0

( س +ص )3 = ( س + ص) (س+ص ) ( س+ ص)

= (س + ص ) ( س+ ص)2

= (س+ص ) ( س2 + 2س ص + ص 2 )

= س ( س2 +2س ص + ص2) + ص ( س2 +2س ص +ص2)

= س3 + 2س2 ص + س ص2 + س2 ص + 2 س ص2 + ص3

= س3 + 3 س2ص + 3س ص2 + ص3

لتوضيح مفكوك مكعب مجموع حدين ( س + ص)3 نقوم بما يلي :

- بناء جسم من مكعبات س يمثل في صورة ( س + ص )3

أى يكون بعد المكعب ( س + ص)

حجمه = (س + ص) (س +ص ) (س +ص )

- نقوم بتجزأة المكعب إلى الأجزاء المطلوبة كما في الخطوات السابقة 0

- الشكل الأول س3 ويقطع من الجسم 0 فيبقي الشكل الذي أبعاده س و س و ص أي س2 ص

- ويمثل 3 قطع إذن 3 س2 ص 0

- وكذلك الجزء الآخر الذي أبعاده ص وص و س يمثل س ص2

ومكون من ثلاثة قطع أى 3 س ص2

- إذن ( س +ص )3 = س3 +3س2ص + 3 س ص2 + ص3

ويمكن أن يكون على الصورة :-

(س +ص )3 = س3 + 3س ص ( س+ ص ) + س3

تدريـب :

أوجد مفكوك ( س + 2ص ) 3

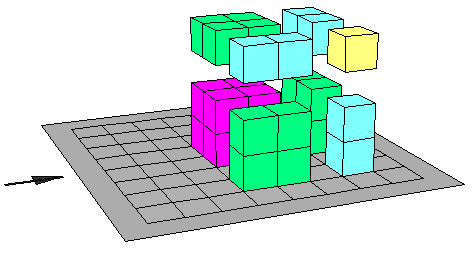
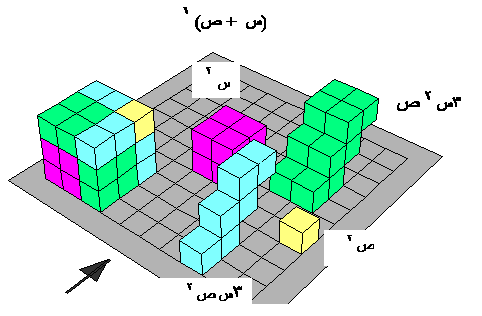
خامسـا : مكعب الفرق بين حدين : ( س - ص )3

حيث يمثل س الحد للاول ، ص الحد الثاني

(س -ص)3 = (س-ص) (س-ص) (س-ص) = ( س-ص)(س -ص)2

= (س-ص) (س2 -2س ص+ ص2)

= س(س2-2س ص+ص2) -ص(س2-2س ص+ص2)

= س3 -2س2ص+ س ص2 -ص س2 +2س ص2 -ص3

= س3 -3س2ص +س ص2 -ص3

لبيان مفكوك مكعب الفرق بين حدين ( س -ص )3

- بناء مكعب يكون طول بعده س فيكون حجمه س3

- توجد المقدار ص3 حيث يمثل مكعب صغير بعده (ص )

- نقوم بطرح ص3 وبعض الأخرى من الجسم للحصول على ( س - ص)3

- يبقي لدينا من الأجزاء س2 ص ثلاثة اجزاء 0

وكذلك س ص2 ثلاثة اجزاء وهي على النحو التالي يمكن توضيحها: 3[(س-ص)2ص]و 3ص2(س-ص)

=3(س2-2س ص+ص2)ص -3س ص2 -3ص3

= 3س2ص-6س ص2+3ص3+س ص2-3ص3

=3س2 ص-3س ص2

ويمكن تمثيلها كذلك بالصورة :

(س -ص )3=س3 - 3س ص( س -ص ) - ص3

استنتاج :

مكعب الفرق بين حدين = مكعب الأول - 3× الأول × الثاني × الفرق بين الحدين - مكعب الثاني 0

( س - ص ) ³

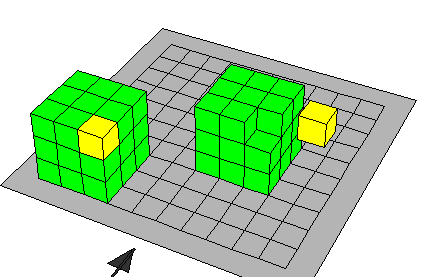
( س - ص ) ^{3 ، 3
س ص (س - ص)}

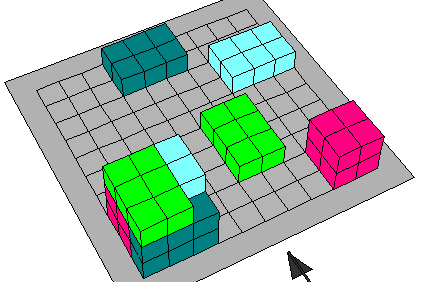
( س - ص ) ^{3 =} 3 ( س - ص ) ²ص + 3 ص ²(س - ص) + ص ²

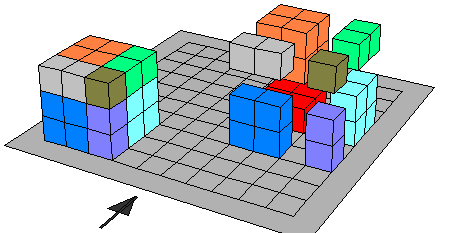
سادسـا : مجموع مكعبين ( س3 + ص3 )

حيث أن س يمثل الحد الأول ، ص يمثل الحد الثاني :

س3 +ص3 = (س + ص) (س2 -س ص +ص2 )

لايجاد مفكوك مجموع مكعبين نتبع الخطوات التالية :

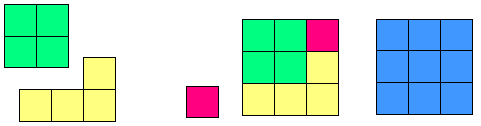
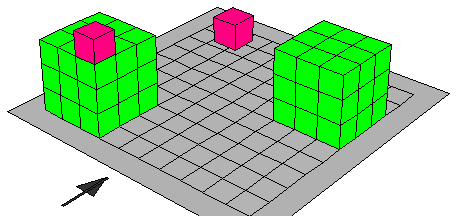
- بناء مكعب صحيحة ( س3 ) كما هو موضح بالرسم حيث ابعاده س

- يضاف المكعب الصغير ص3 على المكعب س3

فيمثل الشكل س3 + ص3

- نحدد اجزاء الشكل المطلوب على النحو التالي :

- نقتطع الشكل الذي حجمه ص2 ( س + ص )

- فك الجزء المتبقي وإضافته إلى أحد الجزئين الجوانب للشكل الباقي

فيصبح حجمه س ( س- ص) (س+ص)

وبتجميع الشكل ينتج :

س3 +ص3 = ص2 ( س +ص ) +س( س2 -ص ) (س+ص )

= س ص2 +ص3 + س( س2 -ص2)

= س ص2 +ص3 + س3 -س ص2

=(س+ص ) (ص2 + س2 - س ص) = (س+ص) (س2 - س ص + ص2 )

استنتاج :-

مجموع مكعبين = ( مجموع الحدين ) ×( مربع الحد الأول ) - حصل ضرب الحدين + مربع الحد الثاني )

س ^{3 +}ص ³

سـابعا : الفرق بين مكعبيـن : ( س3 - ص3 )

س3 -ص3 = ( س - ص) ( س2 + س ص + ص3 )

لايجاد المقدار ( س3 - ص3 ) نقوم بالخطوات التالية :-

- بناء مكعب حال بعداه (س) ، حجمه يصبـــح (س3 ) كما هو

موضح بالرسم 0

- تعيين المكعب (ص3 ) من المكعب الكبير الذي بعدد (ص) فيتكون لدينا الشكل التالي :

- تحدد المقدار بتحديد الاجزاء له على النحو التالي :

الشكل الصغير حجمه ص 2 ( س- ص )

المتبقي من الشكل يتم ترتيبه بحيث يصبح حجمه :

س ص ( س- ص ) والجزء الآخر س2 ( س - ص)

- وبتجميع الشكل الناتج يصبح المقدار على الصورة 0

س3 - ص3 = ص2 ( س - ص ) + س ص (س- ص ) +س2 (س- ص )

= (س -ص ) [ ص2 + س ص + س2 ]

= ( س- ص ) ( س2 + س ص + ص 2 )

ملاحظة :

توضح كذلك الاجزاء (س+ص ) (س-ص ) س =(س2 -ص2)س

لان (س2-ص2) س + ص2(س-ص) =س3-س ص2+س ص2-ص3 = س3-ص3

استنتاج :

الفرق بين مكعبي حدين =( الفرق بين الحدين ) × ( مربع الحد الاول + حاصل ضرب الحدين + مربع الحد الثاني )

س ³ - ص ³ =(س - ص )(س ² + س ص +ص ² )