التعابيــر الرياضيــة

                أولا :  العبارات الرياضيــة 0

                 يمكننا بواسطة استخدام المكعبات ان نوضح معنى التعابير الرياضية التي  على النحو التالي :

                ( 2)2 + ( 2 × 3 )

               على الرسم في الصفحة التالية يتبين لنا 0

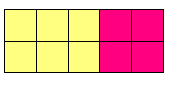
                2 × ( 2 + 3 ) يمثل مستطيل أحد بعديه ( 2) والآخر ( 2 +3 )

                فيمكن أن يفصل بحيث يوضح الجزء الأول  2× 2  +  2 ×

               أو يكتب في صورة  2( 2 + 3 ) وهذا ما يوضح معنى أخذ العامل المشترك ففي المثال السابق أخذنا العدد ( 2)

              نشــاط :

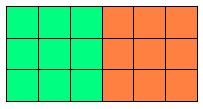
                 كيف يتم توضيح المقدار  3 × ( 3 + 4 ) يمكن باستخدام توزيع الضرب على الجمع ي كون : (3)2 + ( 3× 4 )

               وكذلك إنها تمثل العدد ( 3+ 4 ) مكررة ثلاث مرات نجد من المثالين السابقين نستطيع التعبير عن المقادير السابقة رياضيا كالتالي :

                 ن + ن + ن   = 2ن + ن      = ن( 2ن + 1)

                       فالعبارة الرياضية ، تمثل جمل لفظية عبارة عن عدد مضاف الى متغير او مضروب فى متغير ، فالمتغير يمكن تمثيله بالحرف ن بحفظ مكانا للعدد فى العبارة الرياضية والاعداد  2 ، 3 ، 4 ،000000 تمثل قيم التغير  0

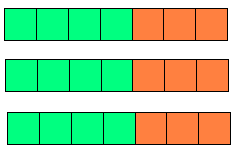
                                                                          3 ²  +  3  × 4                                                             

                3   ×   ( 3 × 4 )                                      3   ×   ( 3 × 4 )

نشـاط :

               الشكل التالي الموضح بالرسم يمثل العبارات التالية :

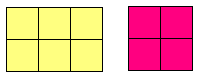
               1- (2) + ( 3 × 2 ) تمثل بالمكعبات على النحو مستطيل مكون جزء من    مربع العدد ( 2 ) = (2× 2) مضافا إليه مستطيل بعديه ( 2× 3 )

                 فيمكن ان يمثل باحد العبارات التالية :-

                 (2) + ( 3 ×2)    = 2 ( 2 + 3 )

                 2- وإذا مثلنا المقدار :

                  (3) +  ( 3 ×3 )    =  3( 3 + 3 )

             -  يمثل عبارة مربع  ( 3 × 3 ) أى (3)2  مضافا اليه العدد   (3)  مكررا

               ثلاث مرات 0

               -  وكذلك يعتير عنه بالمقدار  ( 3 + 3) مكررا ثلاث مرات

               فهذه تمثل عبارات عددية ويمكن التعبير عن هذه العبارات  العددية   بالعبارات الرياضية على النحو التالي :

                                 (2) + ( 3 × 2)

                                 (3) + ( 3 × 3 )

                                 (4) + ( 3 × 4 )

              ن + (3 ن) = ن(ن + 3 ) فهذه العبارة الرياضية  تحتوي على متغير

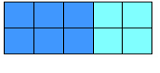
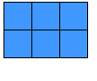
                  2 ²  +  2  × 3                2 ²     +    2  × 3

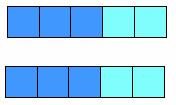
                                                    2  ×   (  2 +  3 )

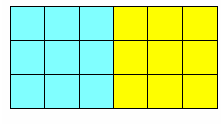
                   3 ²     +  (  3  × 3 )                   3 ²         +     3  × 3

 3      × (  3  + 3 )

                          2 ²   ×  (  2  +  3 )                       2 ³     +    3  ×   2 ²

                           3 ²   ×  (  3  +  2 )                 3 ³     +       2  ×   3 ²

              نشــاط :

               لتمثيل العبارة لعددية التالية :

             1 - (2 ) - ( 1 ) يمثل بواسطة المكعبات ويتم ذلك ببناء مربع طول ضلعه    (2)فيصبح لدينا مساحته ( 2) ، فاذا طرحـنا منه مكعب واحد مساحته (1 )

             2- يمكن اعادة ترتيب الشكل في صورة مستطيل من ثلاثة  مكعبات بعدد

                    ( 1 × 3 ) اذن  - (2) - (1 ) = ( 1 × 3 )

             نشـاط :     مثل العبارة العددية التالية : ( 3) -  ( 1 )

            1- يمثل بواسطة بناء مربع من المكعبات طول ضلعه (3) فيصبح مساحة   الشكل ( 3 × 3 )  = ( 3 )2

             2- يطرح منه مربع واحد مساحته ( 1)

              3- يتم اعادة ترتيب وبناء الشكل فيصبح لدينا مستطيل بعداه ( 2 × 4 )

                  وهكذا عند التعببر عن المقدار ( 4 ) - (1 ) = 3 × 5

               الاستنتاج :

                        من الأنشطة السابقة يمكن تحديد العبارة الرياضية على صورة متغير على النحو التالى : ن -  1 = ( ن - 1 ) ( ن + 1 )

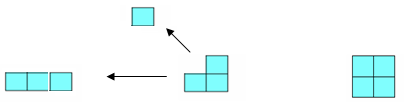
                  2 ²                    2 ²    -  1 ²           1   × 3

                   3 ²                    3 ²    -  1 ²           2   × 4

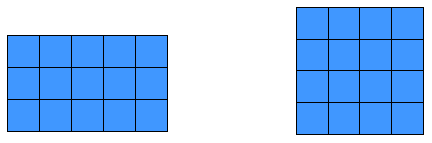
                   4 ²    -  1 ²                       3   ×  5

                نشـاط :

        مثل العبارات العددية التالية :

                1-      3  -  2

                 - بناء شكل بالمكعبات فى صورة (3× 3 ) أي مربع طول ضلعه (3)

                 - طرح الشكل الممثل 2 ويتم اعادة تنظيم الشكل 0

                 - الشكل الناتج مستطيل يعدد ( 1 × 5 )

                  2- العبارة  4  -  2

                  - بناء شكل رباعي بالمكعبات طول ضلعه (4)

                  - طرح المقدار 2 أي مربع مقداره (4) مكعبات 0

                  - يتم إعادة تنظيم الشكل فيكون مستطيل بعداه (2 × 6 )

                  النتيجــة :

                   - العبارة الرياضية تمثل في الصورة 0 ن -  2 = ( ن -2) ( ن +2)

                   - يمكن تعميم النتيجة على أن تكون :

                      ن - ع = (ن -ع ) ( ن - ع ) ، ن ، ع    ك

                     تــدريب :

                            مثل العبارة الرياضيــة : ن - 3

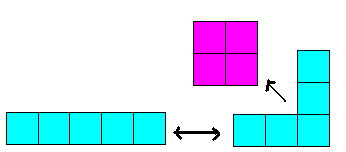
                   3 ²                          3 ²    -  2 ²              1   × 5

                   4 ²                           4 ²    -  2 ²                   2   × 6