الكســور الاعتيــادية

                  تمثل الكسور الاعتيادية جزءا أساسيا من رياضيات المرحلة الابتدائية وذلك لأهميتها في الحياة اليومية ، فهي ضرورية ، ويبدأ المفهوم الرياضي للكسور مثل تحديد نصف الشئ  أو ربعه أو مقارنة النصف بالربع 0

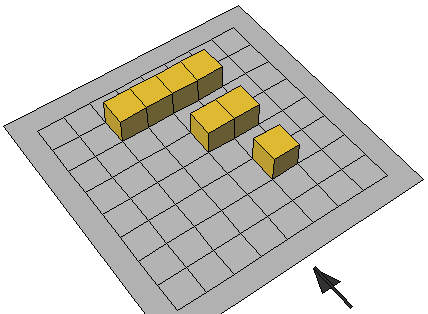
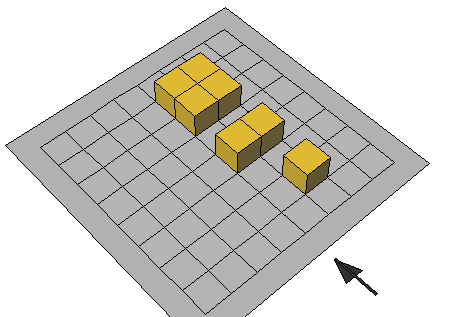
                  والتركيز عليها في المرحلة الابتدائية لهذا الفهم لابد أن يكون من خلال الأمثلة   المباشرة الملموسة والتي تلمسها التلميذة بنفسها من خلال الأنشطة مثلا باستخدام المكعبات المتداخلة يعطى التلميذة مستطيل أو مربع مكون من المكعبات ويطلب منها أن تحدد نصف الشكل 0

               فمن الامور التي يجب التركيز عليها عند التدريس للكسورأن تفهم التلميذات :-

              1- معنى الكسر وما هو الرمز 0

              2- تكافؤ الكسور 0

               معنــى الكسـر : 

                   تعنى بكسر وعلى هذا فالكسر (   ) يعنى أن شيئا كسر إلى نصفين كما تم  توضيحه سابقا وأخذ جزء واحد منها 0

              من هنا نحدد معاني للكسر منها :

              - الكسر هو جزء من كل 0

              - الكسر هو جزء أو أكثر من أجزاء متساوية من مجموعة وحدات 0

              - الكسر هو نسبة 0

              - الكسر هو دلالة على القسمة 0

      وتعطي هذه للتلميذات في المرحلة الابتدائية من الصف الثالث الابتدائي وتقدم بعد ذلك في الصف الرابع الابتدائي ، ومرحلة متقدمة في الصف الخامس الابتدائي ، وبمعنى الاعداد النسبية في المرحلة المتوسطة 0

               لتوضيح معنى الكسر :

     يعرض أحد الأشكال الهندسية وليكن المربع على مجموعة من التلميذات ، ويطلب من كل مجموعة ان تقسم المربع بالتساوي 0 على أن تكون مجموعة من  ، 2 ، 4 تلميذات 0

                 وبالمناقشة يتم التوصل إلى أن الجزئين نقول نصفان أي واحد من اثنان فهو نصف  المربع ويكتب :

               وبعد ذلك نعيد المناقشة مع المجموعة الثانية المكونة من أربع تلميذات أي الجزءالواحد يقرأ :

               - واحد من أربعة 0

               - ربع ، فيكون واحد على أربعة 0

                   ويوضح أن أربعة أرباع تكون واحد وتكتب (    ) وهذا يوضح المفهوم جزء من كل

                    فاذا أخذ جزئين من الاربعة أجزاء يقال  " ربعين اثنين من المربع،وبعد ذلك يوضح     ثلاثة أرباع 0

                 ويتم توضيح ذلك بالرسم في الصفحة التالية من خلال عرض الدرس 0

              ملاحظــة :

                  يتم توضيح البسط والمقام في الكسر حيث عدد المكعبات بلون محدد يسمى  البسط     وعدد المكعبات الكلية يسمى المقام 0   

            1        ،       1 /  4      ،    1 /  2                      1        ،       1 /  4      ،    1 /  2

       1 / 5    ،       2 /  5      ،       3 /  5                                  3 /  4      ،       4 /  6  +  2 / 6 

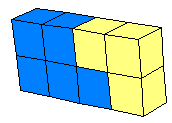
                               4 / 8             ،             3 /  8               ،             5 /  9

              نشـــاط :

              الهـدف : مقارنة كسور الوحدة بوضع اشارة (  >  ،    < ،   =   ) باستخدام المكعبات المتداخلة ذات الألوان المختلفة 0

             - يوزع التلميذات على مجموعات وباستخدام المكعبات يطلب تحديد الكسور      المختلفة : (    ،     ،      ) 

             - وبالمناقشة مع مجموعة التلاميذ المكونة من اثنين ، فهنا يوضح الجزء الواحد يعنى  نصف أى العدد واحد من اثنين 0

             - وتعاد المناقشة مع لمجموعة المكونة من 3 تلميذات ، كما في الشكل على المكعبات ، حيث يبين واحد ثلث أي أن الشكل جزء إلى ثلاثة أجزاء وأخذ منها واحد جزء 0

               وعند أخذ اثنين يكون اثنين ثلث وهكــذا 0

               وهنا تكون المناقشة مع التلميذات 0

              - ماذا يعنى العدد ( 1) والعدد ( 2) في الكسر  (   ) ؟

              - ماذا يعنى العدد ( 1) والعدد ( 3) في الكسر (   ) ؟

                وبمقارنة النصف بالثلث يطرح السؤال 0:

              - النصف أم الثلث أكبر ؟

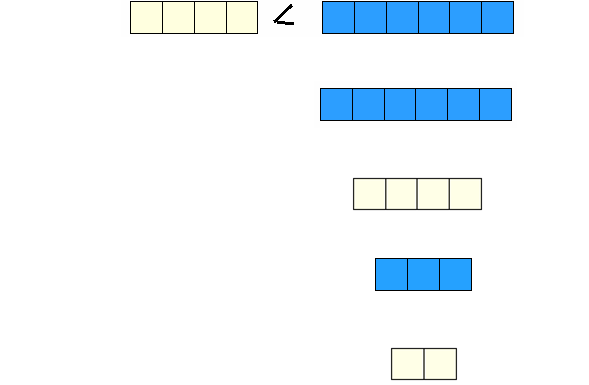
نشــاط :

             مضاعفات كسور الوحدة هي الكسور الاعتيادية التي بسطها أكبر من الواحد0

            الهـدف :

            التعرف على مضاعفات كسور الوحدة مثلا :

               (     ،      ،    0000000000 ،     )

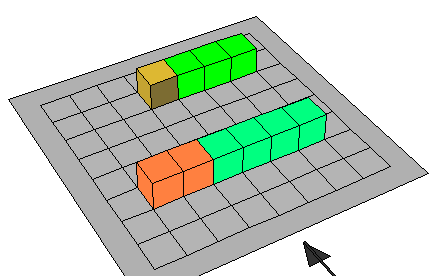
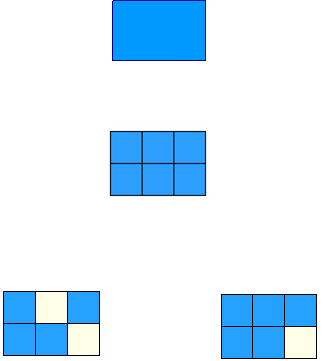
            تستخدم المكعبات المتداخلة نقوم ببناء مستطيل من سته مكعبات وتبدأ     

            المناقشة مع التلميذات لإيضاح ذلك 0

                 - هل يمكن تجزئة هذا المستطيل ؟

                 - إلى كم جزء يمكن أن يقسم ؟

           فهنا نبدأ بإبدال اللون الأبيض من المكعبات بلون مغاير لاجزاء على أساس أنه يتم

           تقسيم المستطيل إلى ستة أجزاء متساوية 0

              - فالجزء الواحد هو  (    ) يعنى واحد من ستة 0

              - ونكتب السدسان بالرمز (    ) وهكذا نتوصل الى ان :

                                      (      ،      )

          تطبيـــق :

    الكسـور المتكافئة

                تكافؤ الكسور مفهوم أساسي لفهم الكسور ، وتنمية هذه الفكرة من خلال ممارسة الأنشطة من قبل التلميذات ومناقشتها معهم بشكل عملي 0

                نشــاط :

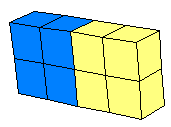
              الهــدف : أن تدرك التلميذات مفهوم التكافؤ ( الكسور المتساويه ) تستخدم المكعبات في توضيح ذلك من خلال عرض مربعات متساوية في المساحة ، ويبين فيها تجزئ الأنصاف والأرباع 0

                  يبين الشكل الأول يمثل : (    ) المربع   ، والشكل الثاني (    ) الشكل اثنين على أربعة وبالمناقشة من خلال الشكل نقارن المساحة بين الشكلين 0

              مساحة نصف المربع بمساحة ربعي المربع 0

                ويعرض بمجموعة أخرى من التمارين على هذه نجد أن :

                                (     )  =   (     )

                                (     )  =   (     )

                                (     )  =   (     ) كما هو موضح فى الرسوم التالية 0

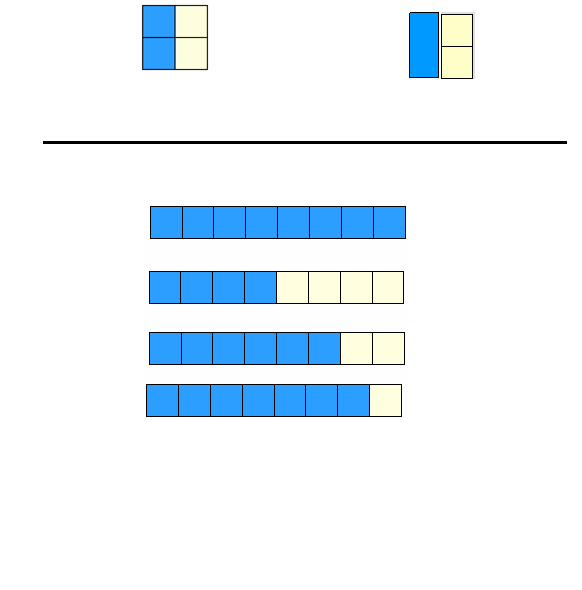
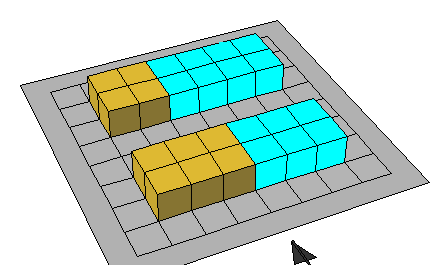                           2  /  3      >       1  /  2 

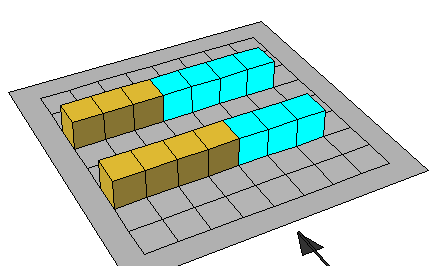                           4  /  7      >       3  /  7 

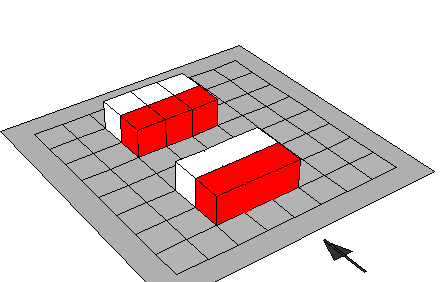                    1   /  2     =       3  /  6 

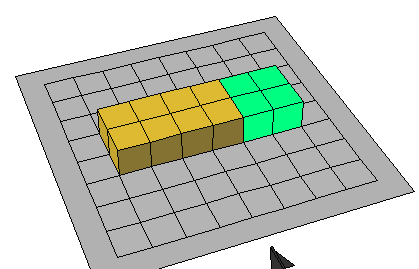                             1  /  3     =       4  /  12 

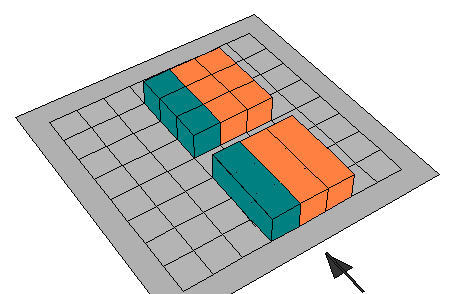               2  /  3     =       6  / 9

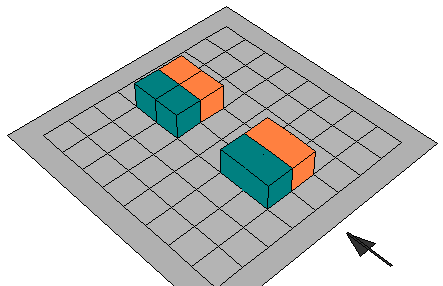                 1  /  2     =       2  /   4

 العمليات على الكسـور

             أولا :  جمع الكسور : 

             ان اجراء عملية الجمع للكسور التي لها نفس المقام ، انه ينتج كسر له نفس المقام

            وتختلف جمع الكسور عن جمع  الأعداد  الكلية 0

             نشـاط :  

            جمع كسرين لها المقام نفسه 0

                    أجمع   (    )  +  (     )

              حتى يعطى للتلاميذ مكعبات بحيث يتم تكوين مستطيل ( 5 × 1)

              ويمثل : (     ) و (     )   فان الناتج  (    )

              وعند إعطاء مثال آخر : 

              (    ) + (    ) + (    ) يعرض كما هو في الرسم بالصفحة التالية 0

              فيكون الناتج   (    )

              وإعطاء أمثلة أخرى :  (    )  +  (    )     و    (    )  +  (    )

             *  جمع الكسور مختلفة المقام :

               يعرض الشكل من المربعات الخطوة (1) 0

             1- عند تغطية (    ) الشكل بالمكعبات الزرقاء ، فما هو عدد المكعبات 0

             2-  عند تغطية (    ) الشكل بالمكعبات الحمراء ، فما هو عدد المكعبات 0

             3- (    ) الشكل  + (    ) الشكل  = 7 مكعبات 0

                  أذن (     )  +  (     ) =  (     )  +  (     )  =  (     )

                 ثانيـا: طـرح الكســور :

               الطرح يشبه الجمع 0

                 لتوضيح فكرة الطرح مثلا لدينا مكعبات نكون بها مستطيل بعداه ( 3 × 2) كما هو في الشكل التالي :

              - وتحدد (    ) الشكل باللون الأحمر 0

              -  تحديد عدد الكسور المقتطعة من الشكل 0فهى تمثل (    )

              - نلاحظ الكسر المتبقي الذي يمثله الجزء الملون باللون الأحمر 0

               فيكون (    )  -  (    )   =  (    )

                الاستنتاج :

             1 - الفرق بين كسرين لهما مقام مشترك هو الكسر الذي بسطه يساوى الفرق   بين     بسطى الكسرين ، ومقامه نفس المقام 0

تمـرين : 

                  تمثل العملية حسب الشكل (2)  :  (     )  -  (     )

             2- طرح كسرين عملية عكسية لجمعهما كما فى المثال التالي :

                               (    )  +  (    )  =  (    )

                               (    )  -  (    )  =  (    )

                    وكذلك : (    )  -  (    )  =  (    )

                            وهذا موضح بالرسم في الشكل التالي :-

                 ثالثـا: ضـرب الكسـور  

                   قد تبدو عملية الضرب في الكسور سهلة لأنها تبني على أساس ضرب  البسطين وضرب المقامين ، ولكن ربما التلميذات يتعرضن الى النسيان ، ولكن باستخدام اجراءات الضرب بطريقة ملموسة أمام التلميذات فهنا يمكن استنتاج القاعدة بانفسهم 0

              أ- ضرب كسر بعدد0  لتوضيح ذلك نقوم بخطوات 0

                   خطوة ( 1) : تمثل الأعداد بواسطة المكعبات بحيث يمثل الشكل (1) وحدة               وأردنا تحديد (     ) كل واحد منها 0 

               إذن يكون (     ) الأول + (     ) الثاني +  (     ) الثالث  =  (    )

              ويمكن القول بالمناقشة مع التلميذات بان (    ) الثلاثة 0

              أي (    )  ×  (     )  =   (        )   =  (     )

              مثال :   أوجد = (     ) العدد (     )

               تمثل العدد ( 2) بمربعين يقسم كل مربع إلى أربعة أقسام 0

             وتحدد(    )كل عددكماهوموضح بالرسم بواسطة المكعبات فى الصفحة التالية :-

             ويمكن كذلك فهو         العدد  3 

             أن نستنتج أن :      ×   2  =       =     

                  من المثالين السابقين يفهم التلميذ معنى الضرب ، ويمكن أن تستخدم الجمع      المكرر وينتج انه يمثل      ×  2 =       

نشـاط :  

              أوجـد (     ) العدد  6

               الحـل :  

               من الرسم ينتج إننا يمكن أن نمثل العدد بواسطة المكعبات على أساس أن العدد

              يمثل سلسلة من المكعبات كما هو واضح في الرسم 0

              فيتكون العدد ( 6 ) وتحدد (   ) كل عدد و (    ) فيصبح (    ) العدد التى تمثل اللون الأزرق في كل عدد0

              فيكون (    )  +  (    )  + (    )  +  (    )  +  (    )  +  (    )  =  (   )

              فنجد ان  :   (    ) ×  (    )  = (        )   =  (     )

              تطبيــق :

              - أوجدي حاصل ضرب (    )  ×  (     )  ونعنى أربعة أنصاف 0

                 ب - ضــرب كسـر بكسـر 

                  لتوضيح فكرة ضرب كسر بكسر على انه ضرب بسط الكسور في بعضها فنحصل على البسط وضرب المقامات للكسور نحصل على مقام الكسر 0

                نشـاط: 

                لضرب (    )  ×  (    ) توضيح أنها ثلث النصف أو نصف الثلث 0

                  لاجراء عملية الضرب  يتم توزيع مستطيلا مكون من المكعبات على مجموعة من التلميذات بعداه ( 3  × 2) ويتم الخطوات التالية كما هو موضح بالرسم 0

               - يتم تحديد نصف المستطيل باللون الأحمر اذن يتصل (    ) المستطيل 0

               - تأخذ (    ) النصف المحدد لدى التلميذات - كما هو في الخطوة التالية  الموضحة بالرسم في الشكل 0

               - نلاحظ الناتج يمثل مكعب واحد وهو (    ) الشكل الكلى 0

                وتتم المناقشة لتحديد (    ) ما هي عدد الأجزاء المساوية للمكعب في   المستطيل الكامل 0

                   فهنا نستنتج إن العملية التي أجريت على بسطي الكسرين (    )  ،  (    )  

                  هي : (    )  ×  (    )  =  (        )  =  (    )   ( نصف المثلث )  

                نشـــاط :

               أحسب (    )  ×  (    ) كما هو موضح فى الشكل فى بالصفحة التالية :

               - يحدد نصف المستطيل (   ×    ) تمثل بعدا المستطيل 0

               - يحدد (   ) النصف ، ولا بد ان يحدد مسبقا عدد الإجزاء الكلية للشكل          المساوية لـ (    ) الشكل 0

                - نحصل على الناتج (     )

                 تطبيقــات :

                   أوجد :- (     )  ×  (     )

                             (     )  ×  (     )

                             (     )  ×  (     )

قســمة الكســور

                  قســمة كسر على عدد:

            ان فهم التلميذات لعملية قسمة الكسور تعتمد غالبا على مدى فهمهم    لفكرة القسمة فهما صحيحا ، لذلك لابد تمثيل العدد في شرح القسمة إن يتم توضيح ومناقشة معنى القسمة على سبيل المثال ( 20 ÷ 5) فيمثل ذعدد المجموعات التي عدد عناصرها (5) أشياء ويمكن ايجادها من عناصر (20)  (أو كم 5 توجد في 20)

              فيمكن البدء حول قسمة الكسور مثلا ( 1 ÷    ) وهكذا  

             على أنها كم نصف تكون واحد صحيح ، فهنا تكون الإجابة     توضيح ذلك بواسطة المكعبات 0

               نشــاط :

              تم تقديم قسمة كسر على عدد بان يتم تقسيم التلميذات إلى           مجموعات بحيث يكون كل مجموعة بها أربعة التلميذات0

              - يوزع على كل مجموعة أربعة مستطيلات بحيث يكون مجزأ الى  ثلاثة  أرباع كما هو موضح فى الرسم( يكون باللون الأخضر )

             - يطلب من التلميذات تقسيم المستطيل بحيث يكون مجزأ بين  شخصين وتتم المناقشة مع التلميذات ، الى كم جزء قسم الربع الأخضر والاجزاء الباقية

             فينتج انها مجزأة إلى ستة أجزاء  ويأخذ كل شخص  من الثلاثة  أرباع الخضراء (    )

              إذن عملية القسمة : (    )  ÷  (     )  =  (    )

             مع المناقشة نستنتج التلميذات ان القسمة عملية عكسية للضرب

             فيكون :   (    )  ×  (    )  =  (    )     ( أي الضرب  بمقلوب العدد)

            تطبيـــق :

 (    )   ÷  (    )    =   (     )  ×  (    )   =  (    )  أو (    )