عمليات الحسـاب الأساسية

عمليات الحسـاب الأساسية

القواعد الأربعة للأعداد الصحيحة

(الجمع - الطرح -الضرب - القسمة )

عمليتي الجمع والضرب والعمليتين العكسيتين لهما الطرح والقسمة تسمى هذه بالعمليات الأربع ( العمليات الأساسية ) وذلك لأنها تشكل أساس دراسة الرياضيات في المرحلة الابتدائية والمراحل اللاحقة لها 0

ويتعرف من خلالها على الإشارات 0

( + ) تعنى الجمع أو زائـد 0

( - ) تعني الطرح أو ناقص 0

( × ) تعني الضـرب أو في 0

( ÷ ) تعني القسمة أو على 0

ولابد أن نحتاج إلى أن تفهم التلميذات الأفكار التي وراء تلك العمليات ولا يقتصر على إجراء تلك العمليات ، لأنه يمكن أن تجري التلميذة عملية الجمع ولكن ليس ذلك دليلا على فهم الجمع 0

فتقديم عملية الجمع والطرح على أنها إتحاديين مجموعات منفصلة ، تتعرف التلميذة من خلالها على عملية الجمع 0

وبنفس الطريقة ، يمكن للتلميذة أن تعرف عن طريق الفرق بين المجموعات

المنفصلة على عملية الطرح 0 وتعرف الطرح على انه العملية العكسية لعملية الجم ومن الوسائل المفيدة في ذلك التي تساعد على تطور استيعاب التلميذ لمفهوم عمليتى الجمع والطرح هو استخدام المكعبات المتداخلة ، لأنه من خلالها يستطيع التلميذة أن تفهم عملية الترابط بين المجموعات بشكل محسوس عند عرض المعلمة لها ذلك وتوضيحه 0

ويجب أن تعطي تعريفا لكل عملية تجريها وعلى التلميذة أن تتعرف على عناصر كل عملية 0

* الجمـــع

يكون عند إضافة كمية إلى كمية أخرى من إعداد أو أشياء على أن تكون من نفس النوعية ، فنكون قد جمعنا عددين أو شيئين 0

وكمثال عند إضافة مجموعة من المكعبات إلى بعضها فهذه طريقة سهلة ومباشرة وتوضح للتلميذة ذلك بشكل مباشر 0

درس ( الجمـــع )

( الصف الأول الابتدائي )

الأهــداف :

- أن تربط التلميذة اتحاد مجموعتين منفصلتين بعملية الجمع 0

- توضيح مفهوم الجمع وربطه بمعني إضافة عدد إلى عدد0

يعطي للتلميذ مجموعتين من المكعبات ، المجموعة الأولى تحتوي على (3) مكعبات والمجموعة الثانية تحتوي على (4) مكعبات ، ويطلب منها أن تضعها في مجموعة واحدة ، وهو لديه فكرة العدد فيجمعها فيكون لديه (7) مكعبات كما هو موضح في الرسم في الصفحة التالية 0

* الطــرح

ويعني إنقاص رقم أو كمية ، فمـثلا إذا أخذنا مكعبين من خمسة مكعبات فانه يتبقى لدينا ثلاثة مكعبات 0

كما هو وأضح في الرسم في نفس الصفحة 0

وهنا كذلك الهدف هو أن تتعرف التلميذة على الإشارات + و - و =

والتمييز بينهما 0

وكذلك إن تتعرف على كتابه الجمل : أ + ب = جـ

حيث ( أ ) المجموعة الأولى ، ( ب ) المجموعة الثانية ، (جـ ) ناتج الجمع 0

كما في دروس الطرح في الصف الأول الابتدائي 0

ويمكن كذلك تعليم الطرح بالاكمال

4 + 5 = 9

درس ( الطرح بالإكمـال)

( الصف الأول الابتدائي )

الأهـــداف :

استعمال الطرح لكي توصف التلميذة عملية إكمال مجموعة لتكافيء مجموعة 0تم توزيع على التلميذات مجموعات مختلفة العدد من المكعبات المتداخلة ، بحيث لا يزيد عدد المجموعة الواحدة من (9) عناصر ، وهنا تبدأ التلميذة مقارنة عدد عناصر مجموعتها مع عدد عناصر مجموعة زميلتها 0

وتبدأ المعلمة بطرح الأسئلة على التلميذات بحيث توضح المجموعات ذات العناصر الأقل على عدد عناصر المجموعة التي تلزم للحصول على مجموعة عدد عناصرها يساوى عدد عناصر مجموعة زميلتها 0

وذلك يطرح السؤال : كم يلـزم ؟ وكم تحـتاج ؟

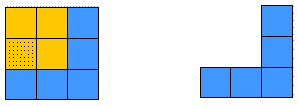
- مثلا : إذا كان لدى التلميذة الأولى مكعبين فيسأل عن كم يلزمها ليكون العدد (7) فهنا يضيف من زميلها (5) مكعبات 0

فيصبح 7 - 2 = 5

ويوضح ذلك الرسم التالي:

7 - 2 = 5

9 - 5 = 4

9 - 6 = 3

حقائــق الجمع والطرح

لتعليم حقائق الجمع والطرح هناك طرق كثيرة 0

لكل حقيقة جمع يمكن أن تربط بينها وبين حقيقة الطرح 0

فمثلا حقيقة الجمع كما يتم شرحها في درس : حقائق الطرح في الصف الثاني الابتدائي 0

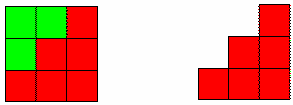
8 + 6 = 14 ، يمكن أن نربطها بحقيقة الطرح : 14 - 6 = 8

كما في الرسم في الصفحة التالية : وكذلك 14- 8 = 6 وهي ما يكون في مستويات متقدمة في الصف الرابع الابتدائي ما يتعرف عليه التلميذة 0

المطروح و المطروح منه و الباقي 0 ويمثل العلاقة 0

المطروح + الباقي = المطروح منه 0

المطروح منه - الباقي = المطروح 0

14 - 6

14 - 8

خواص الجمـــع

نستطيع اختصار حقائق الجمع وذلك بان تطبق بعض خواص الجمع ، ومن أشهر هذه الحقائق خاصية الترتيب ، خاصية التبديل في الجمع 0

يعـني ذلك أن ترتيب المجاميع لا يؤثر على نتائـج الجمع 0 وهو ما يعبر عنه بالشكل التالي :

حيث أ تمثل مجموعة من المكعبات ، وب مجموعة من المكعبات 0

فان : أ + ب = ب + أ

- مثلا : أ يمثل 4 مكعبات ، ويضاف إليها 3 مكعبات 0

4 + 3 = 7

وإذا تم جمع 3 مكعبات مع 4 مكعبات كان الناتج نفسه 7 مكعبات اى3 + 4 = 7 وهكذا إذا أعطيت أمثلة متعددة 0 كاما في الرسم فى الصفحة التالية:

فهنا تستطيع التلميذة أن تميز بان جمع عدد بترتيب معين سيكون له نفس الناتج إذا ابد لنا الترتيب 0 وذلك كما في شكل (1)

هناك خاصية أخرى للجمع وتسمى التجميع في الجمع ونعبر عنها كالتالي :

أ و ب و جـ مجموعة من المكعبات الملونة حيث كل حرف يمثل عدد معين

من هذه المكعبات كالتالي :

( أ + ب ) + جـ = أ + ( ب + جـ )

وتستعمل هذه الخاصية عندما يراد جمع أكثر من عددين ، يعطى في الصف الثاني الابتدائي درس التجميع 0

مثال : - 5 + 3 ـــ سؤال

( 3 + 2 ) + 3 ـــ إعادة تسمية

3 + 2 + 3 = ـــ جمع

3 ( 2 + 3 ) = ـــ إعادة تسمية

أذن يمكن القول بان الجمع والطرح يمثلان نصف العمليات الأساسية ، لهذا لابد أن يتم تقديمها بشكل كبير في المرحلة

الابتدائية ، وان يتم في مراحل

2 × ( 3 × 4 )

( 2 × 3 ) × 4

( 3 + 2 ) + 3

3 + ( 2 + 3)

* - الضـرب :

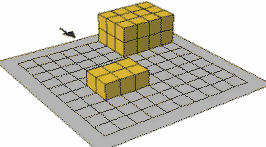
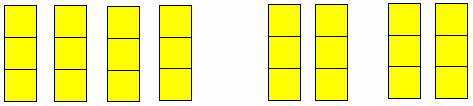
تعتبر عملية الضرب أسرع طريقة لجمع أعداد متساوية ، فيمكن النظر إليها على إنها عملية جمع مكرر لمجموعات جزئية متكافئة 0

- مثلا : 2 + 2 + 2 = 6

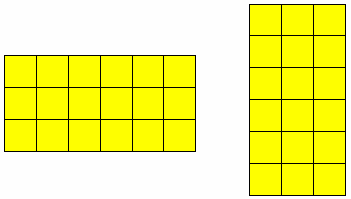
فيمكن التعبير عنها 2 × 3 = 6 أي أن العدد 2 مكرر ثلاث مرات أو أن الثلاثة مكررة مرتي 0 ويكن تمثيلها بالمكعبات المتداخلة حيث يوضح للتلميذة معنى الضرب عن طريق الجمع المكرر 0 فيعرض العدد 2 يمثلا مكعبين ، اثنين اثنين اثنين 0 فعند جمعها تعطي ستة مكعبات 0

فنتج لدينا مستطيل فنجد إن عدد الصفوف 2 من ثلاث مكعبات أو ثلاثة

صفوف من مكعبين 0

فهنا ليس من الضروري الترتيب ، مما سبق يمكن أن نقول بان :

2 × 3 = 3 × 2 = 6

أي أن 2 صفوف × 3 أو 3 صفوف × 2 وهذا ما يطلق عليه الابدال في عملية الضرب0

وهو ما يعبر عنه بالعلاقة أ × ب = ب × أ 0

ومن الأمثلة على ذلك : 3 × 5 = 5 × 3 = 15

6 × 2 = 2 × 6 0000 وهكذا كما في الصفحات التالية لرسم0

ملحوظــة:

وهذا يدرس في الصف الثاني الابتدائي0

وتعطى كذلك ضرب الستة في الصف الثالث الابتدائي 0 فالهدف منه توضيح

عن طريق العدد 6 استنتاج جدول الضرب للعدد 6بحيث يكون ستة سعة وهكذا

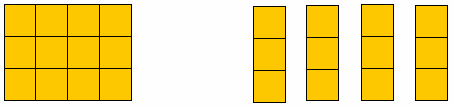
فهنا يطلب من التلميذة أن يقوم ببناء ست مكعبات ، وتكررها كمجموعات ستة ستة 0

- فيكون المستطيل الأول 6 × 1

وبعد ذلك تضيف الى المستطيل الاول المستطيل الثاني المكون من ست مكعبات فيصبح مستطيل : 6 × 2 وهكذا0

- ويكون الشكل التالي عبارة 6 × 3

فهنا يوضح للتلميذة جدول الضرب الخاص بالعدد 6 وبالتالي يمكن أن يكمل الاعداد0

- وهناك خاصية أخرى للضرب وهى التجميع كما سبق وذكرنا في ( الجمع أي تحقيق العلاقة ) أ × ب × جـ = ( أ × ب ) × جـ = أ × ( ب × جـ)

2 + 2 + 2 = 2 × 3

2 + 2 + 2 + 2 = 2 × 4

2 + 2 + 2 + 2 + 2 = 2 × 5

3 + 3 + 3 = 3 × 3

3 + 3 + 3 + 3 = 3 × 4

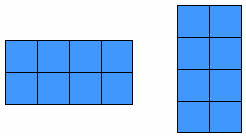
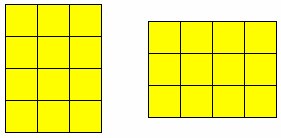
4 × 2 2 × 4 3 × 4 4 × 3

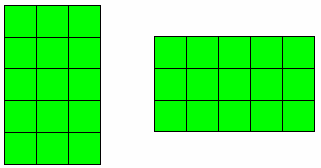
6 × 2 2 × 6 3 × 5 5 × 3

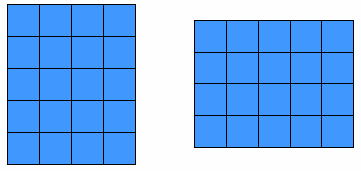
4 × 5 5 × 4 6 × 3 3 × 6

1 × 6 1 × 6 6 × 2

6 × 1 6 × 2 6 × 3 6 × 4

4 × 2 × 3 4 × 2 × 3

4 × 6 = 24 8 × 3 = 24

2 × 2 × 4 2 × 2 × 4

2 × 8 = 16 4 × 4 = 16

* - القســمة :

القسمة هي عملية تجزئة إلى أجزاء متساوية ، وتعلم بان عملية القسمة هي العملية العكسية لعملية الضرب 0

ويمكن تقديم القسمة في صورة طرح متكرر ، وذلك يتجزئ مجموعة من المكعبات إلى مجموعات جزئية متساوية ( التقسيم بالتساوي ) 0 ولاننا سبق وأن عرفنا بان الضرب جمع متكرر وهى العملية العكسية 0

فهنا فيظهر إلى القسمة على أنها 0

- أوبيان ذلك بالمثال الذي يعرض في الصفحة التالية :

16 ÷ 4 يكون 16 - 4 = 12 1

12- 4 = 8 1

8 - 4 = 4 1

4 - 4 = 0 1

إذن تكون لدينا 4 مجموعات كل منها من 4 عناصر 0

ويمكن كذلك أن تكون طريقة التقديم أن يستخدم التلميذات 10 مكعبات ويطلب من أحدهمن تقسيمها بالتساوي على 5 تلميذات اخريان فتبدأ تعطي كل تلميذة واحد مكعب ، تجد نفسها انه يمكن القيام بالعملية مرة أخرى بذلك تكون قد أعطت كل تلميذة 2 مكعب 0

فهنا يوضح للتلميذة عناصر عملية القسمة 0

المقسوم المقسوم عليه ( القاسم ) خارج القسمة

10 ÷ 5 = 2

ويمكن ربط الضرب بالقسمة : بعد أن يقوم التلميذات بالعمليات السابقة للقسمة فيكون لديهن الوعي بالعلاقة بين الضرب والقسمة 0

نفس المثال السابق 10 ÷ 5 = 2 أو 5 × 2 = 10

10 ÷ 2 = 5 أو 2 × 5 = 10

( ويمكن تدريس ذلك في الصف الرابع الابتدائي )

حيث يتم تعريف التلميذات لكيفية قسمة عدد على عدد كما سبـق توضيحه و يمكن ان يكون قسمة مع باقي أو قسمة بدون باقي 0

مثال : أوجد ناتج قسمة 11 ÷ 3 ويتم توضيح ذلك باستخدام المكعبات

المتداخلة ( الملونة ) 0

- يوضـح للتلميـذات عند قسمة تقوم بعمل مجموعات بحيث يكون كل مجموعة 0

تحتوى على 3 مكعبات ونجد انه يوجد فيها 3 مكعبات فيكون المربع 3 × 3 ويتبقى لدينا 2 مكعب لا يمكن دخولها في المجموعة فيمثل هذا الباقي 0

فيكون (11 المقسوم) و (3 المقسوم عليه ) و ( 9 خارج القسمة) و(العدد 2 يسمى الباقي) 0 وذلك يوضح في الرسم التالي:

16 16÷ 2 = 8

16 ÷ 4 = 4

11 ÷ 3

المقسوم =المقسوم عليه × خارج القسمة + الباقي

خارج القسمة الباقي