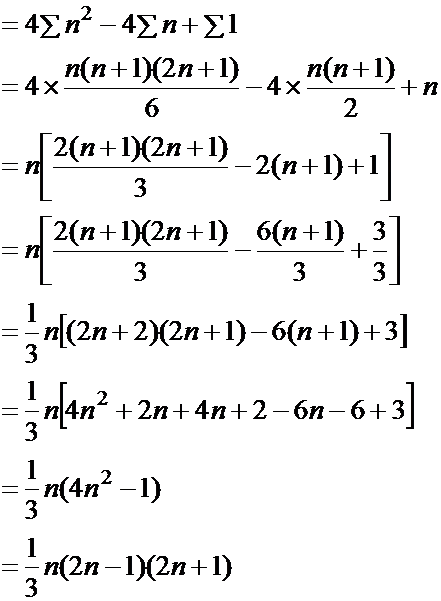|
الحد النوني للأعداد الفردية
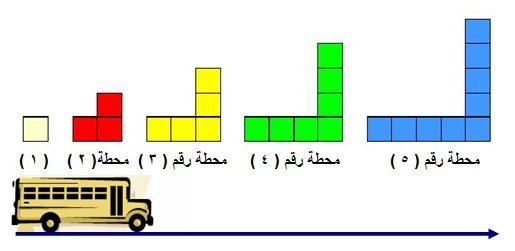
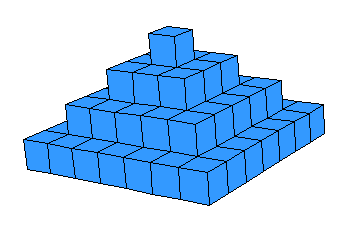
مثال : تتحرك إحدى الحافلات وتمر في طريقها بعدد من المحطات . فإذا ركب في المحطة الأولى راكب واحد ، وفي المحطة الثانية ركب ثلاثة ركاب ، وفي المحطة الثالثة ركب خمسة ركاب ، ثم استمرت الحافلة في سيرها إلى محطات أخرى ؛ وكان عدد الركاب يزيد في كل محطة بالوتيرة نفسها . فكم تتوقع يكون عدد الركاب في المحطة العاشرة ؟ . كما هو موضح في الشكل التالي :
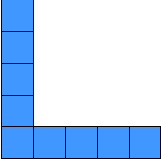
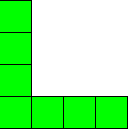
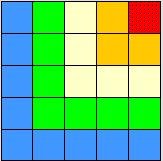
الحل : نلاحظ أن هذه العملية تمثل متتابعة حدودها الأولى ، هي :1، 3 ، 5 ، 7 ...... ومن الواضح أنها متتابعة حسابية ، حدها الأول = 1 ، وأساسها = 2 . ولكي نوجد عدد الركاب في المحطة العاشرة ؛ فلابد أولاً من إيجاد الحد النوني لها ، ويمكن ذلك بأكثر من طريقة : الطريقة الأولى : من خلال شكل التمثيل البياني للحدود: ويتم بمحاولة اكتشاف النمط الذي تسير عليه هذه المتتابعة ، وهو ما يعني رياضياً إيجاد الحد النوني لها ، وعندما نتأمل في هذه الحدود سنجد أن كل حد منها يتكون من :
من خلال الجدول نلاحظ أن عدد الركاب في كل محطة عبارة عن العدد ( واحد ) مضاف إليه جزئين كل منهما عبارة عن ( رتبة الحد مطروح منها العدد واحد ) . وبالتالي فإن : الحد في هذه المتتابعة = مربع واحد ثابت ( كما في شكل التمثيل البياني ) + جزئين متغيرين كل منهما يساوي رتبة الحد مطروح منه واحد ) . ( ومن الواضح أن عدد المربعات في كل جزء = رتبة الحد -1 ) وبالتالي : ح ن = 1 + 2 ( ن-1 ) ح ن = 1 + 2 ن-2 ح ن = 2 ن - 1 والآن يمكن إيجاد عدد المربعات في الحد العاشر كما يلي : ح 10 = 2 × 10 -1 = 19 راكباًً .
الطريقة الثانية : باستخدام القانون العام لإيجاد الحد النوني للمتتابعة الحسابية : ح ن = أ + ( ن - 1 ) د حيث : أ هو الحد الأول ، د هو أساس هذه المتتابعة أ = 1 ، د = 2 ح ن = 1 + 2 ( ن - 1 ) = 1 + 2ن - 2 ح ن = 2ن -1 والآن يمكن إيجاد عدد المربعات في الحد العاشر كما يلي : ح 10 = 2 × 10 -1 = 19 راكباً .
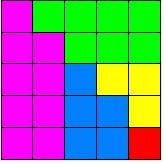
مربع الأعداد الفردية مثال 1 : ليكن لدينا الشكل التالي:
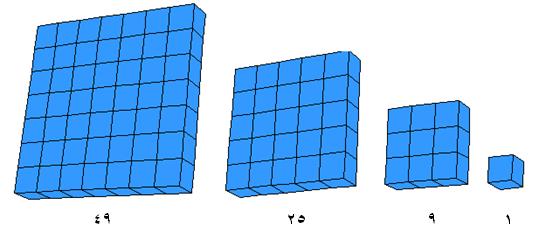
أوجد الحد العام للمتتابعة التي يمثلها هذا الشكل ، ثم أوجد مجموع هذه المتتابعة ؟ الحل : نقوم بفصل كل حد من حدود هذه المتتابعة عن الآخر ، سيكون شكل هذه الحدود كما يلي :
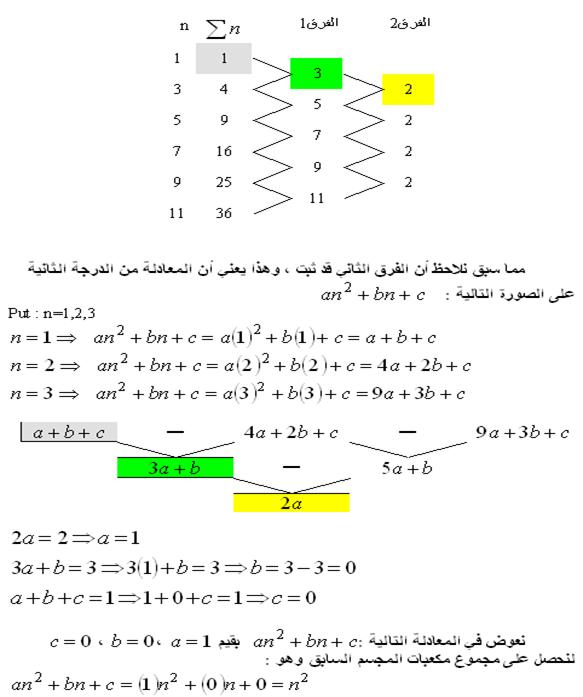
نحدد أبعاد كل حد . سنجد أن : 1 = 1×1 9 = 3×3 25 = 5×5 49 = 7×7 نتأمل هذه الحدود من خلال الجدول التالي :
وعليه فإنه من الواضح أن حدود هذه المتتابعة هي مربعات الأعداد : 1 ، 3 ، 5 ، 7 ، .... على الترتيب . وهذه الأعداد هي الأعداد الفردية ، فتصبح هذه المتتابعة هي مربعات الأعداد الفردية . الآن وبعد أن تعرَّفنا على الحد النوني لهذه المتتابعة تكون إجابة السؤال السابق بإيجاد مجموع مربعات الأعداد الفردية ، كما يلي :
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||