|
متتابعة
رقم 18
س4)
أوجد الحد النوني للمتتابعة الموضحة بالشكل الآتي؟ ثم أوجد المجموع النوني
لهذه المتتابعة؟
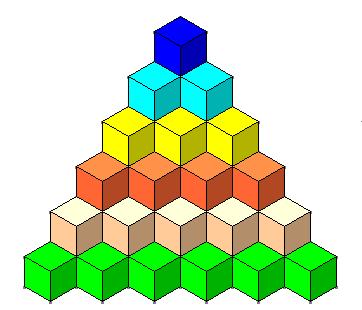
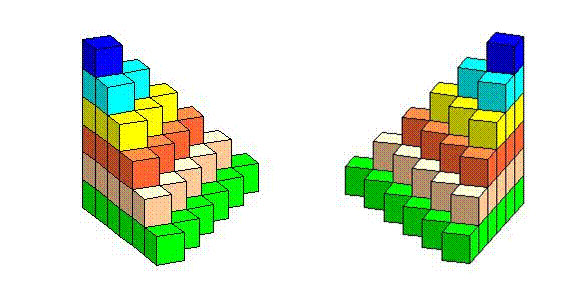 الشكل
كامل الشكل
كامل


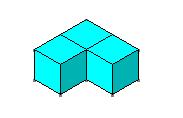 الحد
الأول الحد
الأول

الحد الثاني
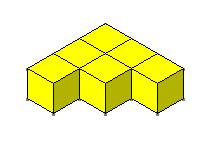

الحد الثالث
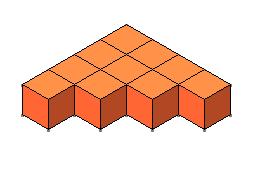

الحد الرابع
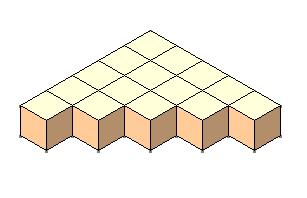

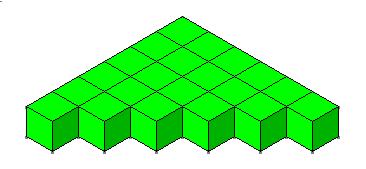 الحد
الخامس الحد
الخامس

من
الممكن استنتاج قاعدة النظام ببناء جدول توضح فيه
الدور وعدد المكعبات
ومحاولة الربط بين العددين
|
|
مكعبات |
n |
|
|
1 |
1 |
|
|
|
3 |
2 |
|
|
|
6 |
3 |
|
|
|
10 |
4 |
|
|
|
15 |
5 |
|
|
|
21 |
6 |
كيف نصل
من 6 الى 21
كيف نصل
من 5 الى 15
بعد
محاولات يكتشغ الطالب العلاقة بينهما
نضرب
الأول في الذي يليه ثم نقسم على2
من 4 الى
20 = 4 في 5 قسمة 2
وعليه
الحد العام ن = ن(ن+1)/ 2
نتأكد
بطريقة الفروق
|
الفرق2 |
|
الفرق1 |
|
مكعبات |
n |
|
|
|
|
|
1 |
1 |
|
|
|
2 |
|
|
1 |
|
|
3 |
2 |
|
|
3 |
|
|
1 |
|
|
6 |
3 |
|
|
4 |
|
|
1 |
|
|
10 |
4 |
|
|
5 |
|
|
1 |
|
|
15 |
5 |
|
|
6 |
|
|
|
|
|
21 |
6 |
الفرق
الثاني ثابت
المعادلة
من الدرجة الثانية
an^2+bn+c
نعوض مرة
n = 1
, 2 , 3
a+b+c
4a+2b+c
9a+3 b+c
16n+4b+c
نحسب الفرق
3a+b
5a+b
7a+b
2a
2a
الفرق
الثابت
2a
2a=1
a=1/2
3a+b=2
b=-1/2
a+b+c =1
c=0
an^2+bn+c
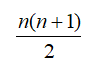
ولإيجاد مجموع المتسلسلة للحد النوني هنالك ثلاث طرق ،
وهي على النحو التالي :
1) من خلال شكل البناء ، على النحو التالي :
وفي هذه الطريقة يتم بناء مجسم مؤلف من ستة نماذج
حتى يكتمل شكل متوازي المستطيلات على النحو التالي :
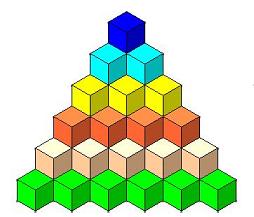

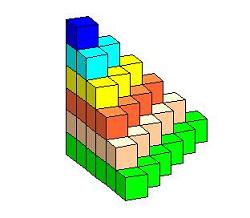 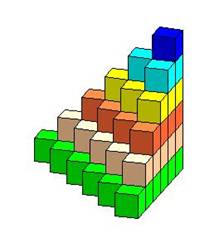
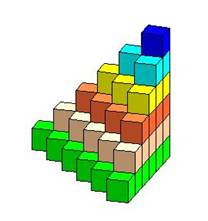 
ومنه نستنج أن مجموع المتسلسلة عبارة عن حجم متوازي
المستطيلات مقسوم على ستة .
2) من خلال الاستنتاج وذلك بإيجاد مجموع عدد من الحدود
وحساب الفرق حتى يثبت الفرق ، كما يلي :
|
الفرق3 |
|
الفرق2 |
|
الفرق1 |
|
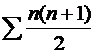 |
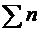 |
n |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
4 |
3 |
2 |
|
1 |
|
|
6 |
|
|
|
4 |
|
|
10 |
6 |
3 |
|
1 |
|
|
10 |
|
|
|
5 |
|
|
20 |
10 |
4 |
|
1 |
|
|
15 |
|
|
|
6 |
|
|
35 |
15 |
5 |
|
|
|
|
21 |
|
|
|
|
|
|
56 |
21 |
6 |
|
|
|
|
|
|
نلاحظ أن الفرق قد ثبت في المرة الثالثة وهذا يبين أن
مجموع المتسلسلة عبارة عن معادلة من الدرجة الثالثة
وهي على الصورة :
 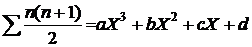
ثم نعوض عن X
بالقيم : 1، 2 ، 3 ، 4 على التوالي ، فينتج لنا
المعادلات التالية :
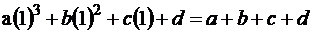 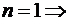
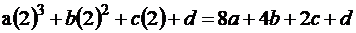 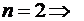
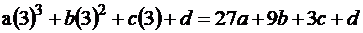 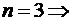
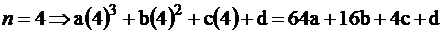
ثم نقوم بحل المعادلات السابقة حتى نحصل على قيم كل
من: (
a b c d
) على التوالي من خلال إيجاد الفرق بين المعادلات
السابقة ،علـــــى النحو التالي :
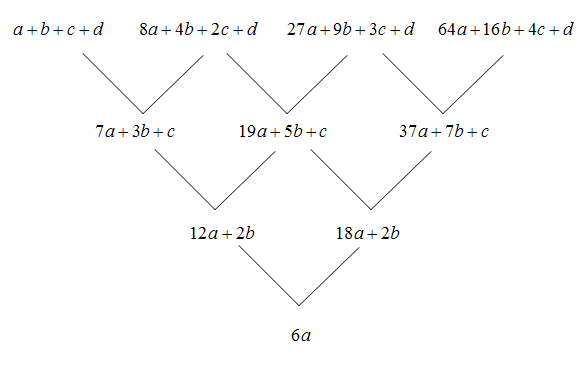
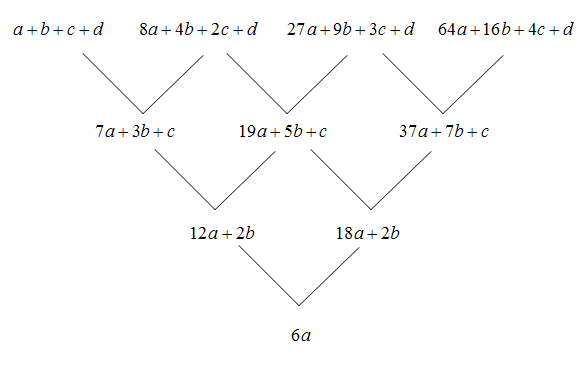
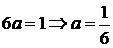
بالتعويض في المعادلة الثانية بقيمة (
a
) :
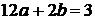
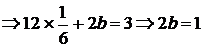
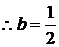
بالتعويض في المعادلة الثانية بقيم (a
،
b
) في المعادلة الثالثة :
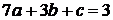
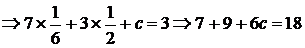
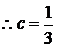
بالتعويض بقيم (
a ،
b ،
c ،
d
) في المعادلة الأساسية ، ينتج :
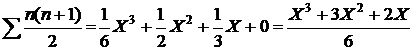
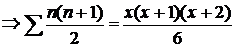
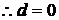
بالتعويض بقيم (
a ،
b ،
c ،
d
) في المعادلة الأساسية ، ينتج :
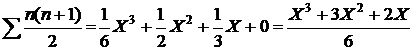
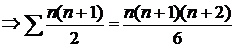
3) من خلال الحساب من القانون بإيجاد مفكوك المجموع ،
على النحو التالي :
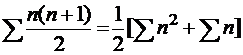
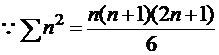
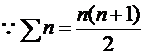
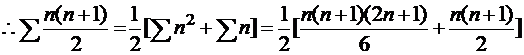
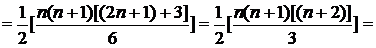
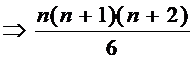
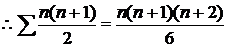
|