متتابعة رقم 16
س4)
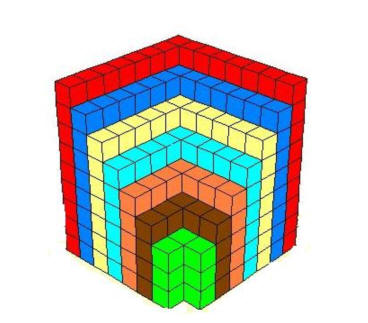
أوجد الحد النوني للمتتابعة الموضحة بالشكل الآتي؟ ثم أوجد المجموع النوني
لهذه المتتابعة؟
الشكل كامل
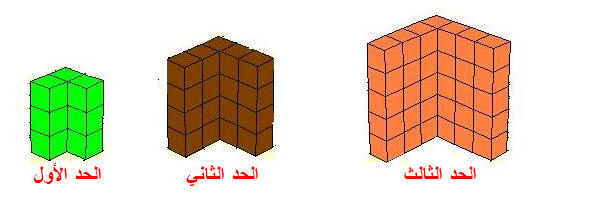
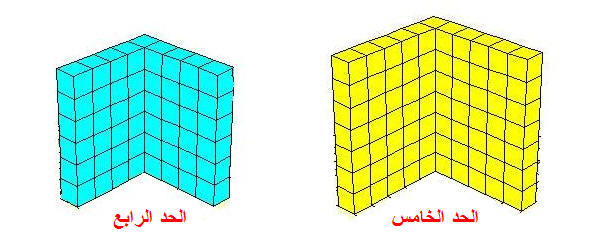
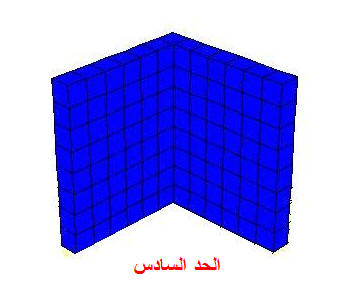
لاحظ الشكل السابق وتتبع تغير عدد المكعبات تبعاً لتغير الحد ،
ثم أجب عن الأسئلة التالية :
1- ما عدد المكعبات الموجودة في
الحد العشرين ؟
2- ما مجموع المتسلسلة لـ ( ن ) حد ؟ وهل يمكن أيجاد قانون
مجموع المتسلسلة بأكثر من طريقة ؟ وضح ذلك ؟
3- ما مجموع عدد المكعبات من الحد الأول إلى الحد الثاني عشر ؟
إجابة السؤال الأول :
كي نستطيع الإجابة على هذا السؤال ينبغي أن نحاول معرفة النمط
الذي تزيد وفقاً له عدد المكعبات مع زيادة رتبة الحد .
حدود هذه المتتابعة ، هي : 9 ، 20 ، 35 ، ......
ولكي نوجد عدد المربعات في الحد العاشر ؛ فلابد أولاً من
إيجاد الحد النوني لها ، ويمكن ذلك من خلال شكل التمثيل
البياني للحدود .
حيث نقوم بمحاولة اكتشاف النمط الذي تسير عليه هذه المتتابعة ،
وهو ما يعني رياضياً إيجاد الحد النوني لها . وعندما نتأمل في
هذه الحدود سنجد أن كل حد منها يتكون عبارة من ارتفاع البناء
مضروب في طول البناء ، وبالتالي يمكن توضيح نمط التغير في
الحدود تبعاً لرتبة الحد ، كما في الجدول التالي :
|
ن |
مج ن |
نمط التغير في الحد |
|
ارتفاع البناء |
أطوال البناء |
|
الجزء الثابت
( ملتقى الطرفين المتغيرين ) |
الجزء المتغير الأول
( أحد أضلاع الزاوية ) |
الجزء المتغير الأول (
أحد أضلاع الزاوية ) |
|
1 |
9 |
3 |
1 |
1 |
1 |
|
2 |
20 |
4 |
1 |
2 |
2 |
|
3 |
35 |
5 |
1 |
3 |
3 |
|
4 |
54 |
6 |
1 |
4 |
4 |
|
5 |
77 |
7 |
1 |
5 |
5 |
|
|
طول´
ارتفاع |
ن+2 |
1 |
ن |
ن |
وبالرجوع إلى الجدول السابق نجد أن :
|
الحد |
|
الفرقالاول |
الفرق
لثاني |
|
1 |
9 |
11 |
4 |
|
2 |
20 |
|
3 |
35 |
15 |
|
4 |
54 |
19 |
4 |
|
5 |
77 |
23 |
4 |
الفرق الثاني ثابت معناه أن المعادلة من الدرجة الثانية
an^2+bn+c
نعوض
مرة n=1 و 2 و3
a+b+c
4a+2b+c
9a+3b+c
16a+4b+c
3a+b
5a+b
7a+b
2a
2a=4
a=2
نعوض
في
3a+b
3a+b =11
b=5
نوجد
قيمة c
a+b+c=9
c=2
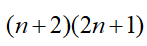
الحد
العام
an^2+bn+c
2n^2+5n+2
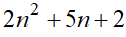
التأكد
n=5
50+25+2=77
طريقة
أخرى
الحد في هذه المتتابعة = ارتفاع الحد ( يساوي دائماً رتبة
الحد مضاف إليها العدد اثنان
´
طول شكل الحد [ ( جزء ثابت ( ويساوي مكعب واحد يقع في زاوية كل
حد ) + جزئين متغيرين في الطول
( كل منها يساوي رتبة الحد )] .
إذاً : ح ن = ( ن
+ 2 ) ´ (
1 + 2 ن )
ح ن =
( ن + 2 ) ´ (
2ن + 1 )
والآن يمكن إيجاد عدد المكعبات في الحد العشرين كما يلي :
ح 20 =
( 20 + 2 ) ´ (
2
´
20 + 1 )
= 22
´
41 = 902 مكعباً .
والآن يمكن إيجاد عدد المربعات في الحد العشرين كما يلي :
ح 10 =
4 × 10 + 2 = 42 مكعباً .
إجابة السؤال الثاني :
ولإيجاد مجموع المتسلسلة للحد النوني هنالك ثلاث طرق ، وهي على
النحو التالي:
1) من خلال الاستنتاج وذلك بإيجاد مجموع عدد من الحدود وحساب
الفرق حتى يثبت الفرق ، كما يلي :
|
الفرق3 |
|
الفرق2 |
|
الفرق1 |
|
 |
 |
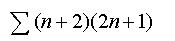n |
|
|
|
|
|
|
|
9 |
9 |
1 |
|
|
|
|
|
20 |
|
|
|
|
15 |
|
|
29 |
20 |
2 |
|
4 |
|
|
35 |
|
|
|
19 |
|
|
64 |
35 |
3 |
|
4 |
|
|
54 |
|
|
|
23 |
|
|
118 |
54 |
4 |
|
|
|
|
77 |
|
|
|
|
|
|
195 |
77 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
نلاحظ أن الفرق قد ثبت في المرة الثالثة وهذا يبين أن مجموع
المتسلسلة عبارة عن معادلة من الدرجة الثالثة وهي على
الصورة:
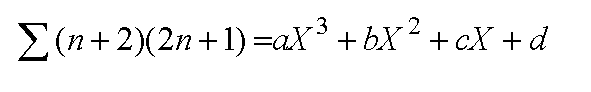
ثم نعوض عن X
بالقيم : 1، 2 ، 3 ، 4 على التوالي ، فينتج لنا المعادلات
التالية :
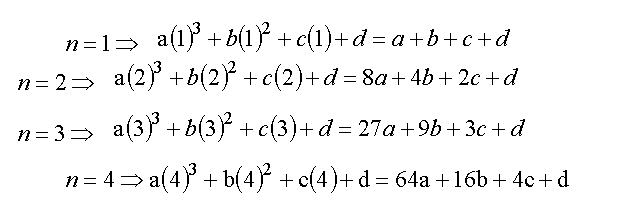
ثم نقوم بحل المعادلات السابقة حتى نحصل على قيم كل من : (
a b c d
) على التوالي من خلال إيجاد الفرق بين المعادلات السابقة
،علـــــى النحو التالي :
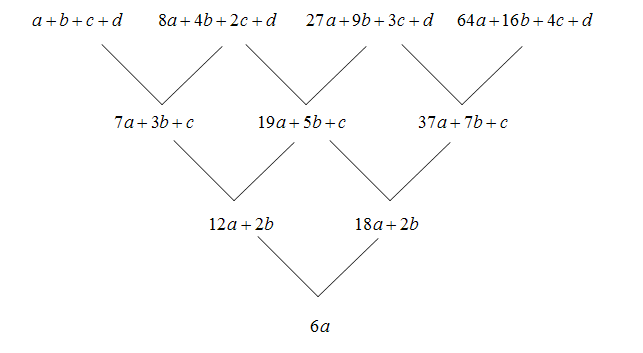
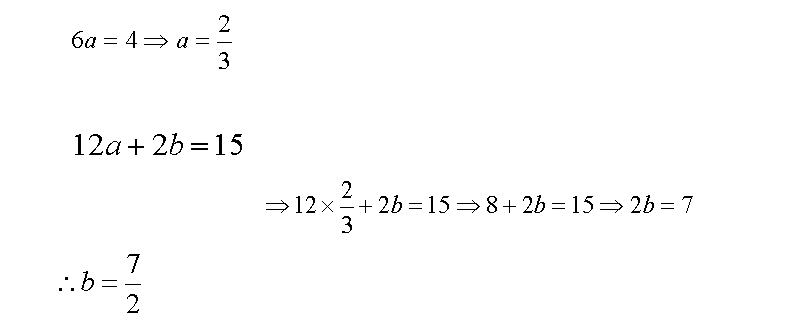
بالتعويض في المعادلة الثانية بقيمة (
a
) :
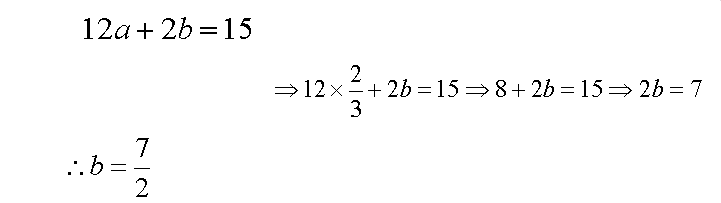
بالتعويض في المعادلة الثانية بقيم (a
، b
) في المعادلة الثالثة
:
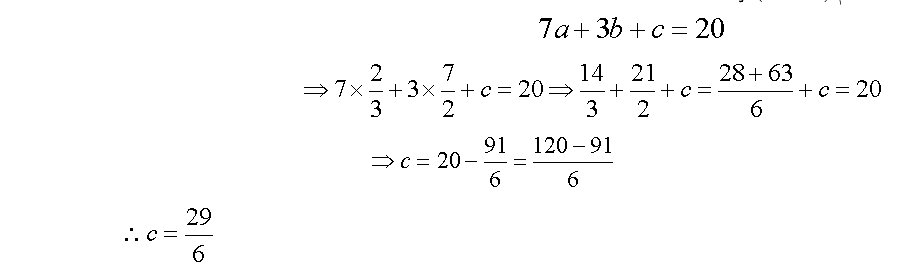
بالتعويض في المعادلة الثانية بقيم (a
، b
، c
) في المعادلة الرابعة :
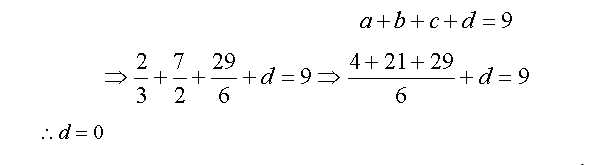
بالتعويض بقيم (
a ،
b ،
c ،
d
) في المعادلة الأساسية ، ينتج :
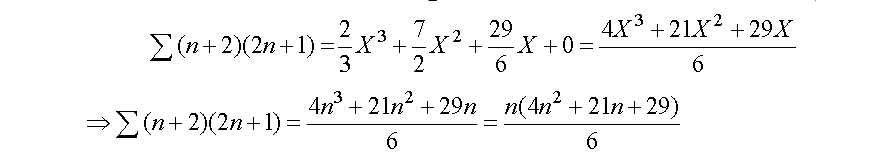
2)
من خلال الحساب من القانون
بإيجاد مفكوك المجموع ، على النحو التالي
:
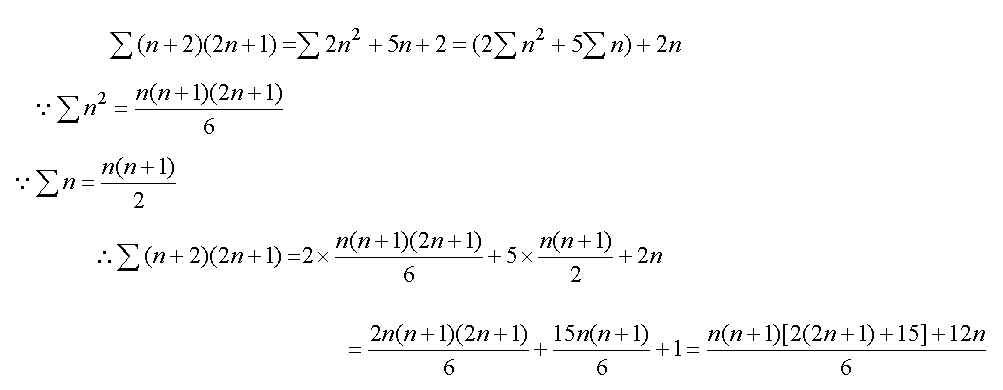
إجابة السؤال الثالث :
مجموع المكعبات إلى الحد الثاني عشر :
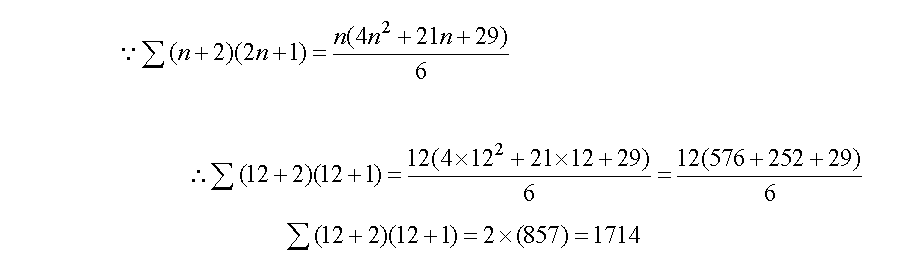
إذا عدد المكعبات المكونة للشكل حتى الحد الثاني عشر = 1714
مكعباً .