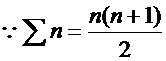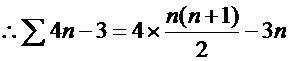متتابعة رقم 15  

 

                                                                                       

 

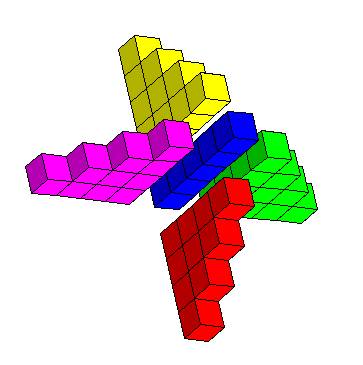
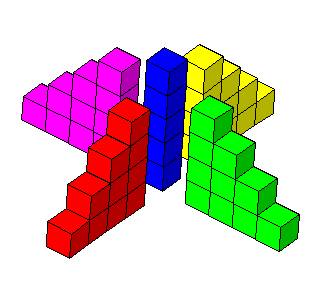
  لاحظ الشكل السابق وتتبع تغير عدد المكعبات تبعاً لتغير الحد ، ثم أجب عن الأسئلة التالية :

1- ما عدد المكعبات الموجودة في الحد الخامس عشر ؟

2- ما مجموع المتسلسلة لـ ( ن ) حد ؟

3- ما مجموع عدد المكعبات من الحد الأول إلى الحد الثاني عشر ؟

 

إجابة السؤال الأول :

كي نستطيع الإجابة على هذا السؤال ينبغي أن نحاول معرفة النمط الذي تزيد وفقاً له عدد المكعبات مع زيادة رتبة الحد .

حدود هذه المتتابعة ، هي : 1 ، 5 ، 9 ، 13  ......

ولإيجاد عدد المربعات في الحد الخامس عشر ؛ فلابد أولاً من إيجاد الحد النوني لها ، ويمكن ذلك بطريقتين :

الطريقة الأولى : من خلال شكل التمثيل البياني للحدود:

ويتم بمحاولة اكتشاف النمط الذي تسير عليه هذه المتتابعة ، وهو ما يعني رياضياً إيجاد الحد النوني لها ، وعندما نتأمل في هذه الحدود سنجد أن كل حد منها يتكون أربعة أجزاء متساوية إضافة إلى جزء أخري يمثل المكعب الذي يقع بين الأجزاء الأربعة وتتصل به هذه الأجزاء من أربعة إتجاهات كما هو واضح في الشكل التالي :

 

 

 

 

 

 

 

  

 

 

 

 

 

 ربما اتضحت الصورة أكثر من خلال الشكل السابق ، ولتتبع تغير الحدود يمكن عمل الجدول التالي :

 

ن

مج ن

نمط التغير في الحد

 

 

الجزء الثابت       ( ملتقى الأجزاء الأربعة )

الجزء المتغير  الأول            

الجزء المتغير  الثاني             

الجزء المتغير  الثالث             

الجزء المتغير  الرابع

 

1

1

1

0

0

0

0

 

2

5

1

1

1

1

1

 

3

9

1

2

2

2

2

 

4

13

1

3

3

3

3

 

5

17

1

4

4

4

4

 

 

 

1

ن-1

ن-1

ن-1

ن-1

 

 

 

وبملاحظة الجدول ، نجد أن :

 الحد في هذه المتتابعة = مجوع الأجزاء الأربعة المتغيرة ( كل حد يساوي رتبة الحد مطروح منه العدد واحد ) مضاف إليها الجزء الثابت ( يساوي الواحد الصحيح ) .

  إذاً : ح ن =  4  ´ ( ن-1 ) +  1  

ح ن  =   4ن     -      4      +        1

ح ن  =   4ن     -    3 

 

 

الطريقة الثانية : باستخدام القانون العام لإيجاد الحد النوني للمتتابعة الحسابية :

يمكن ملاحظة أن المتتابعة السابعة متتابعة حسابية حيث أنها تزيد بمقدار ثابت لذلك يمكن استنتاج الحد النوني ، من خلال القانون العام لإيجاد الحد النوني للمتتابعات الحسابية ، كما يلي :

 ح ن = أ + ( ن - 1 ) د

حيث : أ هو الحد الأول ، د هو أساس هذه المتتابعة

أ = 1 ، د = 4

ح ن = 1 + 4 ( ن - 1 )

= 1 + 4ن - 4

ح ن = 4ن - 3

والآن يمكن إيجاد عدد المكعبات في الحد الخامس عشر كما يلي :

ح 20 =  4 ´ 15  -    3

= 60  - 3 =  57  مكعباً .

 

 إجابة السؤال الثاني :

ولإيجاد مجموع المتسلسلة للحد النوني هنالك طريقتين، وهي على النحو التالي:

 

1) من خلال الاستنتاج وذلك بإيجاد مجموع عدد من الحدود وحساب الفرق حتى يثبت الفرق ، كما يلي :

 

 

الفرق2

 

الفرق1

 

n

 

 

 

 

1

1

1

 

 

5

 

4

 

 

6

5

2

 

9

 

4

 

 

15

9

3

 

13

 

4

 

 

28

13

4

 

17

 

 

 

 

45

17

5

 

 

 

 

 

 

 

 

6

 

 

 

 

نلاحظ أن الفرق قد ثبت في المرة الثانية وهذا يبين أن مجموع المتسلسلة عبارة عن معادلة من الدرجة الثانية وهي على الصورة:

                                                                                                                                                

                                                                                                          

إذا :

                                                                                            

ثم نعوض عن  n     بالقيم : 1، 2 ، 3  على التوالي ، فينتج لنا المعادلات التالية :

Put : n=1,2,3

      

      

      

 

 

ـــــ

ـــــ

 

 

 

 

 

 

 

 

ـــــ

 

 

 

 

 

 

 

 

 

      

 

 

 

 

 

 

 

 

 

 

 

 

ثم نقوم بحل المعادلات السابقة حتى نحصل على قيم كل من : (   a  b  c  d   ) على التوالي  من خلال إيجاد الفرق بين المعادلات السابقة ،علـــــى النحو التالي :

                                                                                                                                          

بالتعويض في المعادلة الثانية بقيمة ( a ) :

                                                                                                                                                  

                                                                                                                 

                                                                                                                                                      

بالتعويض بقيم (a  ، b ) في المعادلة الثالثة :                                                   

                                                                                                                                              

             

بالتعويض بقيم (a  ، b ، c ) في معادلة مجمع المتسلسلة (المعادلة الأساسية ) ، ينتج :

                                                                                                                       

                                                                                                                        

 

2) من خلال الحساب من القانون بإيجاد مفكوك المجموع ، على النحو التالي :

                                                                                                                     

‍                                                                                                                                 

                                                                                                         

                                                          

                                                                                                                       

 

 

إجابة السؤال الثالث :

 يمكن إيجاد مجموع حدود المتسلسلة  ( عدد المكعبات ) إلى الحد الثاني عشر من خلال استخدام قانون حساب مجموع الحد النوني للمتسلسلة ، على النحو التالي:

 

                                                                                                                   

                                                                                     

                                  

إذا عدد المكعبات المكونة للشكل حتى الحد الثاني عشر = 276 مكعباً .