متتابعة رقم 14

 مثال : ليكن لدينا الشكل التالي:   

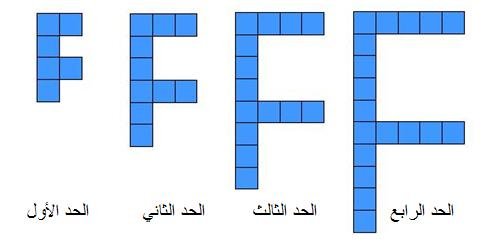
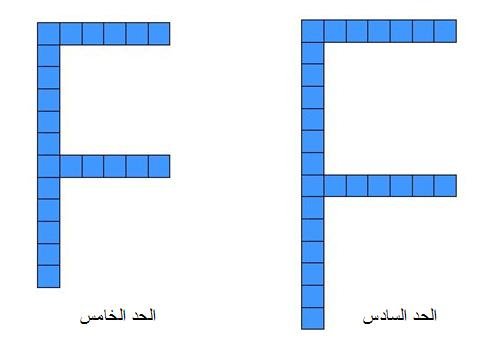
والسؤال : أوجد عدد المربعات في الحد العاشر ؟

الحل :

حدود هذه المتتابعة الأولى ، هي : 6 ، 10 ، 14 ، ......

ومن الواضح أنها متتابعة حسابية ، حدها الأول = 6 ، وأساسها = 4 .

ولكي نوجد عدد المربعات في الحد العاشر ؛ فلابد أولاً من إيجاد الحد النوني لها ، ويمكن ذلك بأكثر من طريقة :

الطريقة الأولى : من خلال شكل التمثيل البياني للحدود:

ويتم بمحاولة اكتشاف النمط الذي تسير عليه هذه المتتابعة ، وهو ما يعني رياضياً إيجاد الحد النوني لها ، وعندما نتأمل في هذه الحدود سنجد أن كل حد منها يتكون من :

وهذه الأجزاء يمكن توضيح الثابت والمتغير منها كما في النموذج التالي :

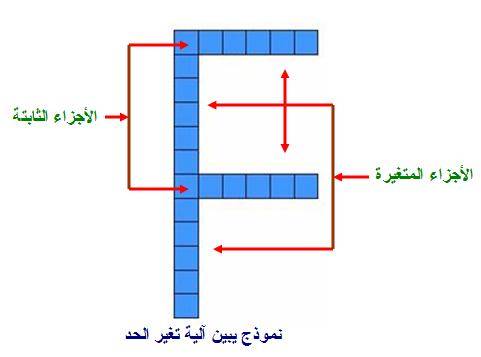
وبالرجوع إلى الجدول السابق نجد أن :

 الحد في هذه المتتابعة = جزئين ثابتين ( كل منهما مكون من مربع واحد )

                                                    + أربعة أجزاء متغيره بتغير الحد ( كل منها يساوي رتبة الحد ) .

  إذاً : ح _ن =            2               +     4 ن

ح _ن  =   4 ن   +    2

ح _ن  =  2( 2 ن   +  1 )

والآن يمكن إيجاد عدد المربعات في الحد العاشر كما يلي :

ح ₁₀ = 2( 2 × 10 + 1 ) = 42 مربعاً .

الطريقة الثانية : باستخدام القانون العام  للحد النوني للمتتابعة الحسابية :

 ح _ن = أ + ( ن - 1 ) د

حيث : أ هو الحد الأول ، د هو أساس هذه المتتابعة

أ = 6 ، د = 4

ح _ن = 6 + 4 ( ن - 1 )

= 6 + 4ن - 4

ح _ن = 4ن + 2

والآن يمكن إيجاد عدد المربعات في الحد العاشر كما يلي :

ح ₁₀ = 4 × 10 + 2 = 42 مربعاً