تعلم التفكير
|
|
تعلم التفكير |
|
يدوية وبرمجية
البرمجية على الرابط
صممت هذه البرمجية لتخدم تعلم الرياضيات للطلاب بصفة عامة
وقد تم تصميمها بمكعبات بلاستيكية ليحسها الكفيف وضعاف البصر بصفة خاصة
الفردية
وهذه بعض استخداماتها
- التصنيف :
- الأنماط
المقارنة
- مفهوم العدد
-العدد السابق-العدد التالي
- مكونات العشرة
-الجمع بدون حمل- الجمع مع الحمل
- الجمع بالاكمال الى العشرة
-الطرح بدون استلاف- الطرح بالاستلاف
- الضرب
- توزيع الضرب على الجمع
- القسمة بدون باقي
- القسمة مع الباقي
العدد الفردي
العدد الزوجي
-مجموع عددين فرديين
-مجموع عددين زوجين
-مجموع عدد فردي وعدد زوجي
-مجموع الأعدادالزوجية
-مجموع الأعداد الفردية- مجموع الأعداد المتتالية
- علاقة التعدي
- المربع
- المستطيل
- المساحة
- المحيط
-التناظر. الانسحاب الدوران
-النسبة- تشابه المضلعات
-تمثيل البيانات بأعمدة- قواسم العدد
- القاسم المشترك الأكبر لعددين
- المضاعف المشترك الأصغرلعددين
- الكسور
المكعب
الموشور
الحجم
التصنيف :
يتم اعطاء الطالب المجموعة كاملة ويطلب منه تصنيفها
أحد التصنيفات
الأعداد الفردية
الأعداد الفردية بالمكعبات ( الألوان مختلفة )
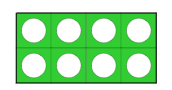
الأعداد الزوجية ( الألوان مختلفة )
الأعداد الزوجية بالمكعبات
برمجية رسم المجسمات
https://www.nctm.org/Classroom-Resources/Illuminations/Interactives/Isometric-Drawing-Tool/
الأعداد المتتالية بمكعبات الوحدة
هل لااحظت أن مجموع الأعداد المتتالية = نصف مجموع الأعداد الزوجية
حيث نرى نمط معين تسير عليه القطع
الأنماط :
الحد العام الحد الرابع الحد الثالث الحد الثاني الحد الأول
ارسم الشكل العاشر واحسب عدد الدوائر في ذللك الحد
الحد العام الحد الرابع الحد الثالث الحد الثاني الحد الأول
ما القانون العام الذي يمكن به معرفة أي حد ؟ العاشر مثلا
ما القانون العام الذي نعرف به مجموع الدوائر في عدد محدد من الحدود؟ الجدود العشرة الأولى مثلا
المقارنة:
يتم اعطاء الطالب قطعتين ويقارن بينهما من حيث عدد الدوائر التي يتكون منها كل شكل ( اكبر من او أصغر من أو يساوي )
عشرة أكبر من 9
تمثيل وكتابة الأعداد حتى عشرة ومعرفة العدد والعدد االذي قبله والعدد الذي بعده
1
2
3
4
5
6
7
8
9
10
واحد اثنان ثلاثة أريعة خمسة ستة سبعة ثمانية تسعة عشرة
مكونات العشرة
و
و
و
و
و
الابدال في الجمع
+
+
+
+
+
1
9
2
8
3
7
4
6
5
5
+
+
+
+
+ 9
1
8
+
2
7
3
6
4
5
5
من مكونات العشرة نلااحظ أنه من معرفة أحد مكونات العشرة ممكن أن نعرف العدد الآخر وذلك بطرح ذلك العدد من العشرة
ملاحظة :
في عملية الجمع 4+6= 10 نلاحظ أن
10-6=4
وأن
10-4=6
10-*=6 يكون * =4 وذلك بطرح 6 من 10
الجمع:
يمكن تدريس مفهوم الجمع باختيار اي قطعتين ومعرفة الناتج بمطابقة المجموع بقطعة ثالثة
لجمع: 3+5
لجمع 4+6
نشاط : احسب الحد المفقود
14+* = 20
+ * =
من الممكن الاستفادة من درس مكونات العشرة بحذف 10 من الطرفين يبقى
+ * =
وبطرح 4 من 10 يكون الناتج 6
وعليه يكون الناتج
4+6=10
الجمع بالاكمال الى العشرة :
بعد ان درس الطالب مكونات العشرة يجب توظيف ذلك في عملية الجمع مثل جمع 9 +7
نضعهما جوار بعضهما
نختبر الناتج بالقطقة ذات العشر مربعات كما في الشكل التالي
فيكون الناتج 10 و 6 = 16
طريقة أخرى :
يتم تقسيم 7 الى عددين احدهما يكمل العدد الأول الى 10
=
حتى نكمل 10 ويكون الناتج 16
لجمع 8 +7 نقسم 7 الى عددين احدهما يكمل العدد الاول الى العشرة 2+5
اجمع 34+25
آحاد عشرات اجمع 34+29
آحاد عشرات
يتم استبدالهما
3 60
الطرح :
ناقص
9- 6 = 3
مثال
17- 8 =؟
ناقص
نضع الثمانية من بداية المطروح منه وكأننا نطرح 8 من العشرة فيبقى 2 نجمعها مع المطروح = 9
نطرح الثمانية من 10 فيبقى 2 تضاف الى المطروح فيكون الناتج 9
نشاط : 28- * = 15
لحل مثل هذه الحالات لابد من أن يفهم الطالب
أنه لوكان لديه أي مبلغ وصرفه كله لا يبقى معه شيء
28- 28= 0
ولو كان معه أي مبلغ ولم يصرف منه شيء يبقى المبلغ كما هو
28- 0= 28
28- *= 15
نجعل المبلغ صفرا
لمعرفة* نطرح 15 من 28
وعليه
- * =
بعد حذف 10 من الطرفين يبقى
- * =
لمعرفة * نطرح 5
الضرب :
يتم تمثيل الضرب وفق المجموعات والعناصر في كل مجموعة فالعدد الأول يمثل عدد المجموعات والعدد الثاني يمثل عدد العناصر في كل
مجموع
ضرب 5 في 4 يعني 5 مجموعات وكل مجموعة فيها 4عناصر
بينما 4 ضرب 5 تمثيله 4 مجموعات وفي كل مجموعة 5 عناصر
أربعة في خمسة خمسة في أربعة
توزيع الضرب على الجمع
أx ب +أ x ج = أ ( ب+ج )
2 في 3 + 2 في 2 = 2 في 5
=
القسمة :
بمفهوم المجموعات والعنصر
12 قسمة 4 تعني 12 فيها كم 4
12
مجموعة1 مجموعة 2 مجموعة 3 بينما
12 قسمة 3 يعني
12 فيها كم 3
12
مجموعة1 مجموعة 2 مجموعة 3 مجموعة 4 ويمكن تمثلها بتمثيل 12 بالقطع ونرى كم 3 في 12
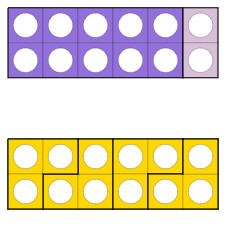
12 تقسيم 3 يساوي 4
وتعني 12 فيها كم 4
لقسمة 12 على 4 نمثلها بالطريقة نفسها
وكم 4 في 12
وبالطريقة نفسها يمكن تمثيل القسمة بباقي فمثلا 14 تقسيم 3 نكون مجموعات من 3 ونبحث كم عدد المجموعات ؟ وكم الباقي ؟
مجموعة1
مجموعة 2
مجموعة3
مجموعة4
الباقي
أما 14 تقسيم 4 تعني لدينا 14 ونريد توزيعها أربعات فكم 4؟ وكم الباقي؟
مجموعة1
مجموعة 2
مجموعة3
الباقي
وهذا يحقق قانون القسمة الاقليدية
المقسوم =( المقسوم عليه في خارج القسمة ) + الباقي
تمثيل الأعداد الكبيرة :
كتابة العدد 2782
احاد عشرات مئات الوف
3
80
700
2000
جمع 37 +45
آحاد عشرات
نجمع الآحاد فنجد أن المجموع :
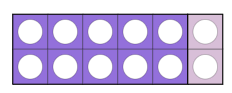
12
نجمع العشرات ونضيف لها هذه العشرة فيكون الناتج
2
8
بالطريقة نفسه تتم عملية الطرح
قسمة الأعداد الكبيرة:
مثال : 54 قسمة 3
بتقسيم 5 على 3 يكون
نمثل أول عدد من المقسوم من ناحية اليسار
بتقسيم 5 على 3 يكون الناتج واحد والباقي 2
نبحث عن عدد المرات التي يمثلها المقسوم عليه
الناتج واحد والباقي 2 ( عشرين )
نمثل العدد 24
نختبر 24 فيها كم 3
24 فيها كم 3 الناتج 8
ناتج القسمة = 18
636 تقسيم 4
9 5 1
6 3 6 المقسوم عليه
36 36
---
0
23 20
---
3
6
4
---
2
4
بالطريقة نفسها يمكن قسمة 976 على 8
6
7
9
الأعداد الفردية:
1
3
5
7
9
الأول الثاني الثالث الرابع الخامس السادس السابع العاشر
لاحظ ان هذه الأعداد مكونة من صفين غيركاملين
الصيغة العامة هي 2ن - 1
فردي+ فردي
زوجي + فردي
زوجي+ زوجي
مجموع الاعداد فردية :
1
3
مربع 2 في 2
1
3
5
مربع 3 في 3
عدد الحدود = 3
1
3
5
4
مربع 4 في 4
عدد الحدود =4
عدد الحدود 5 المجكوع مربع 5 في 5
عدد الحدود ن المجموع ن في ن = ن تربيع
الأعداد الزوجية:
2
4
6
8
الأول الثاني الثالث الرابع الخامس السادس السابع العاشر لاحظ ان هذا النوع من الأعداد مكونة من صفين كاملين
الصيغة العامة هي 2 ن
مجموع الاعداد الزوجية:
الحد الأول
الحد الثاني
المجموع
2
4
مستطيل 2 في 3
عدد الحدود = 2
الأول
الثاني
الثالث
المجموع
2
4
6
مستطيل 3 في 4
الأول
الثاني
الثالث
الرابع
المجموع
2
4
6
8
مستطيل 4 في 5
مجموع ن حد من الأعداد الزوجية= ن ( ن+ 1)
مجموع الأعداد المتتالية :
الأول
الثاني
الثالث
الرابع
المجموع
2
4
6
8
مستطيل 4 في 5
الأعداد المتتالية = نصف الأعداد الزوجية
الأول 2
الثاني 4
الثالث 6
الرابع 8
المجموع
نصف مستطيل 4في5
مجموع ن حد من الأعداد المتتالية= نصف ن ( ن+1)
علاقة التعدي :
اذا كان أ أكبر من ب
ب أكبر من ج
فان أ أكبر من ج
أ
ب
ج
قواسم العدد:
قواسم العدد هي مجموعة الأعداد التي تقبل القسمة على ذلك العدد . ومعروف أن أي عدد يقبل القسمة على نفسه وعلى الواحد.
قواسم العدد 24 =1و24
24
1
24 2
12 3
8 4
6 من الممكن استخدام هذه الوسيلة لمعرقة قواسم 24غير الواحد والعدد نفسه
1
24 2
12 3
8 4
6 الهدف هو تعريف الطالب بمفهوم قواسم العدد ومعناه وليس ارهاقه في حساب قواسم أعداد كبيرة لوجود العديد من البرمجيات التي تحسب قواسم أي عدد
وهذا رابط أحدها
https://aghandoura.com/NF/1/FACTORS.html
مضاعفات العدد : هي مجموعة الأعداد التي تقبل القسمة على ذلك العدد
مثال العدد ثلاثة : مضاعفاته 6 و 9 و 12 و15و 18و 21 و 24 ............
العدد أربعة : مضاعفاته 8 و12و 16 و20 و24 و.............
المضاعف المشترك الأصعر للعددين 6 و 8 هو 24
المساحة:
عدد الوحدات المربعة داخل المضلع
المحيط:
مجموع أطوال المضلع
المساحة المساحة المساحة المحيط المحيط المحيط
نشاط : احسب محيط ومساحة كل شكل
المساحة المساحة المساحة المساحة المساحة المساحة المساحة المساحة المساحة المساحة
المحيط المحيط المحيط المحيط المحيط المحيط
المحيط
المحيط
المحيط
المحيط
المربع : شكل رباعي زواياه قوائم وأضلاعه متتطابقة
المساحة=4 المساحة=9 المساحة 16 المحيط =8 المحيط=12 المحيط =16 نشاط : قارن بين محيط كل شكل
المستطيل : شكل رباعي زواياه قوائم وكل ضلعين متقابلين متطابقين
مستطيل 1
مستطيل 2
التحويلات الهندسية :
التناظر حول المحور الصادي
التناظر حول المحور السيني :
الدوران 90 درجة مع عقارب الساعة :
الشكل الأساس
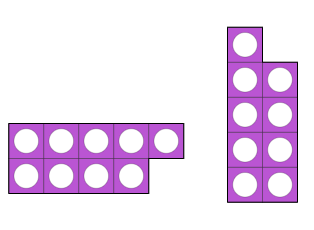
الدوران 90 درجة عكس عقارب الساعة :
الشكل الأساس
الانسحاب نحو اليمين وحدتين :
الشكل الأساس
النسبة : النسبة بين عدد المربعات الموجودة في الصف العلوي الى عدد المربعات الموجودة في الصف السفلي
4:3
4:2 5:4
المجموعةالأولى المجموعة الثانية النسبة
الأولى : الثانية
7
9 9:7
تمثيل البيانات بأعمدة:
الكسور : الهدف من تعلم العمليات على الكسور هو أن يفهم الطالب كيفية تمثيل الكسور والعميات عليها
وليس ارهاقه في حساب عمليات عليها فهناك العديد من التطبيقات والآت الحاسبة عن الكسور
https://www.calculatorsoup.com/calculators/math/fractions.php
تمثيل الكسور
البسط
المقام
الكسر القيمة نصف ثلث 3 أرباع سبعة من 9 ربع جمع الكسور المتحدة المقامات :
الطريقة :
أولاً: نقوم باختيار الشكل الذي يمثل مقام أحدالكسرين وهذا الشكل الناتج يمثل الوحدة ( الواحد الصحيح )
ثانياً: نمثل الكسر الأول .
ثالثاً: نمثل الكسر الثاني
اجمع
الوحدة الكسر الأول الكسر الثاني الناتج
+
ثلاثة أخماس
وفي حال كون الناتج أكبر من الوحدة نكون وحدة ثانية مثل جمع ثلاثة أخماس + 4 أخماس
الوحدة الكسر الأول الكسر الثاني الناتج
+
ثلاثة أخماس
4 أخماس
خمسين
واحد صحيح
=================================================================================
جمع الكسور المختلف المقامات الفيديو
الطريقة :
أولاً: نقوم باختيار الشكل الذي يمثل مقام الكسر الأول ونكرر الشكل بعدد مرات مقام الكسر الثاني وهذا الشكل الناتج يمثل الوحدة ( الواحد الصحيح )
ثانياً: نمثل الكسر الأول .
ثالثاً: نقوم باختيار الشكل الذي يمثل مقام الكسر االثاني ونكرر الشكل بعدد مرات مقام الكسر الأول وهذا الشكل الناتج يمثل الوحدة ( الواحد الصحيح )
رابعا : نمثل الكسر الثاني .
خامسا نجمع تمثيل الكسرين على الوحدة
ملاحظة :- في حال احتاج الناتج إلى تبسيط نقوم بعملية التبسيط
- في حال كان المجموع أكثر من الوحدة نكون وحدة ثانية
الحالة الأولى :
ناتج الجمع أقل من الواحد الصحيح
مثال اجمع ثلث + ربع
مقام الأول 3 ومقام الثاني 4
الوحدة
الوحدة + الكسر الأول اكسر الثاني = الناتج سبعة من 12 ثلث= 4مربعات
ربع= 3 مربعات
وفي حال كون ناتج الجمع أكبر من الواحد الصحيح نكون وحدة ثانية مثل جمع نصف + ثلثين
الوحدة1 الوحدة2 الكسر الأول الكسر الثاني الناتج
+
3 مربعات
4 مربعات
سدس
واحد
اجمع
الوحدة الوحدة
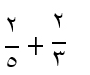
الكسر الأول الكسر الثاني
ثلثين = 10مربعات
خمسين = 6 مربعات
الناتج
واحد من 15
واحد صحيح
سبق دراسة جمع كسرين بطريقة بناء مستطيلين متطابقين نمثل على احدهما الكسر الأول ونمثل الكسر الثاني على المسنطيل الثاني
لجمع ثلثين وخمس
نبني مستطيل بعده الأول مقام الكسر الأول والبعد الثاني مقام الكسر الثاني ونمثل عليه أفقيا الكسر الأول
ومستطيل آخر ونمثل عليه عموديا الكسر الثاني
نجمع تمثيل الكسرين في مستطيل ثالث وفي حال كان الناتج أكثر من الواحد نبني مستطيل اضافي
المجموع الخمس
الثلثين
المجموع
الكسر الثاني الكسر الأول
الحالة الثانية :
مقام أحد الكسرين مضاعف لمقام الكسر الآخر
1- من الممكن حلها بالطريقة الأولى ببناء وحدتين
2- الاكتفاء ببناء وحد واحدة
مثال سدس + ثلث
الحل بالطريقة الأولى ( تكوين وحدتين )
الوحدة الوحدة2 + الكسر الأول اكسر الثاني 
سدس= 3مربعات
ثلث= 6 مربعات
الناتج تسع مربعات من 18 هل لاحظت أن الوحدة2 مكونة من ستة أشكال مجموعها 18 مربع نصف الوحدة = 9 مربعات
وعليه يكون ناتج الجمع = نصف
الحل بالطريقة الثانية ( تكوين وحدة واحدة )
اجمع
سدس + ثلث
نبني الوحدة بمستطيل عدد مربعاته = العدد الأكبر في المقامين ( ستة في هذه الحالة ) وأحد بعدي المستطيل العدد الذي في المقام الثاني كما في الشكل أدناه
الوحدة سدس الوحد= واحد مربع ثلث الوحدة 3 مربعات
نلااحظ أنه يمكن بناء الكسرين من هذه الوحدة دون الحاجة لبناء وحدة ثانية ..
الوحدة الكسر الأول + الكسر الثاني المجموع سدس= 1مربع
ثلث= 2 مربع
ثلاثة أسداس نصف
الطريقة الثانية:
في حال عدم امكانية تحقق ذلك يتم بناءالوحدة من المربعات الصغيرة
مثال ربع + 5 من 12 لا يمكن بناء مستطيل من 12وأحد بعديه 4 في مثل هذه الحالة نبني المستطيل من المربعات الصغيرة التي يمثل الواحد منها الوحدة على ان يكون احد بعدي المستطيل العدد الذي في مقام الثاني
في هذه الحالة يكون بعدي المستطيل 4 و 3 وليس 2 و 6 مثلا
حيث كل مربع يمثل جزء من 12 مع امكانية تمثيل الربع
الحالةالثالثة:
وجود قاسم مشترك بين الكسري مثل سدس + ثمن فبدلا من بناء الوحدة من حاصل ضرب المقامين 6 في 8
نحسب المضاعف المشترك الأصغر للعددين
الطريقة المعتادة نحسب مضاعفات كل منهما ونلاحظ اول مضاعف مشترك بينهما
32 24 16 8 24 18 12 6 وأسهل طريقة لحسابه نضاعف العدد الأكبر الموجود في أحد المقامين حتى نجد عدد يقبل القسمة على العدد الأصغر ففي المثال السابق العدد الأكبر هو 8 اذا
ضاعفناه يصبح 16 ولكن 16 لا يقبل القسمة على 6 نبحث عن المضاعف الذي يليه وهو 24 الذي يقبل القسمة على 6 ويكون هو الوحدة
الطريقة : الوحدة مكونة من 24 مربع يمكن بها تمثيل مقام الكسر الأول( سدس ) بالقسمة على 4وتمثيل مقام الكسر الثاني (ثمن ) بالقسمة عل 3
مقام الأول 6 مقام الثاني
الوحدة 24
الوحدة
الوحدة
الكسر الأول + الكسر الثاني سدس=4 مربعات ثمن=3 مربعات
الناتج سبعة من 24
في حال كون المقامين كبيرين مثل 24 و36 أو غير ذلل يمكن حساب المضاغف المشترك الأصغر بين المقامين بطريقة التحليل
الأول الثاني القاسم المشترك 24 36 2 12 18 2 6 9 3 2 3 نستمر في التحليل حتى لا يكون بين العددين قاسم مشترك ولكي نحصل على القاسم المشترك الأكبر للعديين نضرب الأعداد الناتجة
في العمود ( 2 في 2 في 3 = 12)
ولحساب المضاعف المشترك الأصغر للعدين نضرب الناتج في الأعداد الأفقية
المضاعف المشترك الأصغر للعددين = 2 في 2في 3 في 3 في 2 = 72
القاسم المشترك الأكبر للعددين 24 و 36 = 2 في 2 في 3 في 3 في 2 = 72 ويمكن حساب المضاعف المشترك الأصغر لعددين من معرفة قاسمهما المشترك الأكبر
وذلك بضرب العددين وقسمة النلتج على المقاسم المشترك الأكبر لهما
المضاعف المشترك الأصغر = ( حاصل ضرب العددين) مقسوما على القاسم المشترك الأكبر لهما
وليس الهدف هو ارهاق الطالب في حساب المضاعف المشترك الأصغر للأعاد الكبيرة فهناك العديد من البرامج التي تحسب ذلك مثل الذي على الرابط التالي :
https://www.aghandoura.com/SOLVING/GETHAMY/APPLET/-LCM-of-Two-Numbers.html
طرح الكسور:
الكسور المتشابهة
طرح كسرين مختلفين
طرح كسر من عدد صحيح
طرح كسر من عدد كسري
طرح عدد كسري من عدد صحيح
طرح كسر من كسر غير حقيقي مقام احدهما مضاعف للاخر
ضرب عدد صحيح في كسر
2 في 2 وثلث
سبق أن درسنا 3 في 2 واعتبرنا العدد الأول هو عدد المجموعات والعدد الثاني عدد العناصر في المجموعة
في هذا المثال 2 مجموعات وفي كل مجموعة 2 وثلث
اذا اعتبرنا القطعة المكونة من 3 مربعات هي الوحدة فان الثلث مربع واحد
الوحدة الثلث 2 وثلث مرتين الناتج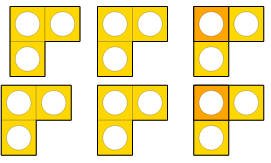 
ثلثين 4 ضرب كسر في عدد صحيح ربع في 5
المعنى ربع الخمسة
التمثيل نختار قطعة تمثل الكسر ( ذات الأربع دوائر) نكررها بعدد مرات العدد الصحيح
الوحدة الربع ربع الخمسة الناتج ربع واحد
طرح عددين كسريين
وهناك العدد من التطبيقات التي تجري العمليات الحسابية على الأعداد الكسرية مثل :
https://www.calculatorsoup.com/calculators/math/mixednumbers.php
ضرب عددين كسريين :
ضرب عددين كسريين : تكمن الفكرة في تمثيل الوحدة بمستطيل بعده الأول مقام الكسر الأول وبعده الثاني مقام الكسر الثاني والاستفادة
من قانون توزيع الضرب على الجمع حيث نكتب العدد الأول كما هو والعدد الثاني نكتبه على صورة عدد صحيح + كسر
2 ونصف في 2 وثلث = 2ونصف ( 2 + نصف )الوحدة في هذا المثال
النصف
تمثيل العدد الأول
2ونصف حاص الضرب وفق توزيع الضرب على الجمع
اثنين ونصف( 2+ ثلث)
2 ( اثنين ونصف)
ثلث (اثنين ونصف )
+ خمسة
خمسة أسداس
المجموع
خمسة خمسة أسداس خمسة وخمسةأسداس +
=
الهدف هو تمثيل العملية وليس الحل بهذه الريقة والس الهدف ارهاق الطالب بتمارين ذات أعداد كبيرة فهناك العديد من الات الحاسبة التي تجري العمليات على الكسور بصفة عامة
وضرب عددين كسريين بصفة خاصة
الرابط التالي لأحدى هذه الآات
طريقة المربعات: ضرب واحد وثلث في 2 ونصف
العدد الكسري الثاني يكتب في صورة ( كسر + عدد صحيح )
باستخدام قانون توزيع الضرب على الجمع
واحد وثلث ضرب اثنين ونصف نكتبها بالطريقة التالية :
واحد وثلث ( نصف + 2 )= نصف (واحد وثلث )+ 2( واحد وثلث )
التشابه : هو التكبير بنسبة محددة
لاحظ التكبير وقارن بين النسبة بين الأضلاع والنسبة بين المساحات
النسبة 1
2
بين الأضلاع 1
4
بين المساحتين
النسبة 1
3
بين الأضلاع 1
9
بين المساحتين
النسبة 1
4
بين الأضلاع 1
16
بين المساحتين
تكبير المستطيل
النسبة 1
2
بين الأضلاع 1
4
بين المساحتين
النسبة بين أضلااع المستطيل الصغير :أضلآع المستطيل الكبير هي 1: 2
من حيث الأضلاع النسبة 2:1
من حيث الكبر المستطيل الكبير كم مرة قد الصغير؟
اذا اعتبرنا المستطيل الصغير هو الوحدة من حيث المساحة فان المستطيل الكبير قد الصغير 4 مرات
النسبة بين الأضلاع 1 : 3
النسبة 1
3
بين الأضلاع 1
9
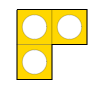
بين المساحتين المتتاليات وحساب الحد النوني
ارسم الحد العاشر
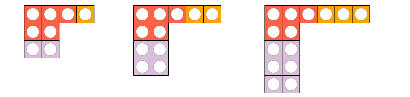
احسب كم نقطة في الحد العاشر
اوجد القانون الذي يحدد عدد النقاط في حد بعينه
احسب مجموع النقاط في العشر حدود الأولى
ما القاعدة التي بها يمكنأن يحدد عدد النقاط في عدد محدد من الحدود
النسبة بين أضلااع المستطيل الصغير : أضلآع المستطيل الكبير هي 1: 3
المستطيل الكبير كم مرة قد المستطيل الصغير؟
اذا اعتبرنا المستطيل الصغير هو الوحدة من حيث المساحة فان المستطيل الكبير قد الصغير 9 مرات
هل لاحظت العلاقة بين النسبة بين الأضلاع والنسبة بين الشكلين في الكبر ( المساحة )
النسبة بين مساحتي شكلين متشابهين = مربع نسبة التشابه
المكعب
متوازي المستطيلاات ( الموشور )
الحجم: عدد المكعبات في المجسم يمكن حسابه من معرفة عدد المكعبات في الدور مضروبا في عدد الأدوار
