الكسور الاعتيادية بين الفهم والتطبيق
التعلم للفهم:
عند تدريس الكسور، من المهم التركيز على الفهم الحقيقي وليس حفظ القواعد.
التعلم للفهم يعني أن الطالب:
1- يدرك معنى الكسر.
2- كيفية استخدامه في الحياة اليومية،
3- لماذا نستخدمه بهذه الطريقة.
أولاً: ما الكسر؟
أحد معاني الكسر انه يمثل جزءاً من كل.( وحدة )
إذا قسمنا شيئاً إلى أجزاء متساوية وأخذنا بعضاً منها، فإننا نكتب ذلك على شكل كسر.
مثال 1:
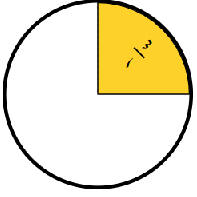
لديك لوح شوكولاتة مقسّم إلى 10- قطع متساوية، أكلت 3 قطع.

• ما الجزء الذي أكلته؟
• الجواب: 3 من 10 أجزاء =
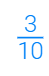
ثانياً: أنواع الكسور
1. كسر بسيط: البسط أصغر من المقام
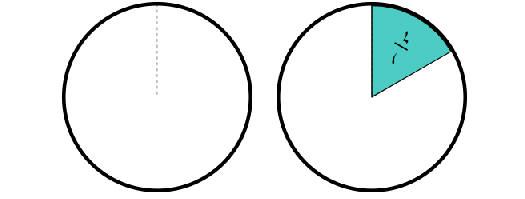
مثال:سدس
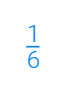
2. كسر غير فعلي: البسط أكبر من أو يساوي المقام
مثال:
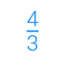
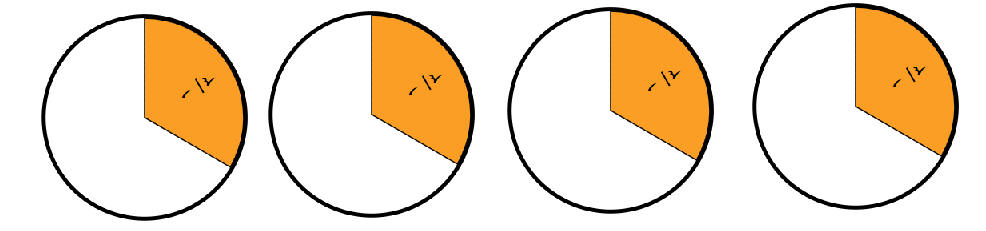
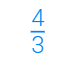
3. عدد كسري: عدد صحيح مع كسر
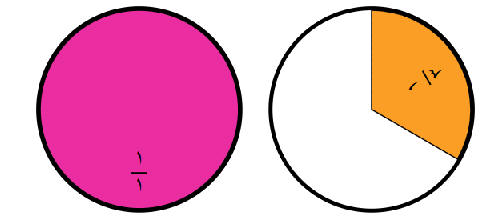
مثال:
1و ثلث
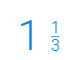
مهارة تحويل الكسور
مثال 4: تحويل عدد كسري إلى كسر غير فعلي
حوّل 2 وثلث إلى كسر غير فعلي:
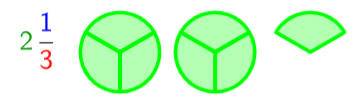
• اضرب العدد الصحيح في المقام: 2 × 3 = 6
• أضف البسط: 6 + 1 = 7
• الجواب:سبعة أثلاث


أولاً: المعاني المختلفة للكسر
رغم أن الكسر يُعرَّف غالبًا على أنه “جزء من كل”، إلا أن له عدة معانٍ تعتمد على السياق:
1. جزء من كل ( وحدة )
|
|
|
• مثال: ¼ تعني جزء واحد من 4 أجزاء متساوية من شيء كامل.اجزاء من بيتزا واحدة.
2. نسبة (مقارنة بين كميتين)
النسبة هي مقارنة بين مقدارين.
• مثال: إذا صندوق فيه 10 خناقس، وصندوق آخر به ٢٠ ضفدع
|
|
|
فنسبة العدد في الصندوق الأول إلى العدد في الصندوق الثاني هي النصف .
3. عملية قسمة
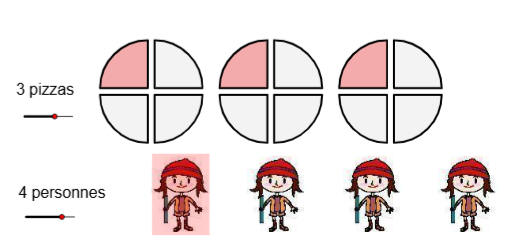
4 أشخاص أكلوا 3 حبات بيتزا ما نصيب الفرد؟
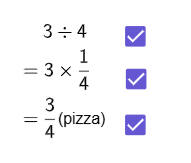
• الكسر يمكن قراءته كـ “بسط ÷ مقام”.
• مثال: ¾ = 3 ÷ 4
4. عدد على خط الأعداد.
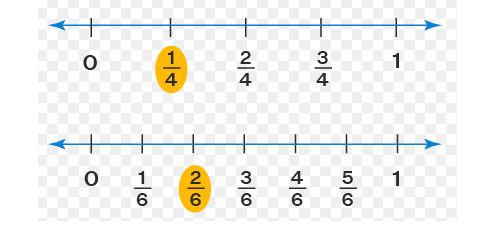
• الكسر يمثل موقعًا على خط الأعداد، بين عددين صحيحين.
• مثال: السدسين يقع بين سدس و3أسداس
5. جزء من مجموعة (علاقة بين عناصر مجموعة ).
• طبق بيض مكون من ست بيضات ٤ بيضات فاسدات . ثلثي البيض فاسد .
كرتون شوكولاتة فيه 6 قوالب شكولاتة

كل قالب يمثل سدس
ثانياً: العمليات على الكسور

1. الجمع
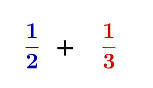
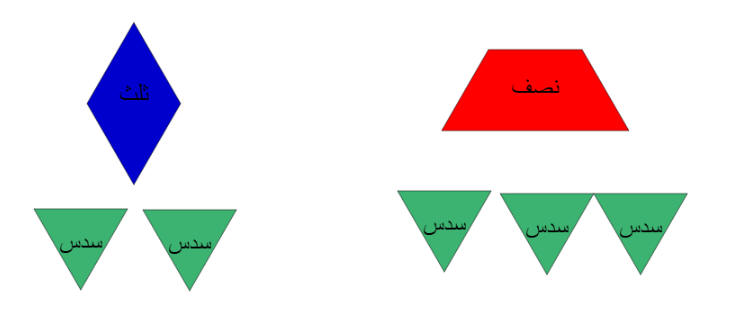
فهم العملية:
• نجمع أجزاء متساوية.
• ضروري أن تكون المقامات متساوية.
مثال:
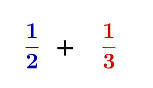
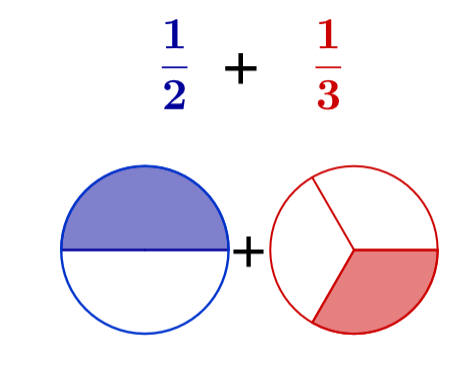
جمع وطرح عددين كسريين
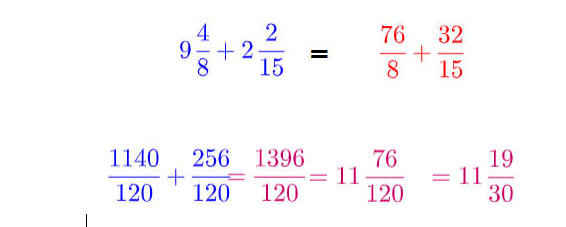
مثال ثاني

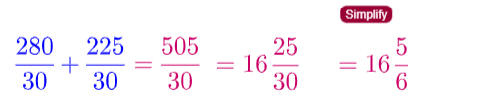
جمع وطرح عددين كسريين
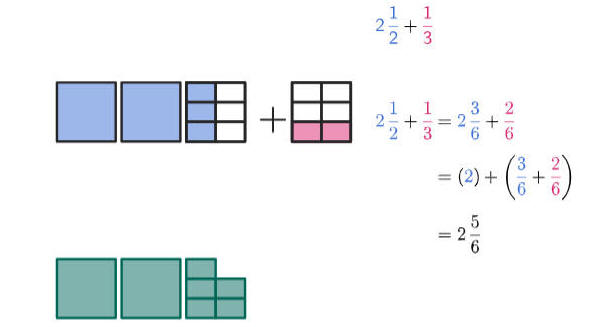
2. الطرح
فهم العملية:
• نطرح جزءًا من آخر بنفس المقام. أو مقامين مختلفين
مثال:

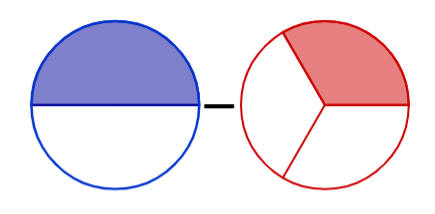
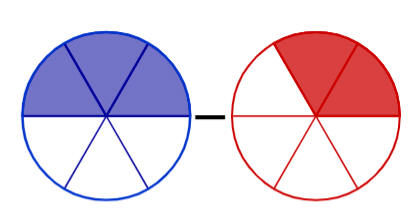
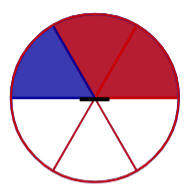
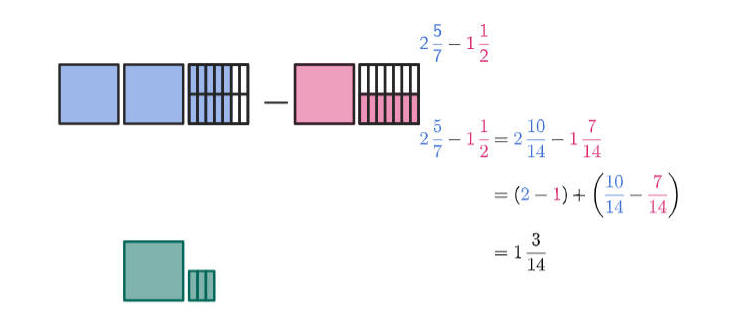
خطوات:
• نوحد المقام:
طرح عددين كسريين
3. الضرب
فهم العملية:
• نأخذ جزءًا من جزء.
مثال:
½ × ⅔
نصف الثلثين
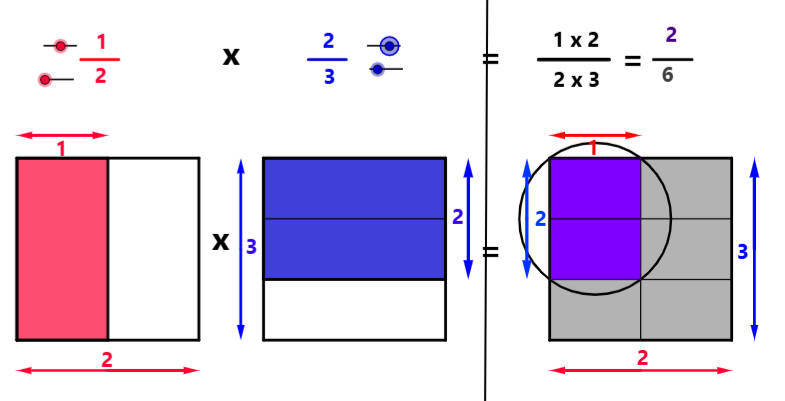
الخطوات:
١- نمثل الواحد بمستطيل احد بعديه مقام الكسر الأول والبعد الآخر مقام الكسر
الثاني
٢- نمثل
الثلثين
٣- نأخذ نصف الثلثين
🟦🟦🟦
🟦🟦🟦
الواحد ٦ مربعات
نمثل النصف
🟦🟦🟦
نأخد ثلثي هذا النصف
ثلثي النصف = ٢ مربع
وهي تمثل ثلث الوحد
النتيجة: ²⁄₆ = ⅓
====================================================================
=====================================================================
ضرب عددين كسريين
مثال :
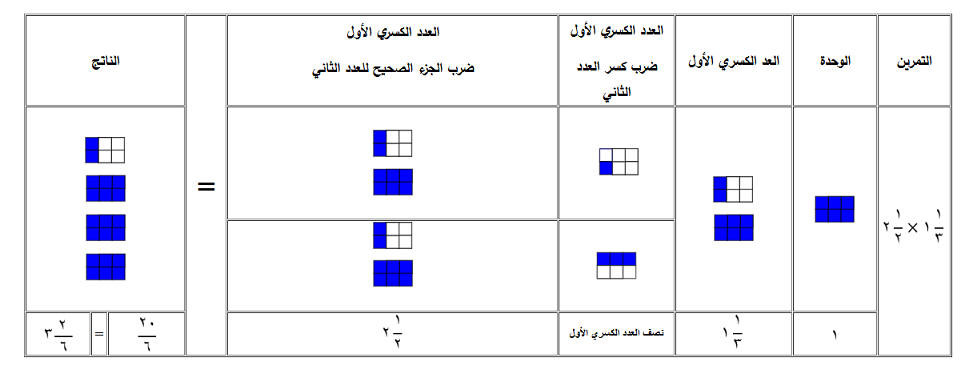
الطريقة :
أولاً: الفكرة تعتمد على قاعدة توزيع الضرب على الجمع :
أ ( ب+ ج ) = أ ب + أ ج
حيث أ= العدد الكسري الأول
حيث ب = كسر العدد الثاني
حيث ج = الجزء الصحيح من العدد الثاني
أولاً: نقوم ببناء مستطيل بعده الأول مقام العدد الكسري الأول والبعد الثاني مقام العدد الكسري الثاني.
ثانياً: نمثل العدد الكسري الأول
ثالثا : نمثل حاصل ضرب العدد الكسري الأول في كسر العدد الكسري الثاني
نمثل حاصل ضرب ضرب العدد الكسري الأول في الجزء الصحيح من العدد الكسري الثاني
رابعا ً: نجمع عدد المربعات في كل منهما
ملاحظة : في حال احتاج الناتج إلى تبسيط نقوم بعملية التبسيط وفي حال كون المجموع أكثر من الوحدة نكون وحدة جديدة .
4. القسمة
معنى القسمة :
• القسمة تعني كم مرة يحتوي المقسوم عليه داخل المقسوم .
مثال 1:
نصف على سدس
المعنى كم سدس موجود بالنصف
مثال2:
ثلث على سدس
المعنى كم سدس موجود بالثلث

قسمة كسرين برمجية أخرى
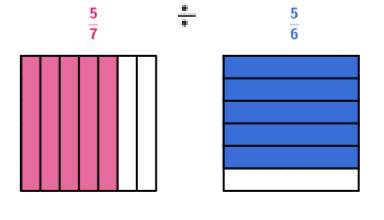
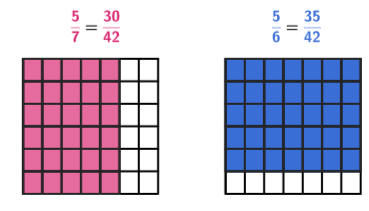
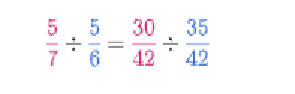
طريقة سريعة لقسمة كسر على كسر بدون توحيد المقامين
( بسط الأول x مقام الثاني )
----------------------------
( بسط الثاني x مقام الأول )