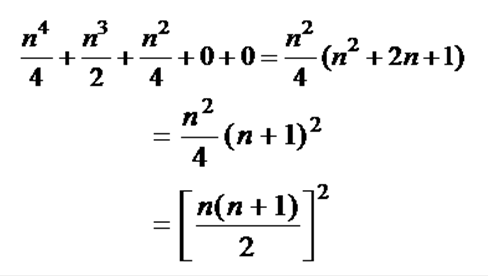
رابعاً: عندما نصل إلى عدد ثابت في الفرق الثالث

في هذه الحالة فإن الحد النوني للمتتابعة سيمثل معادلة من الدرجة الثالثة على الصورة:

مثال: (متتابعة مجموع الأعداد المكعبة)

مثال: لنأخذ المتتابعة التالية:

1,9,36,100 ,225….

التي تمثل مجموع متتابعة الأعداد المكعبة.

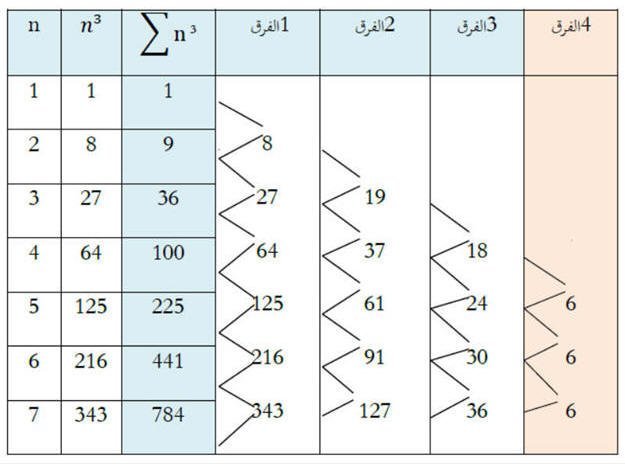
لإيجاد الحد النوني لهذه المتتابعة بطريقة الفروق نمثل المتتابعة كما يلي:

وبما أن الفرق الرابع ثابت فإن معادلة الحد النوني من الدرجة الرابعة وتكتب معادلتها بالصورة :

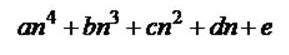
وبالتعويض عن قيمة n في هذه المعادلة بالأعداد :1 ، 2 ، 3 ، 4 ، 5 على التوالي نحصل على المعادلات الخمس التالية :

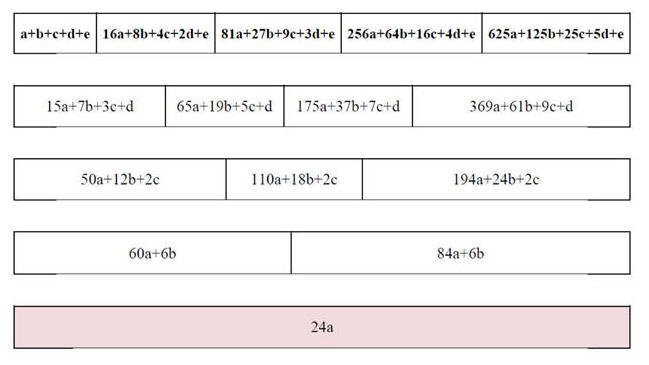
وبمقارنة هذه المعادلات بالفروق السابقة نحصل على قيم المعاملات في المعادلة السابقة ، كما يلي:

بالتعويض عن قيمة a في أول حدود الفرق الثالث

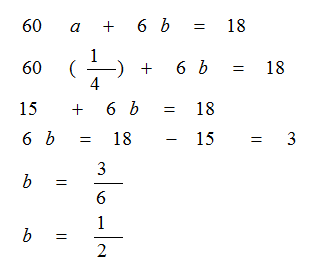
وبالتعويض عن قيمتي a,b في أول حدود الفرق الثاني

وبالتعويض عن قيم a,b,c في أول حدود الفرق الأول للمتتابعة

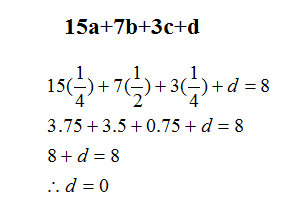
وبتعويض قيم a,b,c,d في أول حدود المتتابعة:

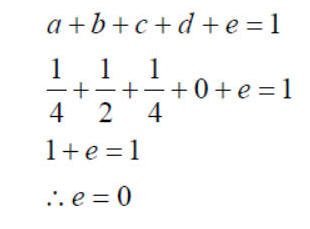
وبتعويض هذه القيم (a,b,c,d,e)في  معادلة الدرجة الرابعة نحصل على التالي :