برمجية أعواد الكبريت
هذه البرمجية لها تطبيقات في
المتسلسلات الرياضية بشكل كبير، وحل المشكلات حيث تطلب منك البرمجيات اختيار شكل
من الأشكال الأساسية والتي يتم من خلالها عمل أنماط بهذه الأشكال والمطلوب منك
تعبئة الجدول ببعض الحدود، ومن ثم محاولة استخدام الجبر لاكتشاف قاعدة النمط رياضياً
، وعند كتابة القاعدة ستعطيك البرمجية تغذية راجعة بصحة الحل وتوضح الاجابات
الصحيحة :
الواجهة الرئيسية للبرمجية
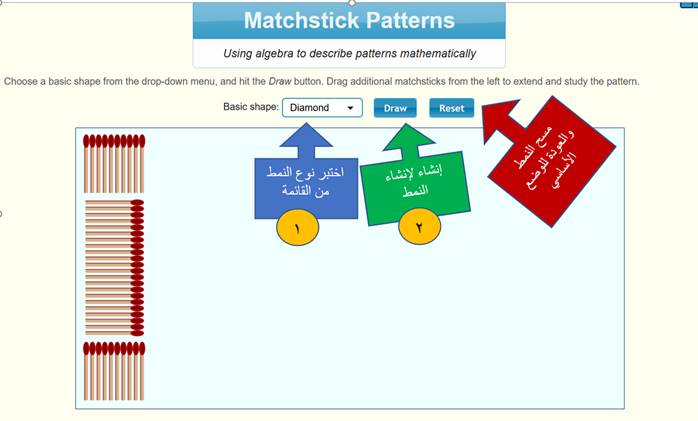
تستطيع اختيار نوع الشكل من القائمة الموجودة ![]() ثم إنشاء هذا الشكل بالضغط
على زر
ثم إنشاء هذا الشكل بالضغط
على زر ![]() وبعد إنشاء النمط يمكنك
متابعة الحدود وتسجيل هذه الحدود في الجدول التالي :
وبعد إنشاء النمط يمكنك
متابعة الحدود وتسجيل هذه الحدود في الجدول التالي :
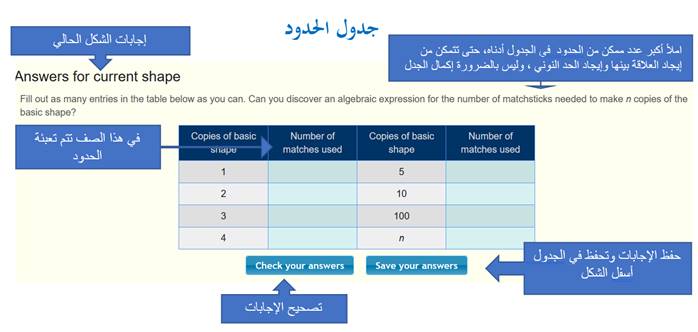
في
هذا الجدول يمكن تعبئة عدد الأعواد في كل حد فعدد أعداد الحد الأول يوضع أمام رقم
1 ، وعدد الأعواد في الحدين الاول والثاني توضع أمام 2 ، وبالمثل بقية الحدود ،
حتى تصل للحد النوني ويوضح أمام n ، وبعد الانتهاء
يمكنك التحقق من حلك بالضغط على ![]() وستظهر الإجابات الصحيحة والإجابات الخاطئة وفي
حال الوصل للقاعدة ،يمكنك حفظ الإجابة بالضغط على زر
وستظهر الإجابات الصحيحة والإجابات الخاطئة وفي
حال الوصل للقاعدة ،يمكنك حفظ الإجابة بالضغط على زر ![]() وسيحفظ الحل في الجدول التالي :
وسيحفظ الحل في الجدول التالي :
جدول الحفظ
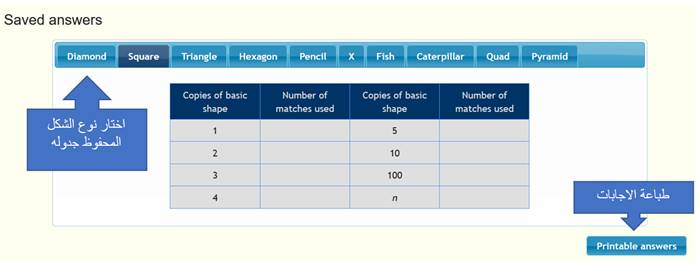
في
هذا الجدول يمكنك استعراض اجاباتك المحفوظة على جميع الأشكال من خلال اختيار نوع
الشكل من الأعلى وإذا رغبت في طباعة الأشكال يمكنك ذلك بالضغط على زر ![]() وسيعرض لك ملف يحتوي جميع اجابات الأشكال مع
تصحيحها.
وسيعرض لك ملف يحتوي جميع اجابات الأشكال مع
تصحيحها.
وسنستعرض
هذه الاشكال مع حلول كل قاعدة كل شكل، كما يلي
المعين Diamond
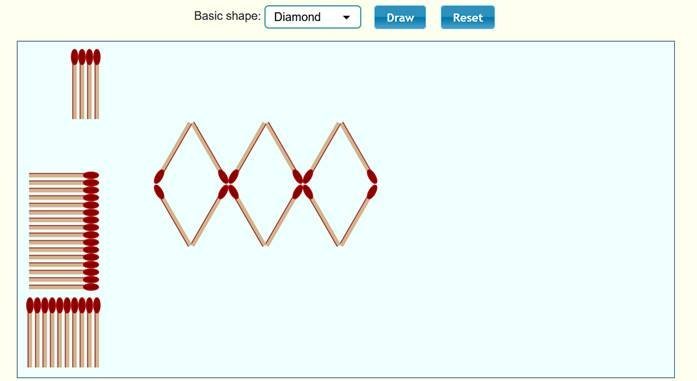
نلاحظ
أن الحد الأول 4 ، والحد الثاني 8 ، والحد الثالث 12 ، ونكمل الجدول :
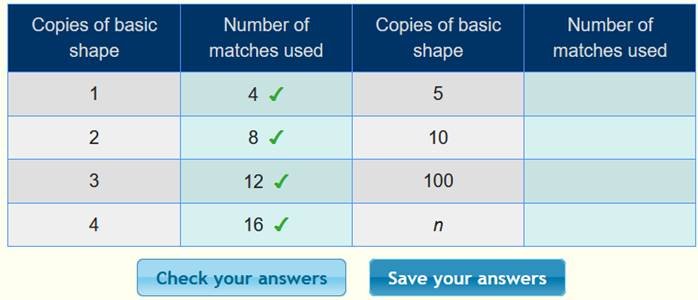
بعد
التأكد من صحة الحدود ، نبحث القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
4 |
8 |
12 |
16 |
||
|
الفرق الأول |
8-4 = 4 |
12-8=4 |
16-12=4 |
|||
نلاحظ أن الفرق الأول، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى ، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=4
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن
بقيمة a في ( الجدول 2) ونساويها بقيمتها في ( الجدول 1)
a+c= 4 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
4+c=4
بحل المعادلة نجد أن قيمة c
تساوي صفر ، ونعوض في صيغة المعادلة الرئيسية
كما يلي :
an+c
نستبدل
a بقيمتها 4
، و c بقيمتها
صفر لإيجاد الحد النوني وهو كالتالي :
الحد النوني = 4n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
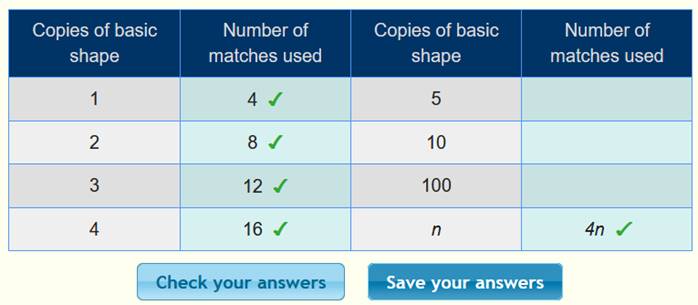
المــــــــربع Square
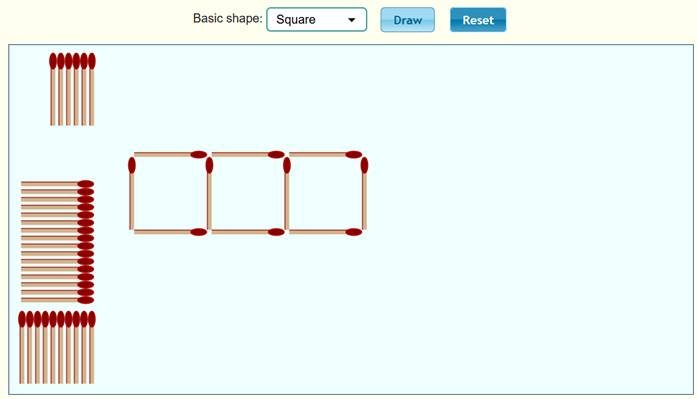
نلاحظ
أن الحد الأول 4 ، والحد الثاني 7 ، والحد الثالث 10 ، ونكمل الجدول :
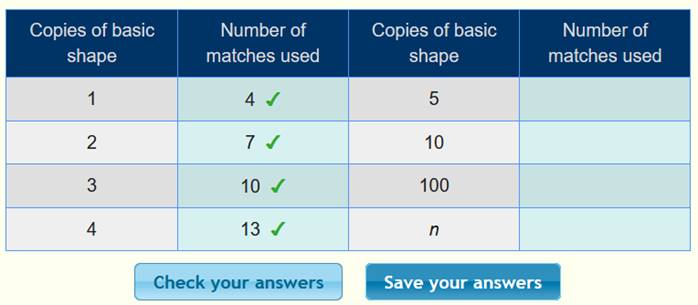
بعد
التأكد من صحة الحدود ، نبحث عن القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
4 |
7 |
10 |
13 |
||
|
الفرق الأول |
7-4=3 |
10-7=3 |
13-10=3 |
|||
نلاحظ أن الفرق الأول ، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
A |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=3
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن c بقيمة a في ( الجدول 2)
ونساويها بقيمتها في ( الجدول 1)
a+c= 4 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
3+c=4
c=1
بحل المعادلة نجد أن قيمة c
تساوي 1 ، ونعوض في صيغة المعادلة الرئيسية كما
يلي :
an+c
نستبدل
a بقيمتها 3
، و c بقيمتها 1 لإيجاد الحد النوني
وهو كالتالي :
الحد النوني =+1 3n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
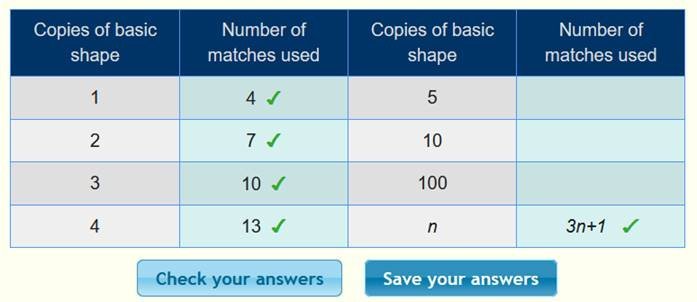
المثلث Triangle
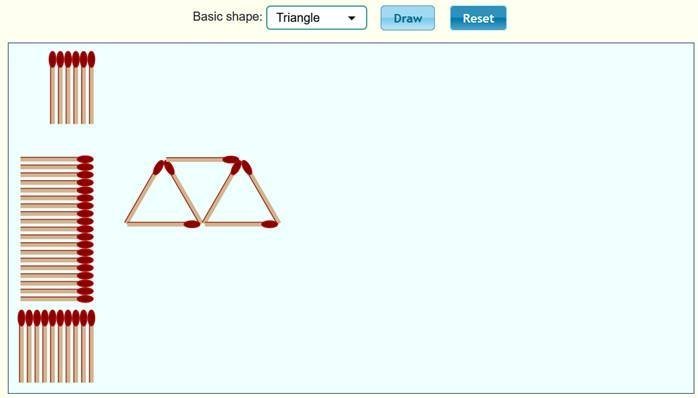
نلاحظ
أن الحد الأول 3 ، والحد الثاني 5 ، والحد الثالث 7 ، ونكمل الجدول :
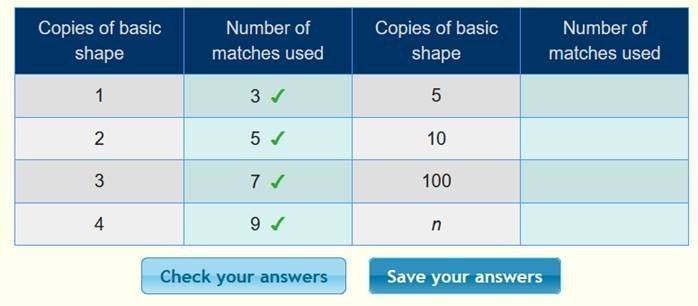
بعد
التأكد من صحة الحدود ، نبحث عن القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
3 |
5 |
7 |
9 |
||
|
الفرق الأول |
5-3=2 |
7-5=2 |
9-7=2 |
|||
نلاحظ أن الفرق الأول ، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=2
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن c بقيمة a في ( الجدول 2)
ونساويها بقيمتها في ( الجدول 1)
a+c= 3 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
2+c=3
c=1
بحل المعادلة نجد أن قيمة c
تساوي 1 ، ونعوض في صيغة المعادلة الرئيسية كما
يلي :
an+c
نستبدل
a بقيمتها 2
، و c بقيمتها 1 لإيجاد الحد النوني
وهو كالتالي :
الحد النوني =+1 2n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
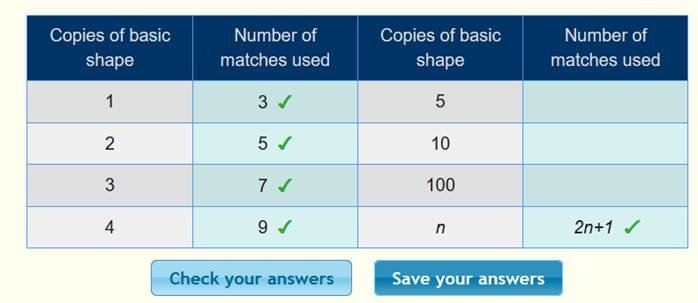
السداسي Hexagon
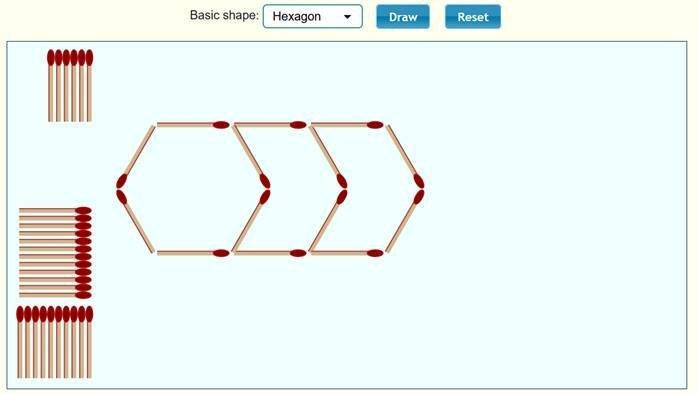
نلاحظ
أن الحد الأول 6 ، والحد الثاني 10 ، والحد الثالث 14 ، ونكمل الجدول :
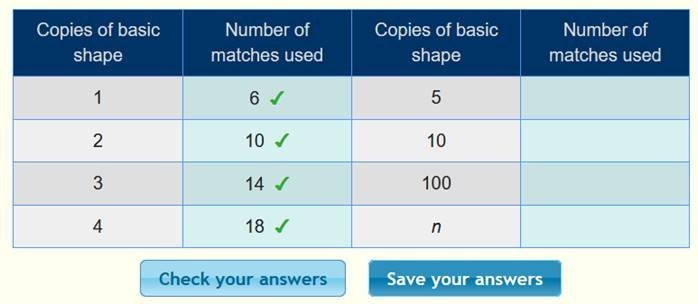
بعد
التأكد من صحة الحدود ، نبحث عن القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
6 |
10 |
14 |
18 |
||
|
الفرق الأول |
10-6=4 |
14-10=4 |
18-14=4 |
|||
نلاحظ أن الفرق الأول ، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=4
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن c بقيمة a في ( الجدول 2)
ونساويها بقيمتها في ( الجدول 1)
a+c= 6 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
4+c=6
c=2
بحل المعادلة نجد أن قيمة c
تساوي 2 ، ونعوض في صيغة المعادلة الرئيسية كما يلي :
an+c
نستبدل
a بقيمتها 4 ، و c بقيمتها 2 لإيجاد الحد النوني وهو كالتالي :
الحد النوني =+2 4n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
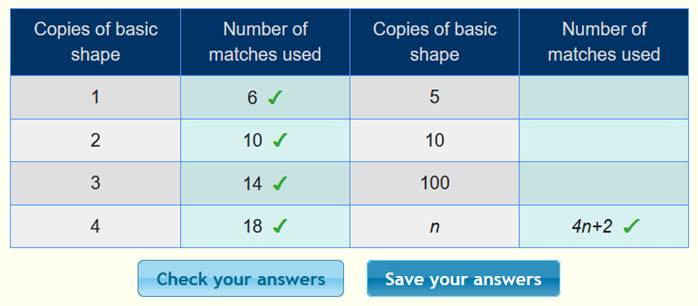
قلم الرصاص
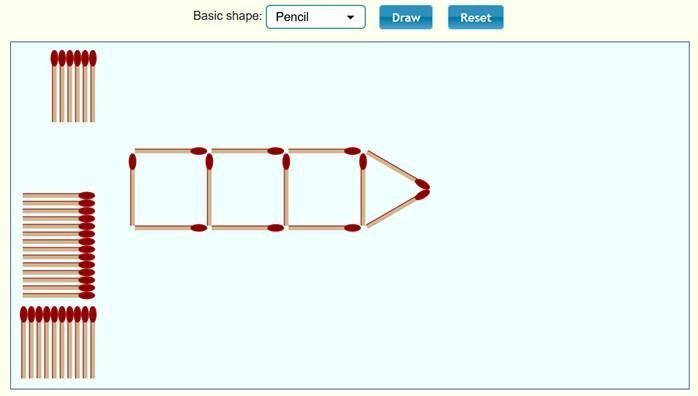
نلاحظ
أن الحد الأول 6 ، والحد الثاني 9 ، والحد الثالث 12 ، ونكمل الجدول :
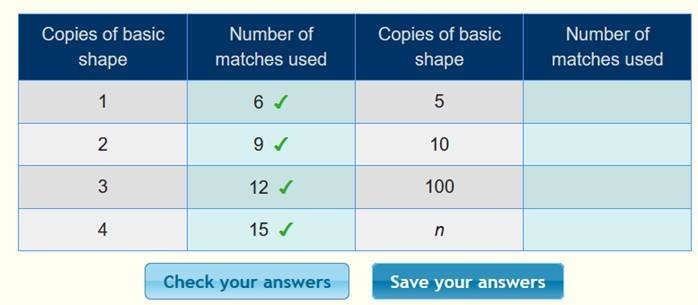
بعد
التأكد من صحة الحدود ، نبحث عن القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
6 |
9 |
12 |
15 |
||
|
الفرق الأول |
9-6=3 |
12-9=3 |
15-12=3 |
|||
نلاحظ أن الفرق الأول ، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=3
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن c بقيمة a في ( الجدول 2)
ونساويها بقيمتها في ( الجدول 1)
a+c= 6 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
3+c=6
c=3
بحل المعادلة نجد أن قيمة c
تساوي 3 ، ونعوض في صيغة المعادلة الرئيسية كما يلي :
an+c
نستبدل
a بقيمتها 3 ، و c بقيمتها 3 لإيجاد الحد النوني وهو كالتالي :
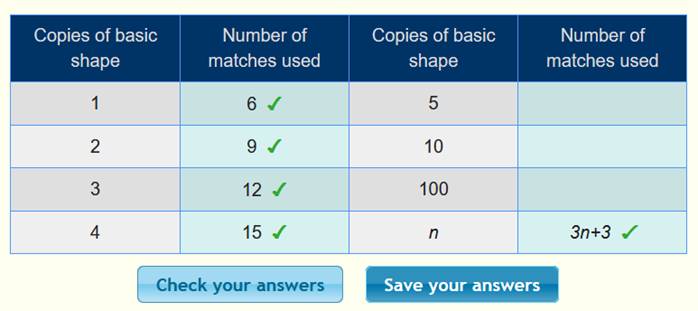
الحد النوني =+3 3n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
الشكل X
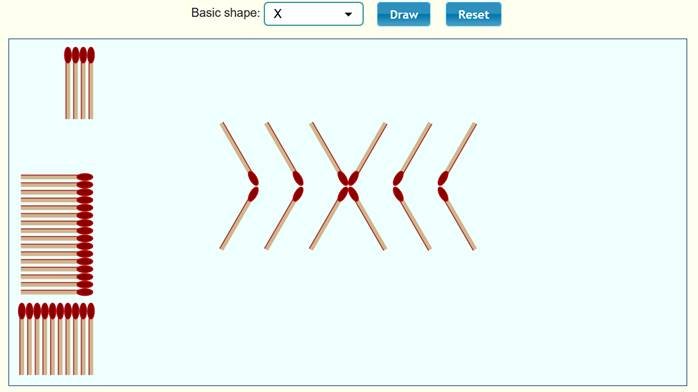
نلاحظ
أن الحد الأول 4 ، والحد الثاني 8 ، والحد الثالث 12 ، ونكمل الجدول :

بعد
التأكد من صحة الحدود ، نبحث القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
4 |
8 |
12 |
16 |
||
|
الفرق الأول |
8-4 = 4 |
12-8=4 |
16-12=4 |
|||
نلاحظ أن الفرق الأول، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى ، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=4
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن
بقيمة a في ( الجدول 2) ونساويها بقيمتها في ( الجدول 1)
a+c= 4 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
4+c=4
بحل المعادلة نجد أن قيمة c
تساوي صفر ، ونعوض في صيغة المعادلة الرئيسية
كما يلي :
an+c
نستبدل
a بقيمتها 4
، و c بقيمتها
صفر لإيجاد الحد النوني وهو كالتالي :
الحد النوني = 4n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :

شكل السمكة Fish
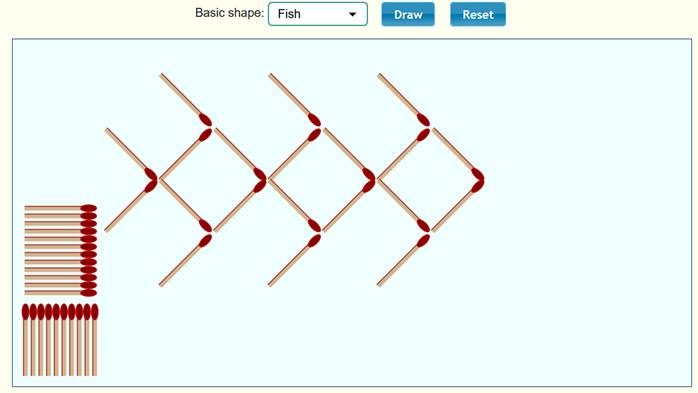
نلاحظ
أن الحد الأول 8 ، والحد الثاني 14 ، والحد الثالث 20 ، ونكمل الجدول :
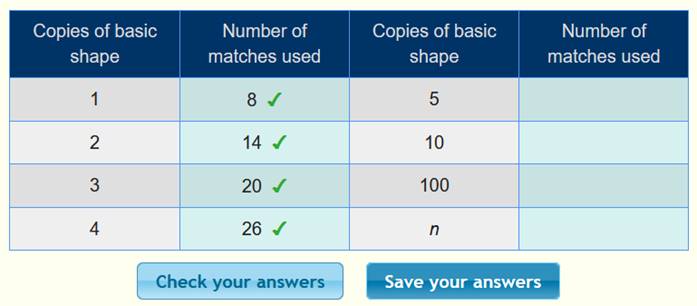
بعد
التأكد من صحة الحدود ، نبحث القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
8 |
14 |
20 |
26 |
||
|
الفرق الأول |
14-8=6 |
20-14=6 |
26-20=6 |
|||
نلاحظ أن الفرق الأول، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى ، أي ستكون
على الشكل : an+c
، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=6
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول عن
بقيمة a في ( الجدول 2) ونساويها بقيمتها في ( الجدول 1)
a+c= 8 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
6+c=8
بحل المعادلة نجد أن قيمة c
تساوي 2 ، ونعوض في صيغة المعادلة الرئيسية كما
يلي :
an+c
نستبدل
a بقيمتها 6
، و c بقيمتها 2
لإيجاد الحد النوني وهو كالتالي :
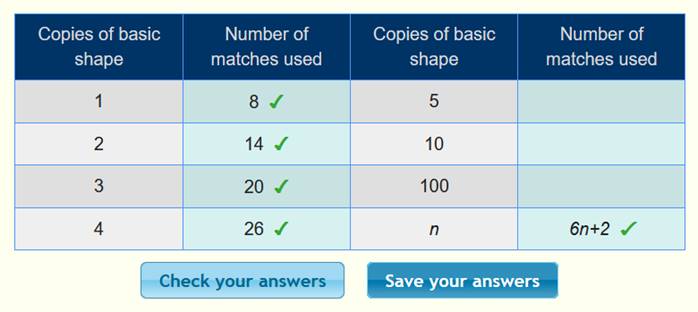
الحد النوني =+2 6n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
شكل اليرقــة
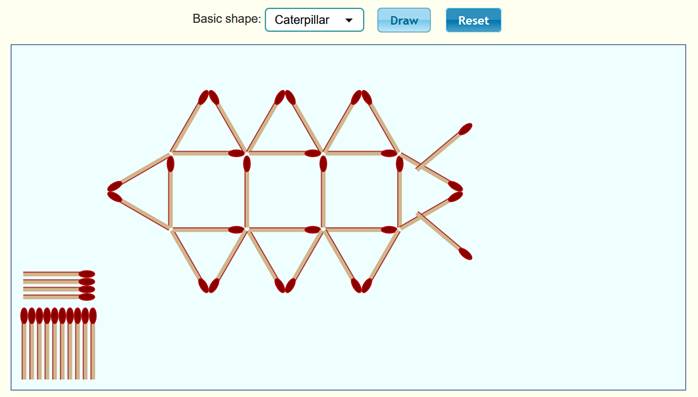
نلاحظ
أن الحد الأول 14 ، والحد الثاني 21 ، والحد الثالث 28 ، ونكمل الجدول :
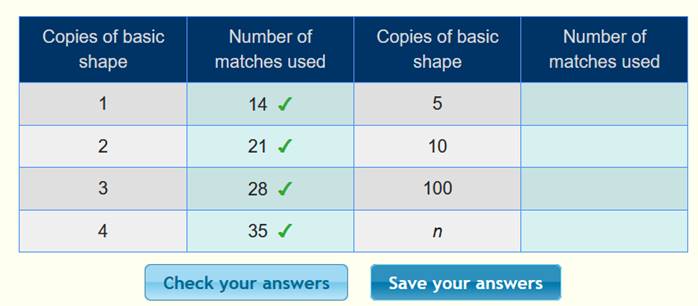
بعد
التأكد من صحة الحدود ، نبحث القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
عدد الأعواد |
14 |
21 |
28 |
35 |
||
|
الفرق الأول |
21-14=7 |
28-21=7 |
35-28=7 |
|||
نلاحظ أن الفرق الأول، ثابت بين جميع الحدود ،
إي يمكن استخدام هذا الفرق لإيجاد القاعدة ، كالتالي:
نلاحظ
أن الحد الأول هو الثابت وهذا يعني أن المعادلة ستكون من الدرجة الأولى ، أي ستكون
على الشكل : an+c ، نعوض في المعادلة بقيم n
ونوجد الحدود كما يلي :
|
n |
1 |
2 |
3 |
4 |
||
|
an+c |
a+c |
2a+c |
3a+c |
4a+c |
||
|
الفرق الأول |
a |
a |
a |
|||
الان
نساوي الفرق الأول في المعادلة( جدول 2) بالفرق الأول في الأعداد ( جدول 1)كما يلي
:
a=7
الأن
نحتاج إيجاد قيمة c ، فنعوض في الحد الأول
بقيمة a في ( الجدول 2) ونساويها بقيمتها في ( الجدول 1)
a+c= 14 ( الحد الأول نساويه بالأول)
الآن
نعوض بقيمة a كما يلي :
7+c=14
بحل المعادلة نجد أن قيمة c
تساوي 7 ، ونعوض في صيغة المعادلة الرئيسية كما
يلي :
an+c
نستبدل
a بقيمتها 7 ، و c بقيمتها 7
لإيجاد الحد النوني وهو كالتالي :
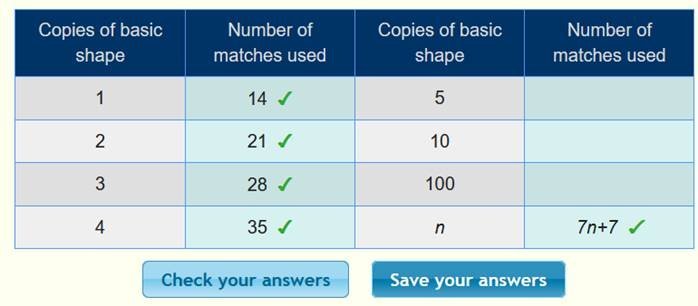
الحد النوني =+7 7n
ونعوض
في الجدول لنتأكد من صحة الحل كما يلي :
المربع
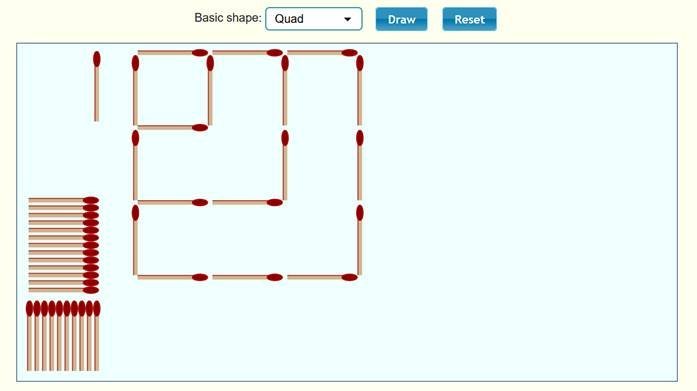
نلاحظ
أن الحد الأول 4 ، والحد الثاني 10 ، والحد الثالث 18 ، ونكمل الجدول :
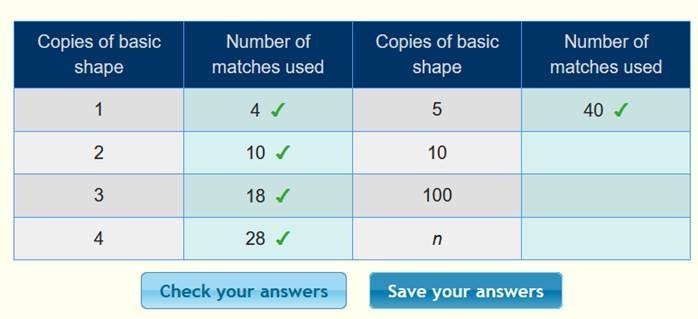
بعد
التأكد من صحة الحدود ، نبحث القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
5 |
|||||
|
عدد الأعواد |
4 |
10 |
18 |
28 |
40 |
|||||
|
الفرق الأول |
10-4=6 |
18-10=8 |
28-18=10 |
40-28=12 |
||||||
|
الفرق
الثاني |
8-6=2 |
10-8=2 |
12-10=2 |
|||||||
نلاحظ
أن الفرق الأول لم يكن ثابت ، فأوجدنا
الفرق الثاني وكان ثابت ، والآن نستخدم هذا الفرق لإيجاد القاعدة ( قانون
الحد النوني ) كما يلي :
بما
أن الفرق الثاني هو الثابت ستكون معادلة من الدرجة الثانية والتي صيغتها على كما
يلي :
an2 +bn+c
نعوض
بقيمة n في الجدول التالي لنوجد
الحدود ثم نطبق على المعادلة نفس الذي طبق على الحدود في الجدول السابق كما يلي :
|
n |
1 |
2 |
3 |
4 |
5 |
|||||
|
an2 +bn+c |
a+b+c |
4a+2b+c |
9a+3b+c |
16a+4b+c |
25a+5+c |
|||||
|
الفرق الأول |
3a+b |
5a+b |
7a+b |
9a+b |
||||||
|
الفرق
الثاني |
2a |
2a |
2a |
|||||||
الأن
نساوي الفرق الثاني في ( الجدول 2) بالفرق الثاني في ( الجدول 1) لإيجاد قيمة a كما يلي :
2a=2
a=1
بحل
المعادلة نجد أن قيمة a تساوي 1
الآن
نوجد قيمة b بالتعويض بمساوات الفرق الأول والحد الأول في (الجدول2) مع الفرق الأول في الحد الأول في ( الجدول الأول )
، كما يلي :
3a+b=6 ( ساوين الحد الأول مع الأول)
الآن
نعوض بقيمة a = 1 كما يلي :
3(1)+b=6
3+b=6
b=3
بحل
المعادلة وجدنا أن قيمة b تساوي ثلاثة ، الأن نوجد قيمة c
،
وذلك بمساواة الحد الأول في ( الجدول 1) مع الحد الأول في( الجدول 2) كما يلي
a+b+c=4
نعوض
بقيم a=1 و b=3 فنجد أن
1+3+c=4
4+c=4
c=0
وبحل
المعادلة نجد أن قيمة c=0 ،
الآن
نعوض بقيمة a=1 و b=3 و c=0 في الصيغة
العامة لمعادلة الدرجة الثانية وهي :
an2
+bn+c
(1)n2
+(3)n+(0)
فنجد
أن صيغة الحد النوني هي :
n2 +3n
وللتأكد
نعوض في الجدول كما يلي :
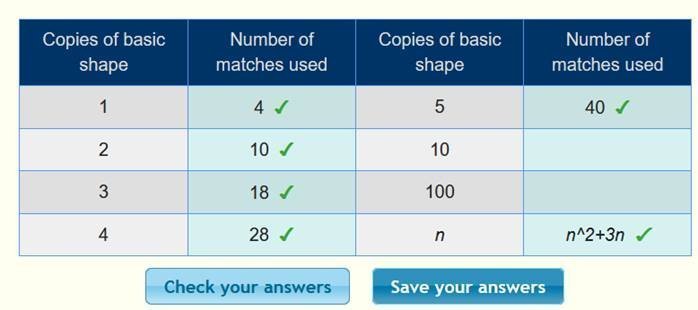
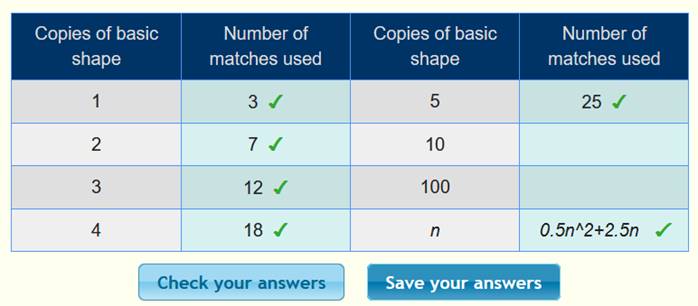
الهـــــــرم Pyramid
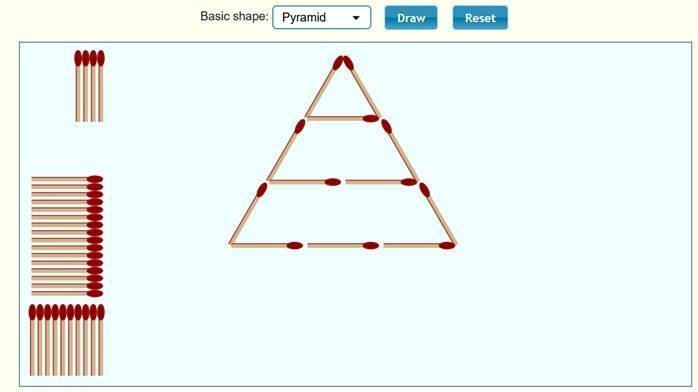
نلاحظ
أن الحد الأول 3 ، والحد الثاني 7 ، والحد الثالث 12 ، ونكمل الجدول :
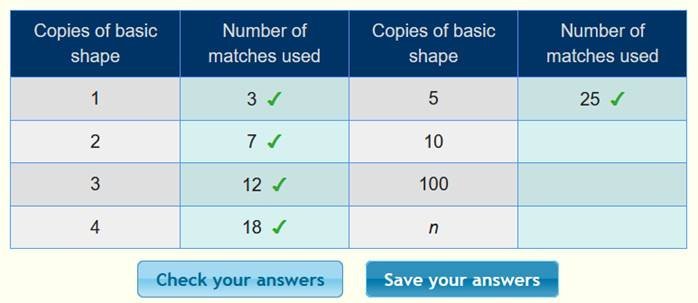
بعد
التأكد من صحة الحدود ، نبحث القاعدة كما يلي :
أولاً
نوجد الفروق كما يلي :
|
n |
1 |
2 |
3 |
4 |
5 |
|||||
|
عدد الأعواد |
3 |
7 |
12 |
18 |
25 |
|||||
|
الفرق الأول |
4 |
5 |
6 |
7 |
||||||
|
الفرق
الثاني |
1 |
1 |
1 |
|||||||
نلاحظ
أن الفرق الأول لم يكن ثابت ، فأوجدنا
الفرق الثاني وكان ثابت ، والآن نستخدم هذا الفرق لإيجاد القاعدة ( قانون
الحد النوني ) كما يلي :
بما
أن الفرق الثاني هو الثابت ستكون معادلة من الدرجة الثانية والتي صيغتها على كما
يلي :
an2 +bn+c
نعوض
بقيمة n في الجدول التالي لنوجد
الحدود ثم نطبق على المعادلة نفس الذي طبق على الحدود في الجدول السابق كما يلي :
|
n |
1 |
2 |
3 |
4 |
5 |
|||||
|
an2 +bn+c |
a+b+c |
4a+2b+c |
9a+3b+c |
16a+4b+c |
25a+5+c |
|||||
|
الفرق الأول |
3a+b |
5a+b |
7a+b |
9a+b |
||||||
|
الفرق
الثاني |
2a |
2a |
2a |
|||||||
الأن
نساوي الفرق الثاني في ( الجدول 2) بالفرق الثاني في ( الجدول 1) لإيجاد قيمة a كما يلي :
2a=1
a=0.5
بحل
المعادلة نجد أن قيمة a تساوي نصف
الآن
نوجد قيمة b بالتعويض بمساوات الفرق الأول والحد الأول في (الجدول2) مع الفرق الأول في الحد الأول في ( الجدول 1 ) ،
كما يلي :
3a+b=4 ( ساوين الحد الأول مع الأول)
الآن
نعوض بقيمة a = 0.5 كما يلي :
3(0.5)+b=4
(1.5)+b=4
b=2.5
بحل
المعادلة وجدنا أن قيمة b تساوي ثلاثة ، الأنن نوجد قيمة c
،
وذلك بمساواة الحد الأول في ( الجدول 1) مع الحد الأول في( الجدول 2) كما يلي
a+b+c=4
نعوض
بقيم a=0.5 و b=2.5 فنجد أن
0.5+2.5+c=3
3+c=3
c=0
وبحل
المعادلة نجد أن قيمة c=0 ،
الآن
نعوض بقيمة a=0.5 و b=2.5 و c=0 في الصيغة
العامة لمعادلة الدرجة الثانية وهي :
an2
+bn+c
(0.5)n2
+(2.5)n+(0)
فنجد
أن صيغة الحد النوني هي :
0.5n2 +2.5n
وللتأكد
نعوض في الجدول كما يلي :