نشاط 1
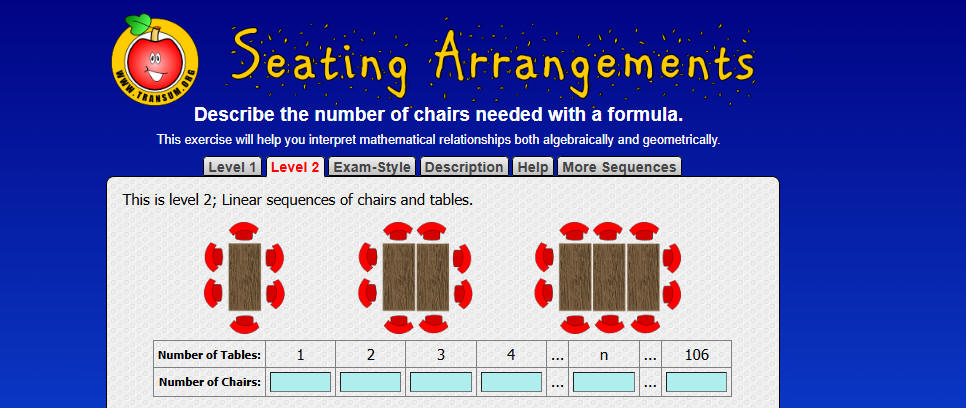
ما العلاقة بين عدد الطاولات وعدد الكراسي

ما العلاقة بين عدد الطاولات وعدد الكراسي
نشاط 2
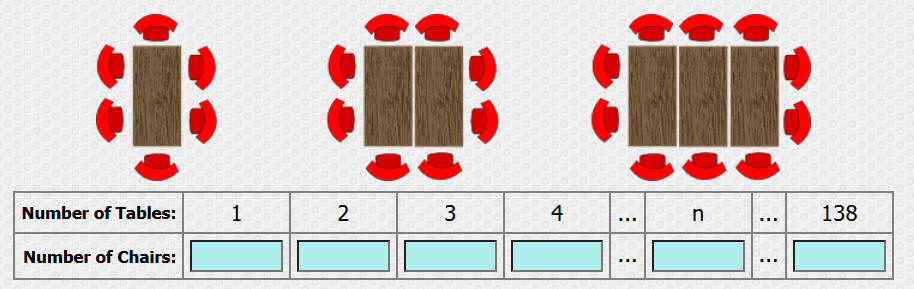
ما العلاقة بين عدد الطاولات وعدد الكراسي
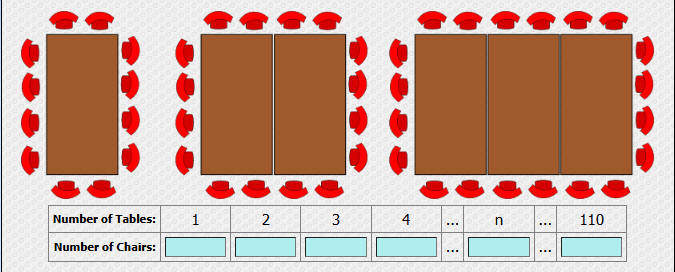
لمعرفة العلاقة بين عدد الطاولات وعدد الكراسي نبني جدول يربط
بين عدد الطاولات وعدد الكراسي
| الطاولات | عدد الكراسي | الفرق |
| 1 | 12 | 4 |
| 2 | 16 | 4 |
| 3 | 20 | 4 |
| 4 | 24 | 4 |
| 5 | 28 | 4 |
| 6 | 32 | 4 |
| n | 4n+8 | |
الفرق =4
القاعدة
الحد الأول = الفرق + ؟
12= 4+ ؟
؟=8
القاعد= 4n+8
n=عدد الطاولات
الضغط على

يعطي تمرين جديد
نشاط
لمعرفة مجموع عدد الكراسي في مجموع محدد من الطاولات
ما مجموع عدد الكرسي في مطعم به عشر ترتيبات من الطاولات

نبني الجدول
| الطاولات |
عدد الكراسي |
مجموع الكراسي |
| 1 | 12 | 12 |
| 2 | 16 | 28 |
| 3 | 20 | 48 |
| 4 | 24 | 72 |
| 5 | 28 | 100 |
| 6 | 32 | 132 |
| n | 4n+8 | 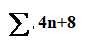 |
معلوم أن
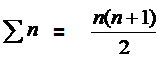
نحسب
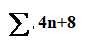
لمعرفة مجموع من واحد الى ستة نعوض
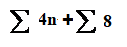
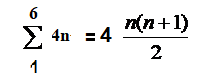
+
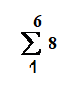
نعوض في المقدار
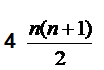
n=6
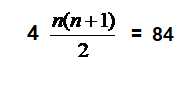
+
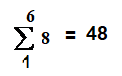
المجموع= 132
| 6 | 32 | 132 |
لمعرفة خمس ترتيبات نعوض عن n=5
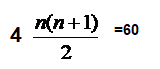
+
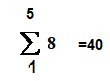
= 100
التأكد من الجدول السابق
| 5 | 28 | 100 |
==================================================================================================
القاعدة بقانون الفروق
| الطاولات |
عدد الكراسي |
مجموع الكراسي | لفرق الأول | الفرق الثاني |
| 1 | 12 | 12 | 16 | 4 |
| 2 | 16 | 28 | ||
| 3 | 20 | 48 | 20 | |
| 4 | 24 | 72 | 24 | 4 |
| 5 | 28 | 100 | 28 | 4 |
| 6 | 32 | 132 | 32 | 4 |
| n | 4n+8 | 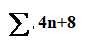 |
||
المعادلة من الدرجة الثانية
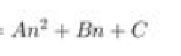
نعوض في n
l 2 3
A+B +C 4A+2B+C 9A+3B+C
3A+B 5A+B
2A
2A= 4
A=2
3A+B=16
B=10
A+B +C =12
C=0
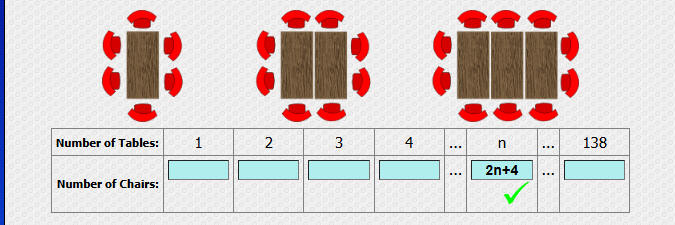
القاعدة
2n^2 +10 n
التأكد n=5
(50)+10(5) = 100
2n^2 +10 n
عامل مشترك
=
(2n(n+5
================================================================
الحل بالاستعانة بالشات
الفروق بين الأعداد المتالية هي
16 20 24 28 32




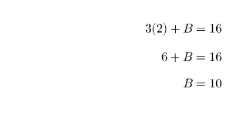



القاعدة العامة
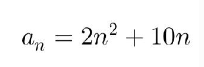
التأكد من الجدول السابق عدد الترتيبات =5 مجموع عدد الطاولات 100
2*5*5 + 10*5
100
الحل بطريقة الفروق
| الطاولات | مجموع الكراسي | الغرق 1 | الفرق 2 |
| 1 | 12 | 16 | 4 |
| 2 | 28 | ||
| 3 | 48 | 20 | |
| 4 | 72 | 24 | 4 |
| 5 | 100 | 28 | 4 |
| 6 | 132 | ||
| n | |||
الفرق الثاني هو الثابت معنى ذلك المعادلة من الدرجة الثانية
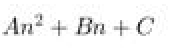
نعوض في المقدار n تساوي واحد و اثنين وثلاثة
A+B+C 4A+2B+C 9A+3B+C
نحسب الفرق 1
3A+B 5A+B
نحسب الفرق 2
2A
وعليه يكون
2A= 4
A=2
نعوض في المقدار
3A+B=16
نحسب B
B=10
نعوض في المقدار
A+B+C=12
C=0
المقدار
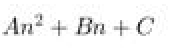
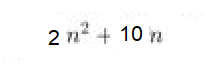
==================================================================
ويمكن استخدام آلة حاسبة نظم المعادلات في ايجاد المتغيرات
كما يمكن إدخال المعادلات في الشات وطلب ايجاد قيمة
A, B, C
بكتابة هذه المعادلاات نحصل على قيمة المتغيرات
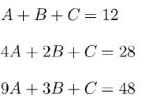
رابط حاسبة حل نظم المعادرت
Systems of Equations Solver: Step-by-Step Solutions - Wolfram|Alpha (wolframalpha.com)

واجهة البرمجية جاهزة لحل نظام من 4 معادلات
اختر عدد المعادلات من

ادخل المعادلات
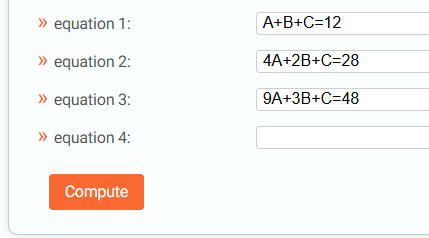
بعد كتابة المعادلات نضغط على زر

الحل

المقدار
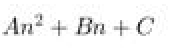
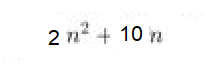
============================================================================
كما يمكن ادخال المعادلات في الشات مباشرة
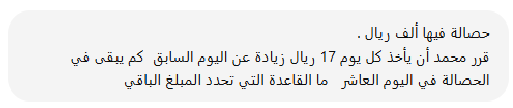
نشاط
حصالة فيه ألف ريال قرر محمد أن يأخذ كل يوم 17 ريال زيادة عن اليوم السابق فكم يبقى في الحصالة
بعد سحب اليوم العشر؟
ما القاعدة التي تحدد المبلغ الباقي؟
الحالة الأولى يكون فيها مقدار السحب الأول = الزيادة اليومية
حل شات جي بي تي
نكتب المسألة
المقدار الأول 17 والزيادة اليومية نفس المبلغ



|
قانون مجموع الأعداد المتتالية بصفة عامة إذا كان المبلغ المسحوب في أول مرة يساوي مبلغ الزيادة اليومية فإن مجموع المبلغ المسحوب لعدد محدد من الأيام تحكمه هذه الصيغة
n = عدد الأيام |
الحل بطريقة المتتاليات
يمكن بناء جدول يربط رقم اليوم والمبلغ
المبلغ الأساس 1000 ريال
من هذا الجدول
| اليوم | المبلغ | المبلغ | ||
| 1 | 17 | 1 | في | 17 |
| 2 | 34 | 2 | في | 34 |
| 3 | 51 | 3 | في | 51 |
| 4 | 68 | 4 | في | 68 |
| 5 | 85 | 5 | في | 85 |
| 6 | 102 | 6 | في | 102 |
| 7 | 119 | 7 | في | 119 |
| 8 | 136 | 8 | في | 136 |
| 9 | 153 | 9 | في | 153 |
| 10 | 170 | 10 | في | 170 |
القاعدة التي تربط المبلغ ليوم محدد هي رقم اليوم ضرب 17
| اليوم | المبلغ | الجموع |
| 1 | 17 | 17 |
| 2 | 34 | 51 |
| 3 | 51 | 102 |
| 4 | 68 | 170 |
| 5 | 85 | 255 |
| 6 | 102 | 357 |
| 7 | 119 | 476 |
| 8 | 136 | 612 |
| 9 | 153 | 765 |
| 10 | 170 | 935 |
| الباقي | 65 | |
الحد الأول = 17
الحد الأخير =170
عدد الأيام= 10
القاعدة
المجموع يساوي
نصف عدد الأيام ( الأول +الأخير)
5(17+170) = 5 (187)= 935
الباقي في الحصالة 1000 ناقص 935
65 ريال
|
قانون مجموع متتالية بصفة عامة إذا كان المبلغ المسحوب في أول مرة يساوي مبلغ الزيادة اليومية فإن مجموع المبلغ المسحوب في عدد محدد من الأيام تحكمه هذه الصيغة ( نصف عدد الأيام ) ( الحد الأول + الحد الأخير )
|
مثال :
المبلغ الموجود في الحصالة 4300 ريال اول يوم سحب 20 ريال واليوم التالي 20 زيادة عن اليوم السابق واليوم الثالث يسحب 60 ريال وهكذا لمدة 20 يوم
مجموع المبلغ المسحوب لعدد محدد من الأيام تحكمه هذه الصيغة
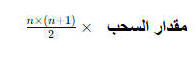
|
قانون مجموع الأعداد المتتالية بصفة عامة إذا كان المبلغ المسحوب في أول مرة يساوي مبلغ الزيادة اليومية فإن مجموع المبلغ المسحوب في عدد محدد من الأيام تحكمه هذه الصيغة
n = عدد الأيام
|
مجموع المبالغ المسحوبة في 20 يوم
=
20(20) (21)/2= 4200 ريال
الباقي 100 ريال
===========================================
طريقة المتتاليات
عدد الأيام 20
اليوم الأول = 20
اليوم رقم 20 =400
المجموع
نصف عدد الأيام = 10
الأول + الأخير=420
المجموع= 420 ضرب 10= 4200
===============================================================================
ماذا لو اختلف المبلغ المسحوب عن الزيادة اليومية
مثال
المبلغ في الحصالة 500 ريال
المدة عشرة أيام
يسحب أول يوم 20 ريال والزيادة اليومية 5 عن اليوم الذي قبله
20 25 30 35 40 45 ....
| اليوم | المبلغ | الفرق | القاعدة ليوم محدد
|
| 1 | 20 | 5 | 5n+15 |
| 2 | 25 | ||
| 3 | 30 | 5 | |
| 4 | 35 | 5 | |
| 5 | 40 | 5 | |
| 6 | 45 | 5 | |
| 7 | 50 | 5 | |
| 8 | 55 | 5 | |
| 9 | 60 | 5 | |
| 10 | 65 | 5 | |
| الباقي | |||
القاعدة التي تحدد السحب في يوم محدد هي
5n+15
الحد الأول - الفرق =15
المجموع بطريقة مجموع الأعداد المتتالية
مجموع 5n
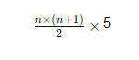
+
مجموع 15 لعدد الأيام
عدد الأيام =10
10x11x 5 /2 =275
+
مجموع 15 لعدد الأيام
150
275+150=425
التأكد
لحساب المجموع الكلي نبني جدول
| اليوم | المبلغ | المجموع | القاعدة
مجموع 5n+15
+ 150 |
| 1 | 20 | 20 | |
| 2 | 25 | 45 | |
| 3 | 30 | 75 | |
| 4 | 35 | 110 | |
| 5 | 40 | 150 | |
| 6 | 45 | 195 | |
| 7 | 50 | 245 |
10(11)5 /2= 275 + 150 = 425 |
| 8 | 55 | 300 | |
| 9 | 60 | 360 | |
| 10 | 65 | 425 | |
|
الباقي |
75 | ||
المجموع لعدد محدد من الأيام = مجموع المقدار

+
10(15)
يساوي
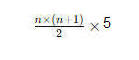 =
5(10)(11)/2=275
=
5(10)(11)/2=275
+
150
=425
الحل بطريقة المتتاليات
الحد الأول 20
المدة = 10
قانون الحدود
5n+15
الحد الأخير = 65
المجموع
نصف عدد الحدود =5
الأول + الأخير= 85
القانون
نصف عدد الحدود ( الأول + الأخير )
425= 5 85x
الهدف هوالوصول الى الحل بسرعة والتأكد من صحة الحل
التحدي يصنع الإبداع
نشاط 2
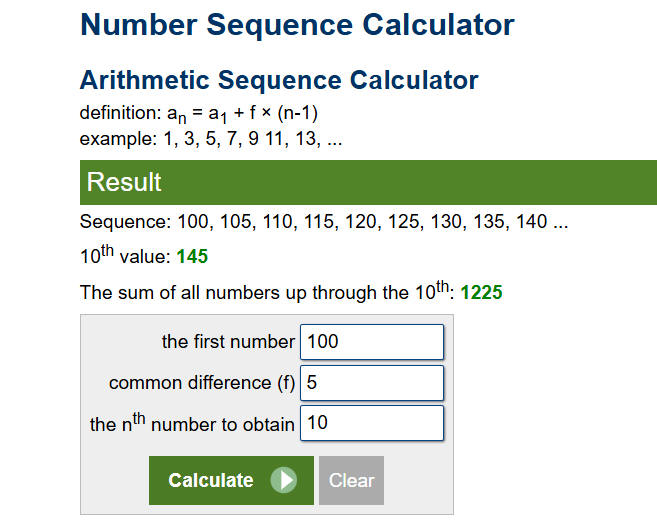
في هذا الشهرقرر محمد أن يضع 100 ريال في حصالته الشخصية , وأن يضع بعد ذلك كل شهر 5 ريال زيادة عن الشهرالذي قبله.
فكم المبلغ الذي يضعه في الشهر العاشر وما المبلغ الموجود في الحصالة بعد ايداعه الشهر العاشر ؟
| الشهر | المبلغ | الفرق | المجموع |
| الشهر الأول | 100 | 5 | 100 |
| الشهر الثاني | 105 | 205 | |
| الشهر الثالث | 110 | 5 | 315 |
| الشهر الرابع | 115 | 5 | 430 |
|
الشهر الخامس |
120 | 5 | 550 |
| الشهر السادس | 125 | 5 | 675 |
| الشهر السابع | 130 | 5 | 805 |
| الشهر الثامن | 135 | 5 | 940 |
| الشهر التاسع | 140 | 5 | 1080 |
| الشهر العاشر | 145 | 5 | 1225 |
| ---------- | ------- |
--------- |
|
|
--------- |
------ |
--------- |
طريقة أخرى :
100 105 110 115 120 ---- ----
يمكن تمثيل الوضع في صورة أزواج مرتبة
Y X 100 1 105 2 110 3 106 4 ------ ----- ------
------
------
الأزواج المرتبة تمثل خط مستقيم
معادلة الخط المستقيم
Y=ax+b
الميل = a
b =الجزء المقطوع من محور الصاات
الميل = 95
| Y | X |
| 100 | 1 |
الميل
y-x= 5
Y=5X+b
b=95
الحد النون 5x+95
Y=5X+95
اليوم العاشر يضع
145
=====================================================
الطريقة المعتادة
هذه الحالة تمثل متتالية حسابية حدها الأول 100 ومقدار الزيادة 5
الحد النوني
an = a + (n - 1)d
a= الحد الأول
d= الفرق الثابت
n= رتبة الحد
الحد العاشر
a10 = 100 + (10 - 1)5
145
| الشهر العاشر | 145 |

-----------------------------------------
لحساب المجموع نحسب مجموع الحد النوني
5x+95
مج 5x من واحد الى 10 وكذلك مج 95 عشر مرات
لمعرفة مجموع متتالية حسابية نستخدم القانون
البرمجية