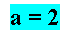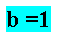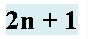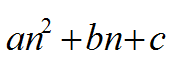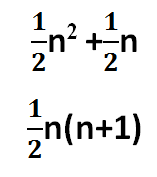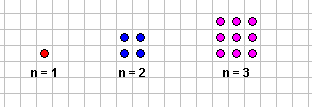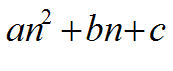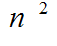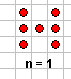|
تعلم التفكير |
|
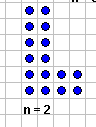
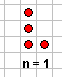
|||||||
|
|
|||||||||
المتتاليات
الهدف
اكتشاف قاعدة المتتالية
المستوى الأول
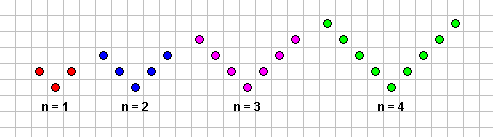
متتالية معطى بعض حدودها الأولى مثل الحد الأول والثاني والثالث والرابع..والمطلوب رسم شكل الحدالتالي ومعرفة القاعدة التي تحدد عدد النقاط في الحد ن ؟
يمكن الاستعانة بالبرمجية على الرابط
لرسم الحد الذي تريد
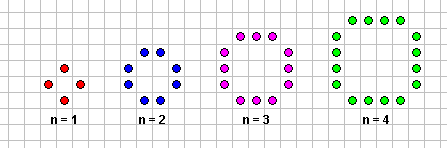
نشاط 1
الحل:
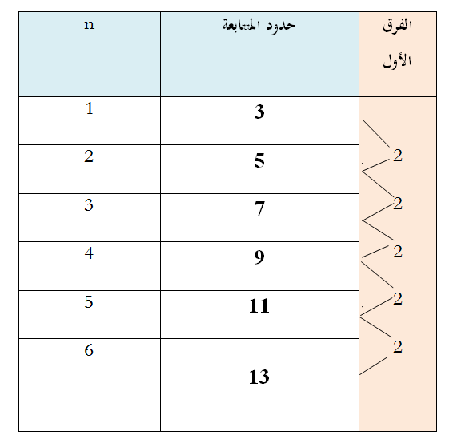
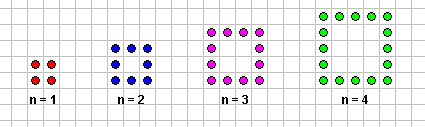
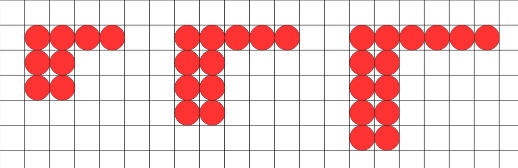
حدود المتتابعة التي تم الحصول عليها: 3 ، 5، 7 ، 9 ، 12 ، 13، ....أولاً: نكتب جدول الفروق:
لاحظ في المتتابعة أن الفروق ثبتت عند الفرق الأول لذا فالحد النوني للمتتابعة هو معادلة من الدرجة الأولى على الصورة an+b
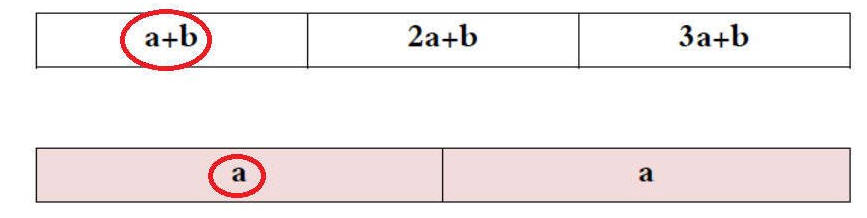
والآن لنوجد قيم a ، b بمطابقة جدول الفروق للمتتابعة مع جدول الفروق في هذه الحالة:
نعوض عن n في المقدار an+b مرة 1 ومرة 2 ومرة 3 كما يلي:
قيمة الفرق الثابت في المتتابعة المعطاة هي 2
قيمة الحد الأول من المتتابعة هو 3
a + b = 3
2 + b = 3
b = 3-2
إذن الحد النوني للمتتابعة هو :
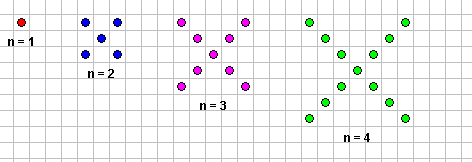
للوصول إلى القاعدة نقوم بمقارنة الأشكال وملاحظتها لمعرفة القاعدة التي تسير فيها هذه الأشكال
ومن الأفضل أن نسجل ملاحظاتنا في جدول :
الحد
عدد النقاط
الحد الأول
3
الحد الثاني
5
الحد الثالث
7
الحد الرابع
9
الترتيب (ن)
2ن+1
الإجابة صحيحة إذن قاعدة نمط هذا الشكل هي :
2ن+1
للتأكد نجرب على الحد الرابع
ن=4
2 ضرب 4 +1 = 9
وفي الكتب الدراسية قانون الحد النوني مرتبط برتبة الحد وفق القاعدة التالية
الحد النوني = الحد الأول +الفرق (رتبة الحد - 1)
الحد الرابع= الأول +2 (4-1)
الحد الرابع = 3+ 6=9
نشاط 2*****
=====================================================================================================================
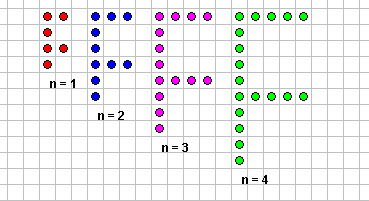
من خلال ملاحظتك للأشكال هل استطعت الوصول إلى قاعدة النمط ؟
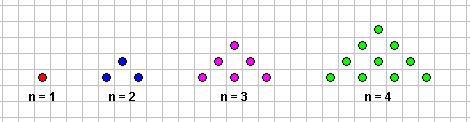
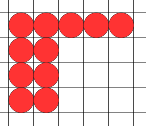
حدود المتتابعة التي يمثلها الشكل السابق 1 ، 3 ، 6، 10 ، 15
للوصول إلى القاعدة نقوم بمقارنة الأشكال وملاحظتها لمعرفة القاعدة التي تسير فيها هذه الأشكال
ومن الأفضل أن نسجل ملاحظاتنا في جدول :
الحد
عدد النقاط
الحد الأول
1
الحد الثاني
3
الحد الثالث
6
الحد الرابع
10
الترتيب (ن)
؟؟؟
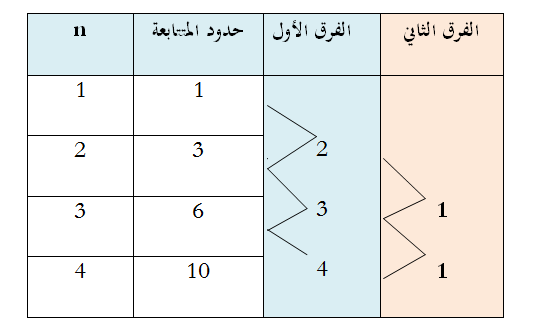
نلاحظ في المتتابعة أن الفروق ثبتت عند الفرق الأول لذا فالحد النوني للمتتابعة هو معادلة من الدرجة الأولى على الصورة an+b.
والآن لنوجد قيم a ، b بمطابقة جدول الفروق للمتتابعة مع جدول الفروق في هذه الحالة:
نلاحظ في المتتابعة أن الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هو معادلة الدرجة الثانية
والآن لنوجد قيم a , b , c بمطابقة جدول الفروق للمتتابعة مع جدول الفروق في هذه الحالة:
قيمة الفرق الثابت في المتتابعة المعطاة هي 1
2a = 1
a = 1/2
قيمة الحد الأول من الفرق الأول هي 2
3a + b =2
3 (1/2) + b = 2
3/2 + b = 2
b = 2 -(3/2)
b = 1/2
قيمة الحد الأول من المتتابعة هو1
a + b + c = 1
1/2 + 1/2 + c = 1
c =0
إذن الحد النوني للمتتابعة هو :
إذن قاعدة نمط هذا الشكل هي :
ن(ن+1)÷2
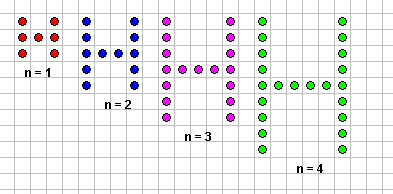
======================================================================================================================نشاط 3
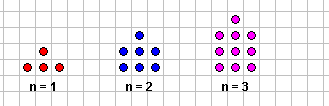
من خلال ملاحظتك للأشكال هل استطعت الوصول إلى قاعدة النمط ؟
للوصول إلى القاعدة نقوم بمقارنة الأشكال وملاحظتها لمعرفة القاعدة التي تسير فيها هذه الأشكال
ومن الأفضل أن نسجل ملاحظاتنا في جدول :
الحد
عدد النقاط
الحد الأول
1
الحد الثاني
4
الحد الثالث
9
الحد الرابع
16
الترتيب (ن)
ن2
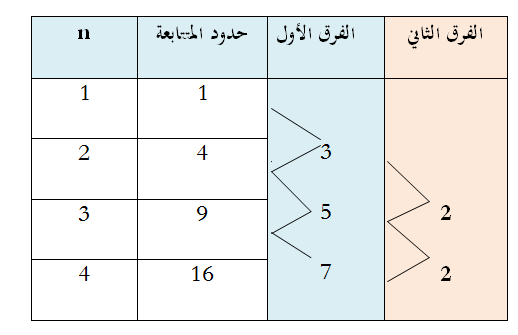
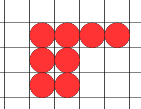
حدود المتتابعة التي يمثلها التشكيلان السابقان 1، 4 ، 9 ، 16، 25 ، 36
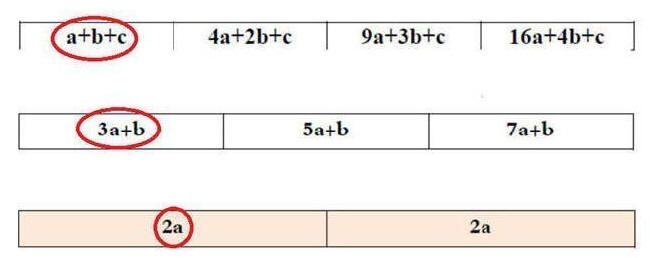
أولاً: نكتب جدول الفروق
نلاحظ في المتتابعة أن الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هو معادلة الدرجة الثانية
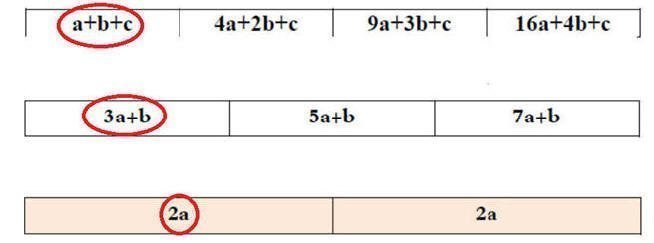
والآن لنوجد قيم a , b , c بمطابقة جدول الفروق للمتتابعة مع جدول الفروق في هذه الحالة:
قيمة الفرق الثابت في المتتابعة المعطاة هي 2
2a = 2
a = 1
قيمة الحد الأول من الفرق الأول هي 3
3a + b =3
3 (1) + b = 3
3 + b = 3
b = 0
قيمة الحد الأول من المتتابعة هو 1
a + b + c = 1
1 + 0 + c = 1
c =0
إذن الحد النوني للمتتابعة هو :
وهي متتابعة الأعداد المربعة
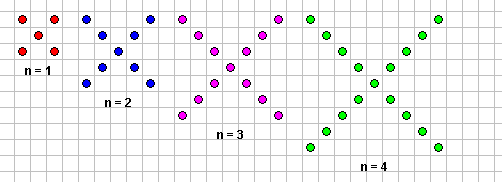
نشاط 4
نشاط 5
نشاط6
نشاط7
نشاط8
نشاط9
نشاط10
نشاط11
نشاط12
نشاط13
نشاط14
استخدم البرمجة المساعدة لبناء نظام من تصميمك واكتب قاعدة النظام الذي كونته
البرمجية المساعدة
رابط البرمجية المساعدة
نشاط15
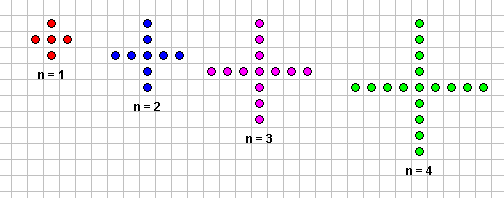
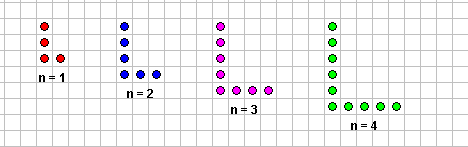
استخدم البرمجية المساعدة لتصميم المتتالية التالية واحسب قاعدة المتتالية
الحد
عدد النقاط
الحد الأول
8
الحد الثاني
11
الحد الثالث
14
الحد الرابع
17
الحد الخامس
الحد السادس ن
الحدود 8 11 14 17
الفرق 3
الحد النوني
3ن + ؟ = الحد الأول
3ن +؟ = 8
الحد النوني = 3ن + 5
التأكد
الحد الرابع ن=4
17
طريقة حساب الحد النوني متتابعة حسابية في كتب الرياضيات :
في المتتاليات الحسابية
an
رمز الحد النوني
—————————————
d
رمز الفرق بين حدين متتاليين
—————————————-
n
رمز عدد حدود المتتالية
——————————————
a1
رمز الحد الأول في المتتالية
—————————————
Sn
رمز مجموع متوالية حسابية
—————————————
الحد النوني للمتتالية
(an= a1 +d(n-1
الحد النوني = الحد الأول + الفرق( رتبة الحد - 1 )
——————————————-
التأكد
الحد الأول = 8
الحد الرابع = 17
الفرق = 3
الحد النوني = الحد الأول + الفرق( رتبة الحد - 1 )
الحد الرابع = 8 + 3( 4- 1 )
الحد الرابع = 8+9= 17
لحساب مجموع عدد محدد من حدود متتالة حسابية نستخدم الفانون التالي :
مجموع عدد من حدود متتالية
Sn = نصف عدد الحدود ( an+a1)
——————————————
كما يمكن معرفة مجموع المتتالية السابقة بطريقة الفروق السابق استخدامها
مثال ماقاعدة مجموع حدود المتتالية
| الحد النوني | الحد الخامس | الحد الرابع | الحد الثالث | الحد الثاني | الحد الأول |
|
|
|
|
|
||
|
17 |
14 | 11 | 8 |
|
الحد |
عدد النقاط |
مجموع النقاط |
|
الحد الأول |
8 |
8 |
|
الحد الثاني |
11 |
19 |
|
الحد الثالث |
14 |
33 |
|
الحد الرابع |
17 |
50 |
|
الحد الخامس |
20 |
70 |
|
الحد السادس |
||
|
ن |
3n+5 |
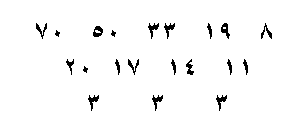
الفرق اصبح ثابت في المرة الثانية نكمل بالطريقة نفسها
أو نحسب مجموع الحد النوني
مجموع 3n
+
مجموع 5
أو بالطريقة المتبعة في الكتب
Sn = نصف عدد الحدود ( an+a1)
على سبيل المثال مجموع الأربع حدود في المتتالية السابقة
عدد الحدود =4
الحد الأول =8
الحد الرابع=17
المجموع = 2 ( 17 + 8) =25