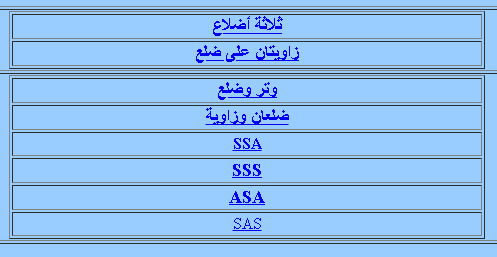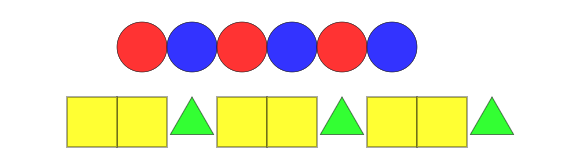
الأنماط
البرمجية
أنماط بسيطة

برمجية انماط متقدمة
أشكال الأنماط الرياضية (aghandoura.com)
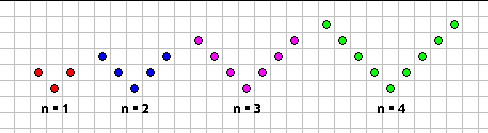
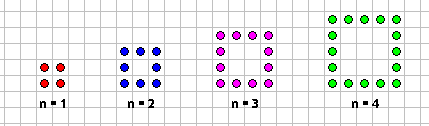
اللوحة الهندسية
https://apps.mathlearningcenter.org/geoboard/

الأشكال الهندسية ومساحتها
ما اسم الشكل الأيمن ؟
احسب مساحته ؟
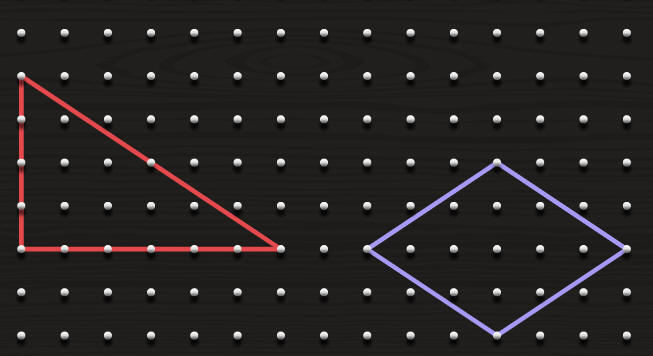

https://aghandoura.com/SINGAMATH/99f.html
 |
|
الاعداد الزوجية والأعداد الفردية
https://aghandoura.com/NF/FRAME/N%20Frames.html
============================================================================================
معنى المحيط
https://aghandoura.com/rectangle.html
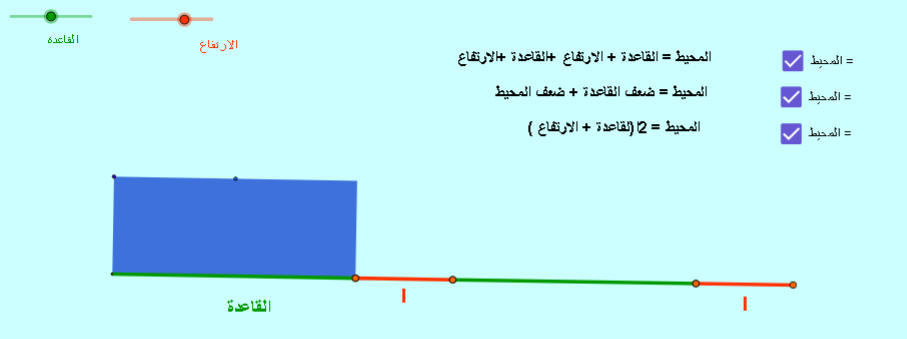
المساحة
https://aghandoura.com/GEOMETRY/TABLE1.htm
المساحة والمحيط
https://aghandoura.com/2030/APPLETS/Area%20Perimeter.htm
قارن بين مساحتي الشكلين 1 و2
قارن بين محيطي الشكلين 1 و2
|
|
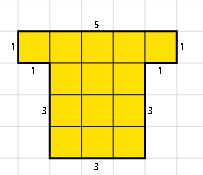 |
| شكل 1 | شكل 2 |
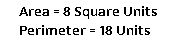 |
|
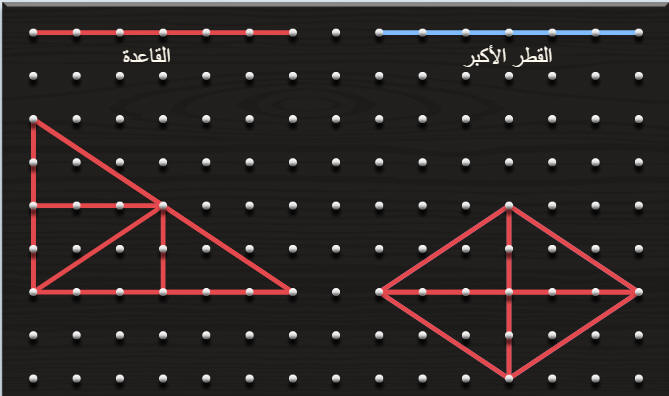
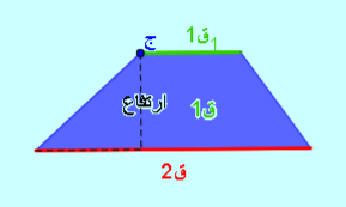
مساحة شبه المنحرف مقارنة بمساحة مثلث
https://aghandoura.com/A/mNR6gkNck-Area-of-a-Trapezoid-Discovery.html
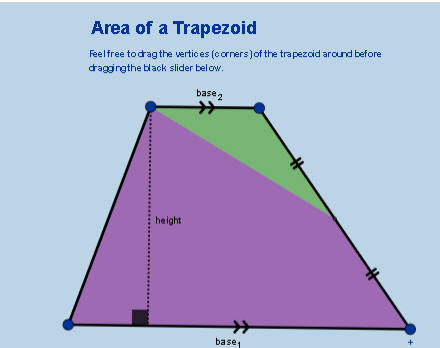
base1= القاعدة الكبرى
base2=القاعدة الصغرى
تحويل الشكل الى مثلث
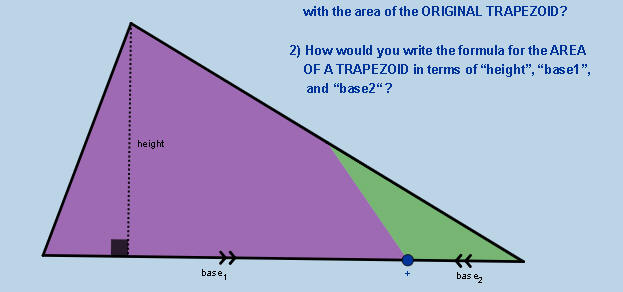
مساحة المثلث = نصف (القاعدة الكبرى + القاعدة الصغرى ) ضرب الارتفاع
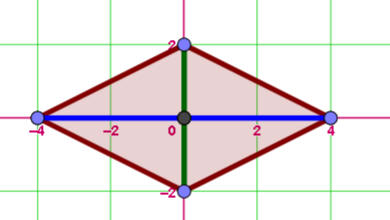
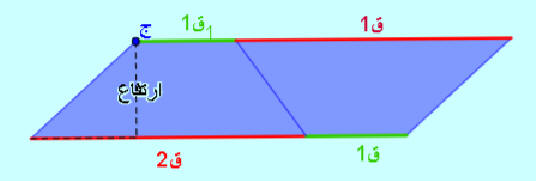
مساحة المعين مقارنة بمساحة مستطيل
برمجية
https://aghandoura.com/A/RAM1.html
ربط مساحة المعين بمساحة المستطيل
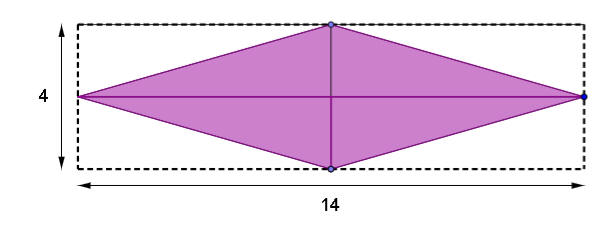
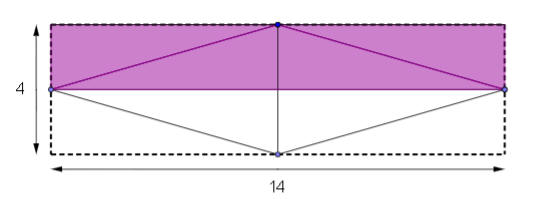
طريقة أخرى
https://aghandoura.com/GEOMETRY/16.html
 |
 |
محيط الدائرة
https://www.aghandoura.com/geogebra/TATBEEK/CIRKL/18.html
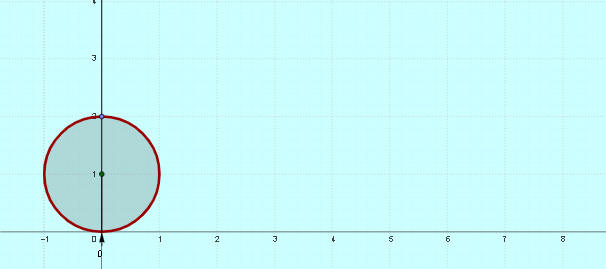
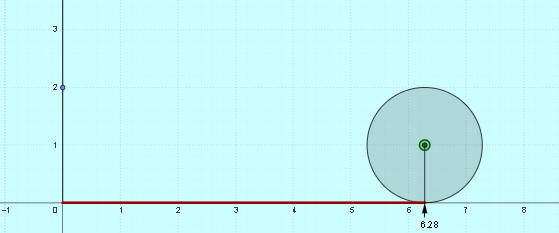
برمجية محيط الدائرة ومساحتها
https://aghandoura.com/A1/HANAN/APPLET/G2-65.html
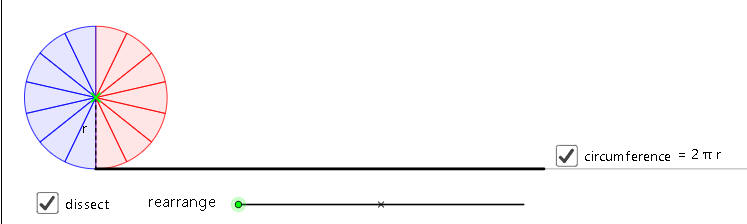
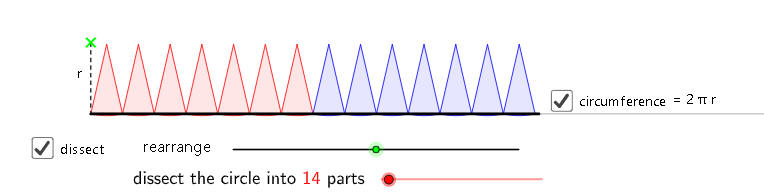
مساحة الدائرة
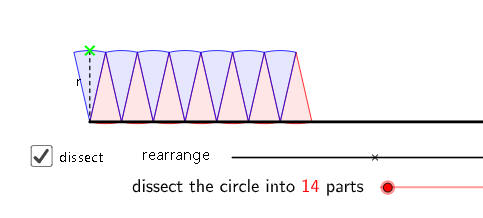
=========
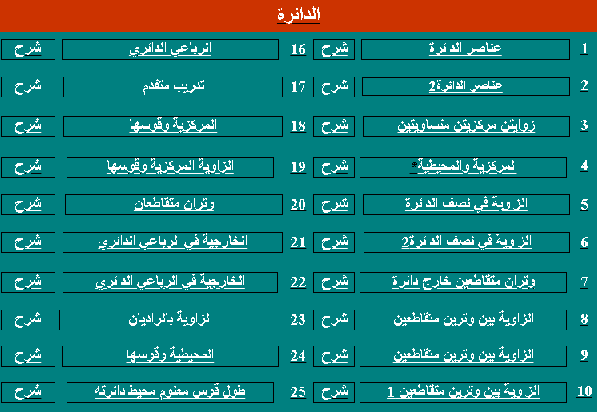
نظريات الدائرة
https://www.aghandoura.com/geogebra/TATBEEK/CIRKL/CIRKL.htm
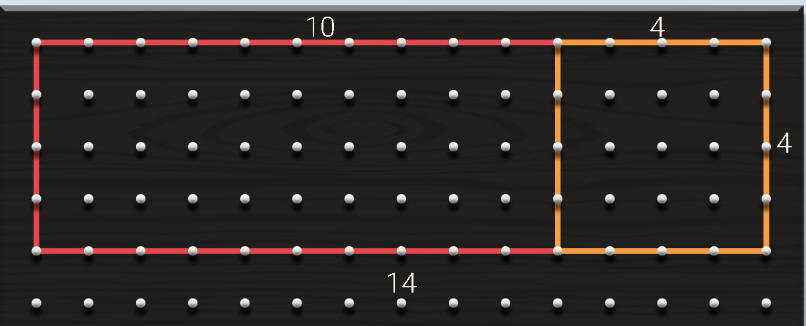
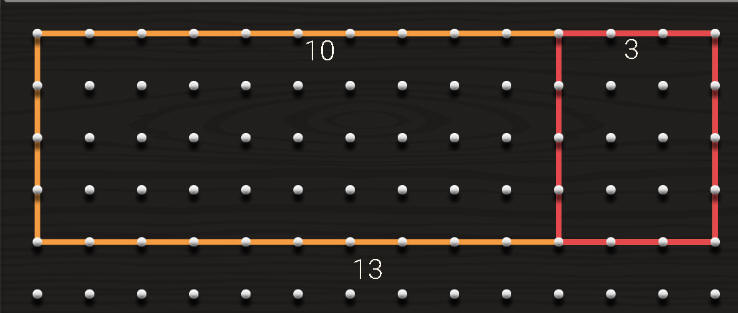
ضرب 14 في 4
يتم تقسيم العدد المكون من رقمين الى 10 +الباقي
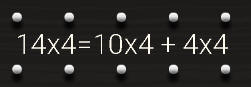
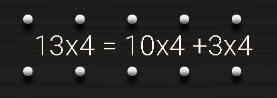
قواسم العدد
مثال لمعرفة قواسم العدد 18 نبني مستطيلات حاصل ضرب بعدي كل مستطيل =18
ما العددان اللذين حاصل ضربهما = 18
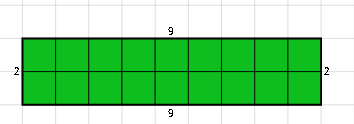 |
1 و 18
|
|
1 و 18
2 و 9
3 و6
| قواسم العدد 18 | |||||
| 1 | 2 | 3 | 6 | 9 | 18 |
مثال لمعرفة قواسم العدد 24 نبني مستطيلات حاصل ضرب بعدي كل مستطيل =24
1و 24
2و12
3و8
4و6
| قواسم العدد24 | |||||||
| 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
لمعرفة القاسم المشترك الأكبر للعددين 18 و 24
| القاسمالمشترك الأكبر للعددين 18 و 24 | |||||||
| 1 | 2 | 3 | 6 | 9 | 18 | ||
| 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
القاسم المشترك الأكبر 6
مضاعفات العدد 18
| مضاعفات العدد18 | |||||||
| 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
| 18 | 36 | 54 | 72 | ||||
| مضاعفات العدد24 | |||||||
| 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
| 24 | 48 | 72 | |||||
نجد أن المضاعف المشترك الأصغر للعدين 18 و 24 هو72
برمجية للعمليات على الكسور
https://aghandoura.com/2030/APPLETS/Fraction%20Grids.html
| الواحد | الثلث | الربع | المجموع |
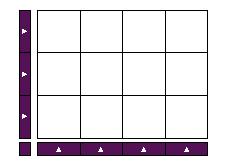 |
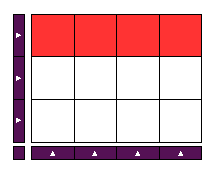 |
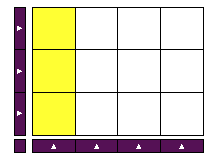 |
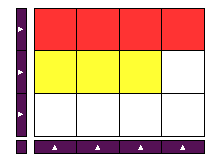 |
بالطريقة نفسها ممكن نمثل الطرح والقسمة
تطبيقات على الكسور
https://www.aghandoura.com/FRACTIONS2020/FRACTIONS2020.htm

متطابقة مربع مجموع حدين
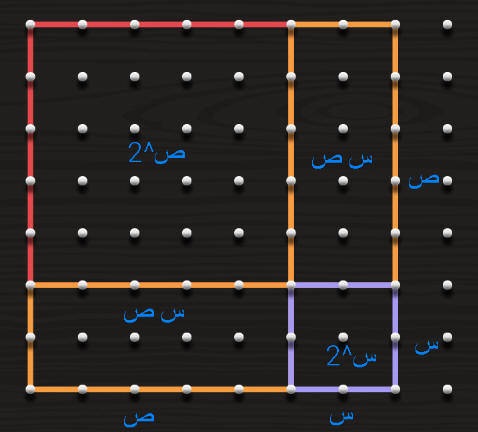
برمجية
https://aghandoura.com/2030/APPLETS/Algebra%20Tilesboth.htm
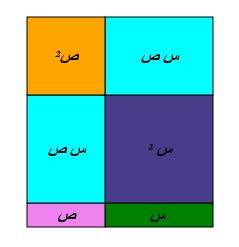
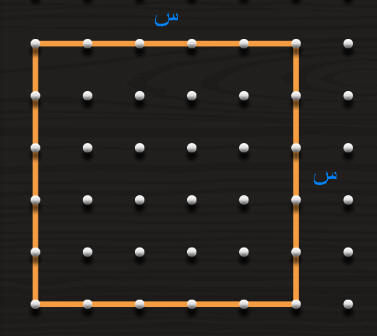
مساحة المربع الكبير = س تربيع
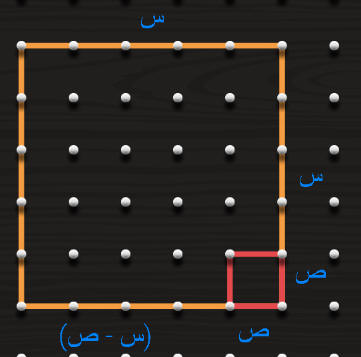
مساحة المربع الصغير = ص تربيع
س تربيع ناقص ص تربيع
متطابقة الفرق بين مربعين
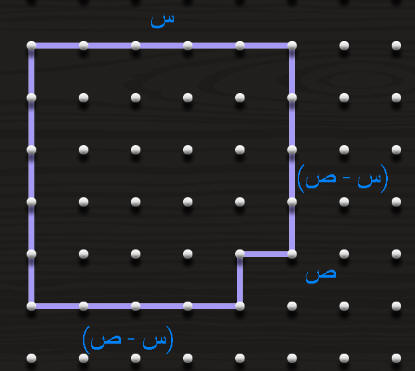
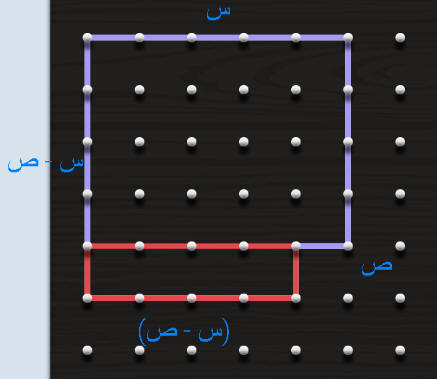
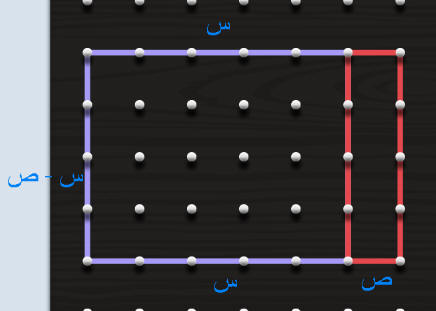

نظرية فيثاغورث
https://aghandoura.com/2030/APPLETS/GeoboardNEW.htm
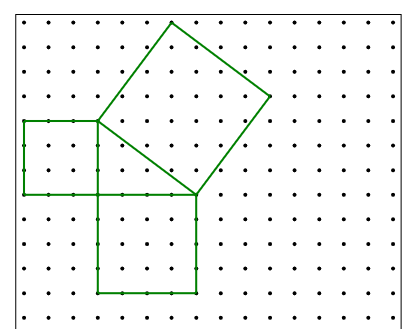
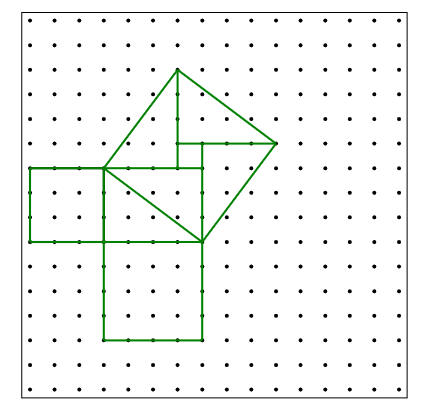
نظرية طالس
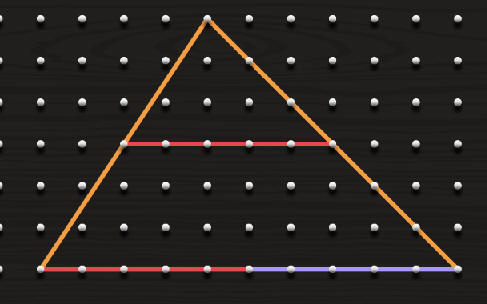
نظرية
القطعة المستقيمة من رأس الزاوية القائمة الى منتصف الوتر = نصف طول الوتر
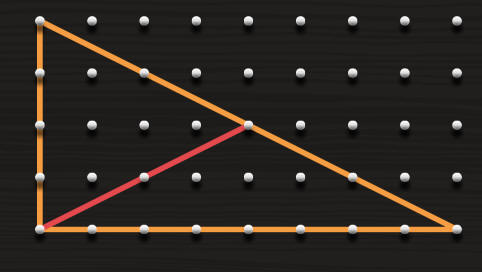
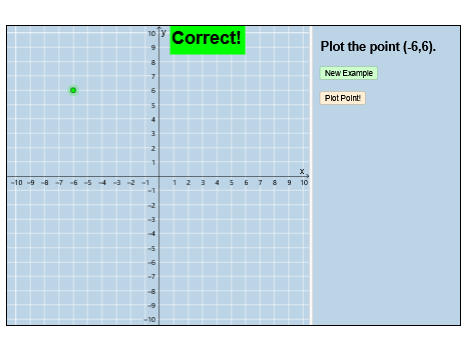
احداثيات نقطة
البرمجية
https://aghandoura.com/A1/hayfa/applet/mW8hHuY7N-Plotting-Points-xy-Dynamic-Illustration.html
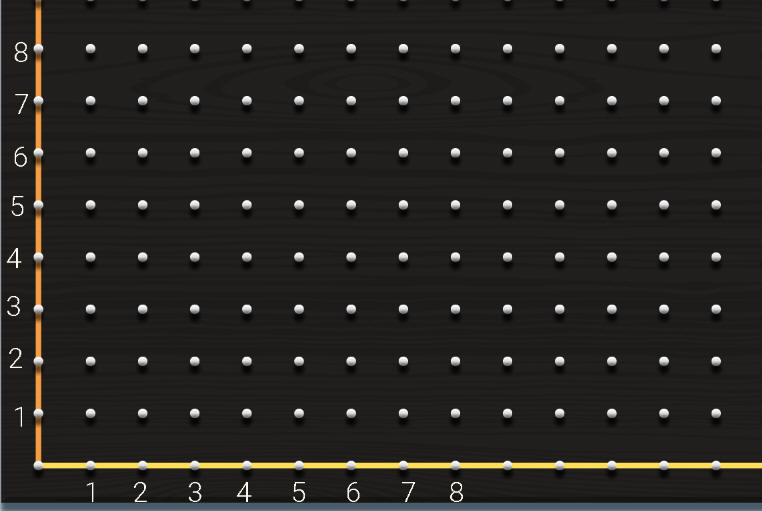
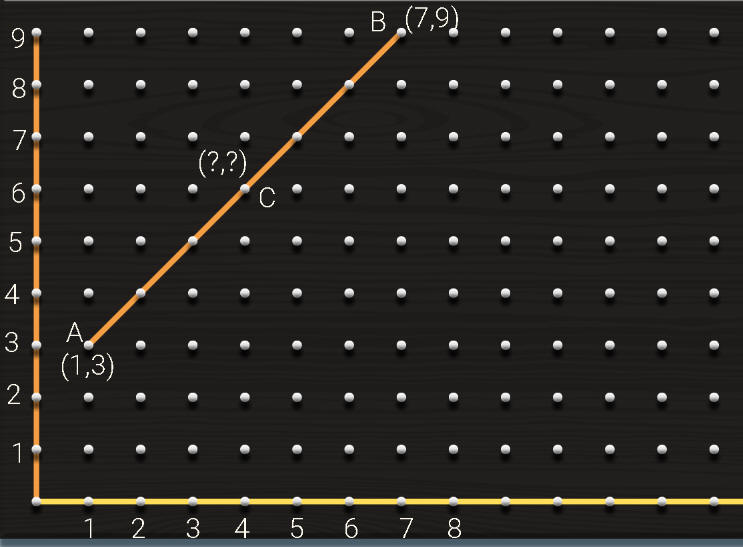
ما احداثيات C
ما ميل AB
برمجية
https://www.aghandoura.com/geogebra/TATBEEK/LINEEQUATION/2.html
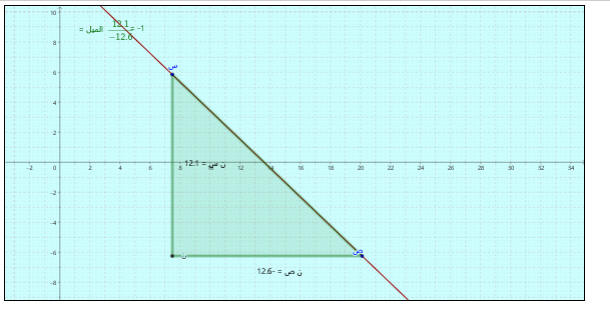
https://aghandoura.com/SIGMA/PP/LE.html
ما معادلة AB
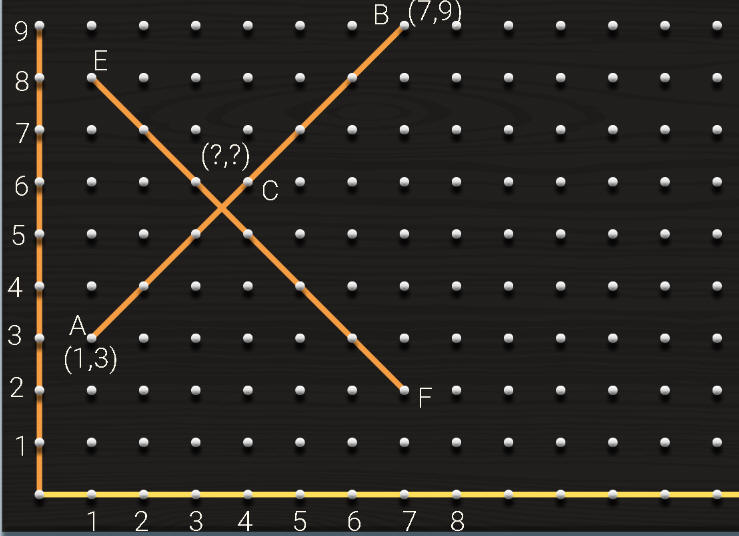
هل المستقيمان متعامدان
ما معادلة EF
احسب ميل كل منهما ماذا تلاحظ
البرمجية
https://www.aghandoura.com/geogebra/TATBEEK/LINEEQUATION/9.html
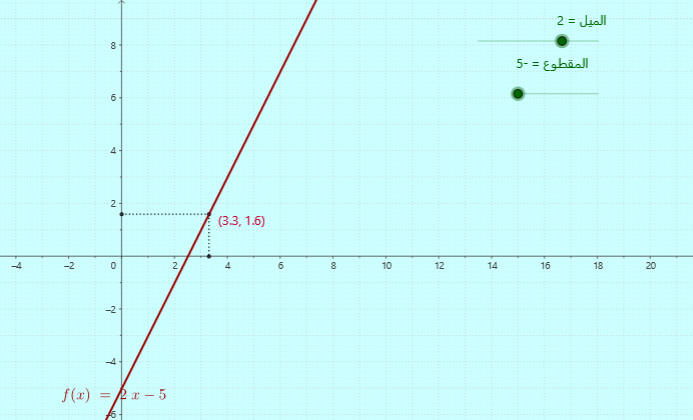
حل المعادلتين
ما علاقة الحل باحداثيات نقطة التقاطع
حل نظام معادلتين بيانيا
https://aghandoura.com/SITE/SSYSTEM.htm
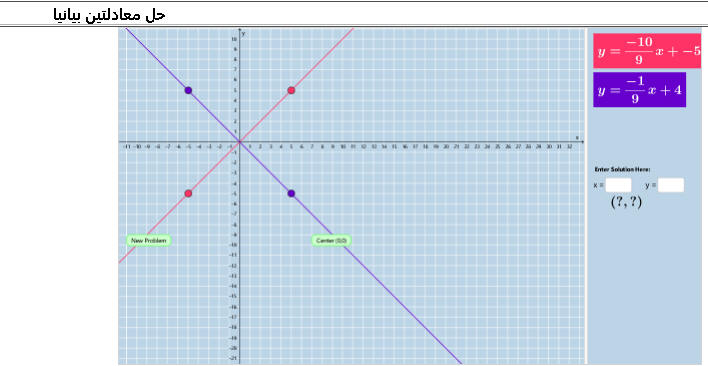
-------------------------------------------------------------
التناظر حول محور

التناظر حول نقطة
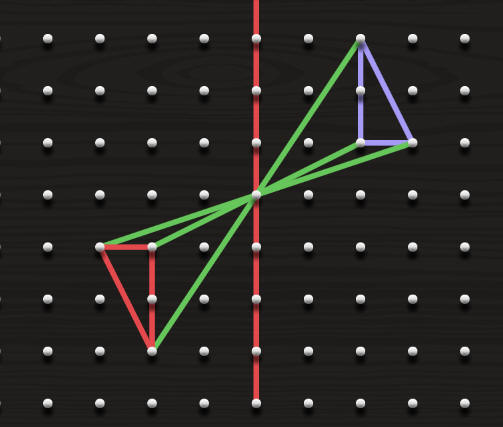
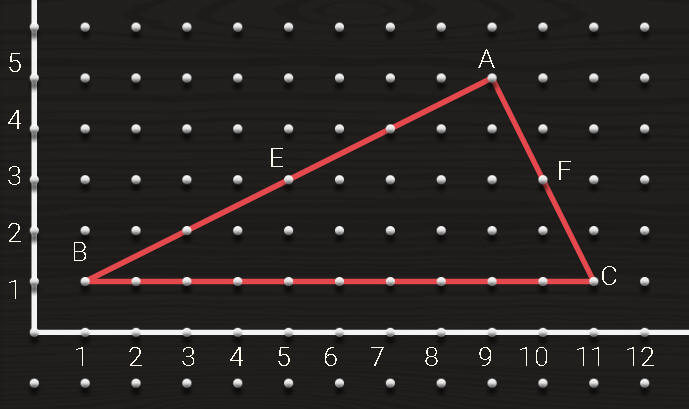
اثبت بثلاث طرق مختلفة أن المثلث قائم الزاوية
احسب
1- مساحة المثلثABC
2- طول AB
3- احداثيات رؤوس المثلث
4- احداثيات E , F
5- ميل AB و ميل AC ما العلاقة بين الميلين
6- معادلة AB
7- معادلة AC
تطابق المثلثات
https://aghandoura.com/NEWBOOKS/8%201/5/4/applet.htm