القسمة:

يمكن استخدام الميزان المطور في دراسة العديد من مسائل القسمة حتى يدرك الطالب معنى القسمة بطريقة مسحنة ملموسة قبل تقديم الخوارزميات التي تتم بها عملية القسمة،

ومن الممكن للطالب أن يستنتج الخوارزمية إذا أتيحت له فرصة الممارسة على الميزان وحل المسائل به.

فعملية قسمة 1 +   = □

يمكن ترجمتها بالسؤال التالي: كم نصف يوجد في الواحد الصحيح؟ أو الواحد صحيح كم نصف يحتوي؟

تم تمثيل المقسوم عليه "النصف" بوضع ثقل على المشجب الذي يمثل النصف ثم وضع أثقال على ذلك المشجب " الذي يمثل المقسوم عليه" من الذراع الأيسر حتى يتعادل ذراعا الميزان.

وفي هذه الحالة يعادل الميزان بوضع ثقلين اثنين على المشجب الذي يمثل المقسوم عليه مما يعني أن خارج القسمة هو اثنين.

والشكل التالي يوضح الفكرة

وبالطريقة نفسها يمكن تمثيل عملية قسمة:

  1 ÷  = □

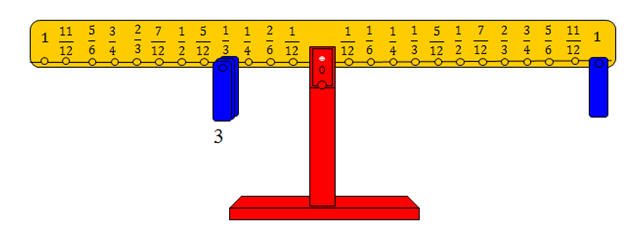
بوضع ثقل واحد على المشجب الذي يمثل المقسوم وثقل على المشجب الذي يمثل المقسوم عليه ثم وضع أثقال على المشجب الذي يمثل المقسوم عليه حتى يعود الميزان إلى حالة التعادل

وفي هذه الحالة احتجنا إلى 3 أثقال مما يعني أن : □ = 3 .

وبتكرار النشاط الأخير يمكن حل المعادلات التالية:

1 ÷  = □

1 ÷  = □

ووضع قاعدة عامة لقسمة الواحد صحيح على (كسر الوحدة) يكون خارج القسمة يساوي مقام كسر الوحدة أي: 1 ÷  = □

أما قسمة عدد صحيح على كسر الوحدة الذي مقامه يساوي العدد الصحيح مثل قسمة:

2 ÷  = □

فإن السؤال المطروح هو أن الاثنين تحتوي على كم نصف؟ أو كم نصف موجود في العدد اثنين؟

ويمكن تمثيل جميع المسائل التي من هذا النوع على النحو التالي:

·       تمثيل المقسوم على الذراع الأيمن بوضع أثقال على المشجب الذي يمثل الوحدة وفي هذه الحالة نشع ثقلين اثنين على ذلك المشجب من الذراع الأيمن.

والشكل التالي يوضح الفكرة

وبالطريقة نفسها يمكن حل المعادلة: 3 ÷  = □

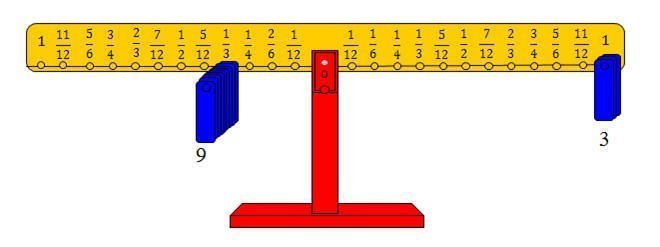
حيث يتم وضع 3 أثقال على المشجب الذي يمثل الواحد من الذراع الأيمن.

وبصورة عامة فإن

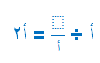
أما المعادلات التي من النوع  □ ÷  = 4

فيمكن تمثيلها على النحو التالي:

تمثيل خارج القسمة على الذراع الأيسر من الميزان وفي هذه الحالة نضع أربعة أثقال على المشجب الذي يمثل الواحد.

وضع عدد من الأثقال على المشجب الذي يمثل المقسوم عليه (وهو النصف في هذه الحالة) على الذراع الأيمن من الميزان.

وضع عدد الأثقال على ذلك المشجب الذي يعيد التوازن هو المقسوم.

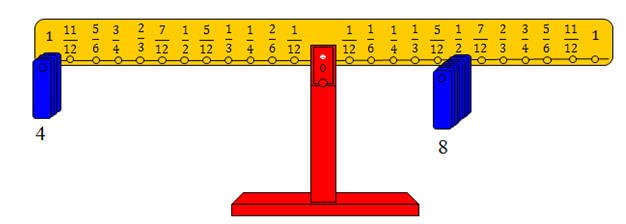
حيث تم وضع 8 أثقال على المشجب الذي يمثل النصف من الذراع الأيمن . وعليه فإن :

□ = 8

وبالطريقة يمكن حل المعادلة: □ ÷  = 2

حيث تم تمثيل خارج القسمة (2) على الذراع الأيسر من الميزان بوضع ثقلين اثنين على المشجب الذي يمثل الواحد، ووضع أثقال على المشجب الذي يمثل المقسوم عليه ( ) من الذراع الأيمن.

وحيث إن عدد الأثقال على ذلك المشجب هو 6  فإن المقسوم يساوي 6 ،  أي أن : □ = 6

والمعادلة السابقة يمكن أن تكون في صورة سؤال مثل:

كم ثلثاً موجودة في الاثنين؟ أو : الاثنين فيها كم ثلث؟

وحيث إن الواحد يحتوي على ثلاثة أثلاث، فإن الاثنين تحتوي على ستة أثلاث.

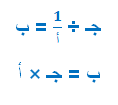
وهذا يعطي للطالب معنى محسوس لخوارزمية القسمة عندما نقول له حول إشارة القسمة إلى ضرب ثم اقلب الكسر أي اجعل المقام بسطاً، واجعل البسط مقاماً ثم أتمم عملية الضرب.

أما عملية قسمة 4÷  = □

فيمكن ترجمتها إلى السؤال التالي:

الأربعة فيها كم ثلثين؟ أو : كم ثلثين موجودة في الأربعة؟

ويمكن في البداية البدء بأشياء محسوسة مثل أصابع اليد، فأصابع اليد ما عدا الإبهام مكونة من أجزاء ثلاثة في كل اصبع، ويمكن اعتبار الجزء الواحد يمثل الثلث

 (مع ملاحظة أن الأثلاث في هذه الحالة غير متساوية). وهكذا يدرك الطالب أن الأربعة أصابع فيها ستة أجزاء ، وكل جزء يمثل الثلثين.

أو يمكن استخدام 4 مربعات متساوية يتم تقسيم كل منها إلى أثلاث على النحو التالي:

فنحصل على أربعة أجزاء مظللة، وكل جزء يمثل ثلثين. والثلث غير المظلل من المربع الأول مع الثلث غير المظلل من المربع الثاني يمثلان ثلثين،

 وهكذا نكون قد حصلنا على خمسة قطع، كل قطعة تمثل ثلثين. وبالطريقة نفسها نضع الثلث غير المظلل من المربع الثالث مع الجزء غير المظلل من المربع الرابع ليشكلا ثلثين،

وهكذا نكون قد حصلنا على ستة قطع من كل قطعة تمثل ثلثين، أي أن الأربعة فيها ستة قطع من النوع ثلثين

ويمكن بعد ذلك الانتقال إلى الميزان وتمثيل المعادلة:

4 ÷  = □

حتى يحصل التعادل. وحيث إنه قد تم وضع ستة أثقال على ذلك المشجب فإن: □ = 6

 والشكل التالي يوضح الفكرة

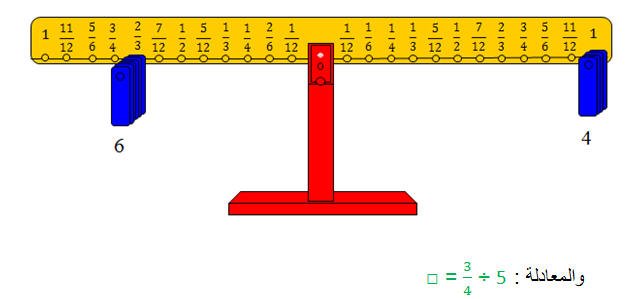
يمكن ترجمتها إلى السؤال التالي:

كم ثلاثة أرباع في الخمسة؟

ونظلل الجزء الذي يمثل  من كل مربع على النحو التالوهكذا حصلنا على خمس قطع كل قطعة منها يساوي  .

كما يمكن الحصول على قطعة سادسة تمثل  من المربعات الثلاثة الأولى مما يعني أننا حتى الآن حصلنا على ست قطع.

وحيث إن القطعة الواحدة فيها ثلاثة أجزاء من هذا النوع، فإن معنى ذلك أن القطعتين المتبقيتين لا تمثلان الواحد وإنما ثلثي هذه القطعة.

وعليه فإن □ =  

والشكل التالي يوضح الحل بالميزان

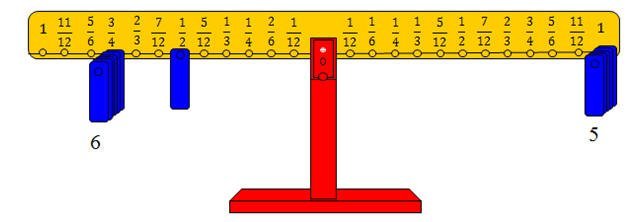
حيث تم تمثيل المقسوم (5) بوضع خمسة أثقال على المشجب الذي يمثل الواحد من الذراع الأيمن. ثم وضع أثقال على المشجب الذي يمثل  من الطرف الأيسر.

 وحيث إن ستة أثقال لا تكفي لإعادة التوازن، وأن سبعة أثقال على ذلك المشجب تكون أكبر من اللازم، فإن معنى ذلك أننا نكتفي بوضع ستة أثقال والبحث عن المشجب الذي يعيد التوازن

وبعد البحث نجد أنه المشجب الذي يمثل النصف

مما يعني أن : □ =  

حيث يتم تمثيل المقوسم (6) بوضع ستة أثقال على المشجب الذي يمثل الواحد من الذراع الأيمن وتمثيل المقسوم عليه  بوضع ثقل على المشجب الذي يمثل النصف

 وثقل على المشجب الذي يمثل الواحد على الذراع الأيسر. ووضع أثقال على هذين المشجبين بالتناوب غلى أن يحدث التوازن. وعدد الأوزان على أي منهما يمثل خارج القسمة.

كما في الشكل التالي

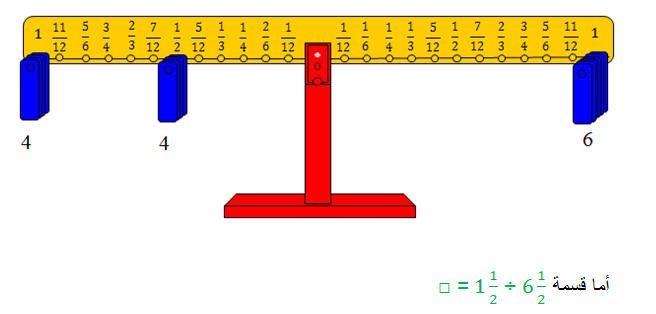
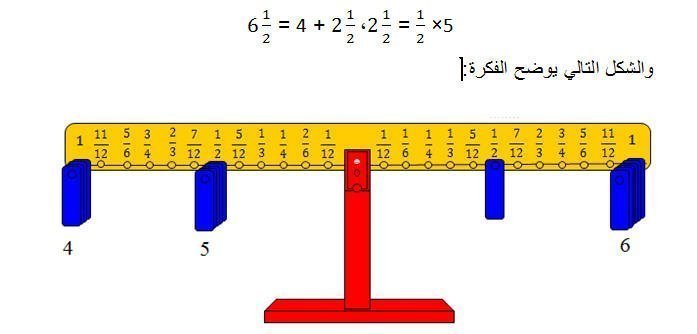
فيمكن ترجمتها إلى السؤال التالي: كم واحد ونصف موجود في الستة والنصف؟ أو الستة والنصف فيها كم واحد ونصف؟

ويمكن استخدام الميزان للإجابة عن السؤال باتباع الخطوات التالية:

تمثيل المقسوم  بوضع ثقل على المشجب الذي يمثل النصف وستة أثقال على المشجب الذي يمثل الواحد من الذراع الأيمن، وعلى الذراع الأيسر يتم تمثيل المقسوم عليه ( )

بوضع ثقل على المشجب الذي يمثل النصف، وآخر على المشجب الذي يمثل الواحد من الذراع الأيسر. ثم نصع أثقالاً على كل من المشجبين بالتناوب لحين حدوث التوازن. وحيث إن أربعة أثقال

على كل منهما لا تعيد التوازن، وأن نخمسة أثقال على كل منهما أكبر من اللازم، فإن معنى ذلك أننا بحاجة إلى أربعة أثقال على كلا المشجبين، والبحث عن مشجب ثالث لإعادة التوازن،

وبالبحث نجد أنه المشجب الذي يمثل النصف. وعليه فإن □ =

لأن  في هذه الحالة هي التي تمثل الوحدة. ولذلك يصبح لدينا خمسة أثقال على المشجب الذي يمثل النصف (ثلث الواحد والنصف).

ويمكن استخدام شرائح الكسور أو قطع النماذج في شرح وتوضيح الإجابة على العديد من مسائل القسمة.