الضرب:

 حيث يضع 3 أثقال على المشجب رقم  على الذراع الأيمن ويحاول إعادة التوازن بوضع أثقال على الذراع الأيسر فيجد أن ثقلاً واحداً أعاد التوازن. والشكل التالي يوضح الفكرة

والشكل التالي يوضح ذلك

وبصورة عامة فإن أ ×  = 1

أي أن:

ثم بعد ذلك يمثل عمليات ضرب عدد صحيح في كسر مقامه مغاير للعدد كأن يضرب:

4 ×  = □

حيث يضع أربعة أثقال على المشجب الذي يمثل الثلث من الذراع الأيمن ويحاول إعادة التوزان بوضع أثقال على مشجب من مشاجب الذراع الأيسر،

 وحيث إن ثقلاً واحداً لا يكفي لإعادة التوازن، مما يعني أن هناك حاجة إلى وضع ثقل آخر، وعند وضع ثقل ثاني على ذلك المشجب يميل الذراع نحو الأسفل دلالة على أن ثقلين أكبر من المطلوب.

وعند وضع ثقل واحد على المشجب رقم واحد ووضع ثقل آخر على المشجب الذي يمثل الثلث يحصل التوازن، أي أن :

وهذا معناه أن أربعة أثلاث تساوي واحد وثلث.

وبالطريقة نفسها يمكن إجراء عملية الضرب التالية

 3 ×  = □

وعليه فإن : □ =  . والشكل التالي يوضح ذلك

وضع 5 أثقال على المشجب رقم  من الذراع الأيمن، ووضع أثقال على الذراع الأيسر فيحصل التعادل بوضع ثقلين على المشجب رقم واحد بالإضافة إلى ثقل على المشجب الذي

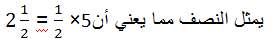
والشكل التالي يوضح الفكرة:

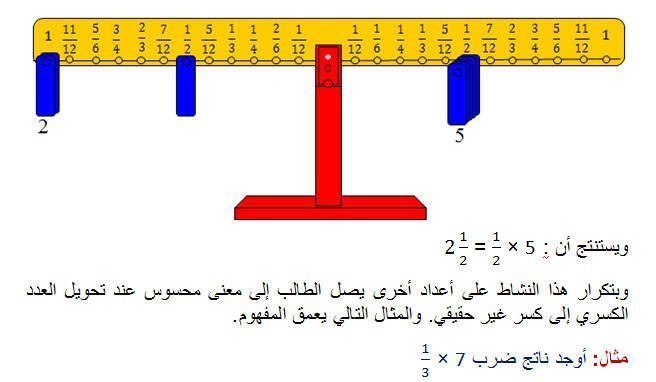
وعند وضع ثلاثة أثقال على ذلك المشجب تكون النتيجة ميل الذراع الأيسر إلى الأسفل مما يعني أنها أكبر من اللازم، عندها يكتفى بوضع ثقلين على ذلك المشجب والبحث عن مشجب آخر لنضع عليه ثقلاً واحداً يعيد التوزان، وبالبحث نجد أن ذلك المشجب هو المشجب رقم  مما يعني أن سبعة أثلاث تساوي اثنين وثلث

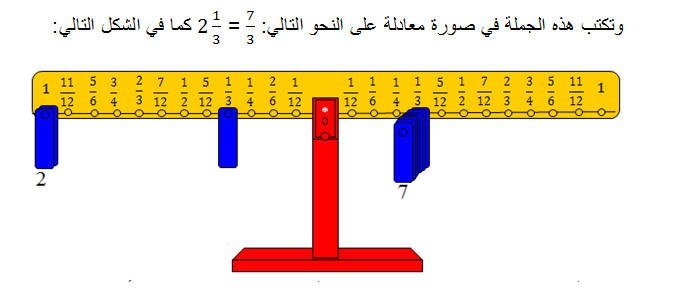
وبتكرار النشاط يستنتج الطالب طريقة كتابة العدد الكسري في صورة كسر غير حقيقي

ثم يتدرج الطالب ليصل إلى دراسة ضرب عدد صحيح في كسر (غير كسر الوحدة) كأن يضرب   6 ×  = □

ولا حتى ثقلين أو ثلاثة أثقال، وعند وضع ثقل رابع على المشجب الذي يمثل الواحد يحصل التوازن مما يعني أن حاصل الضرب هو 4. والشكل التالي يوضح الفكرة

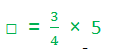
فيتم تمثيلها بطريقة مشابهة بوضع خمسة أثقال على المشجب الذي يمثل  وإعادة التوزان بوضع أثقال على المشجب رقم واحد من الذراع الأيسر، وحيث إن ثلاثة أثقال على ذلك المشجب لا تكفي لإعادة التوازن، وأن أربعة أثقال على ذلك المشجب أكثر من اللازم وجب وضع ثلاثة أثقال على المشجب رقم واحد وثقل على المشجب الذي يمثل ثلاثة أرباع مما يعني أن : □ =  

والشكل التالي يوضح ذلك

أما عمليات ضرب عدد صحيح في عدد كسري كضرب

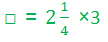
فيتم على النحو التالي:

 تكرار هذه الخطوة بعدد مرات العدد الصحيح، مما يعني في نهاية الأمر وضع 6 أثقال على المشجب رقم 1 ، وثلاثة أثقال على المشجب رقم  فينحرف الذراع الأيمن

والشكل التالي يوضح ذلك

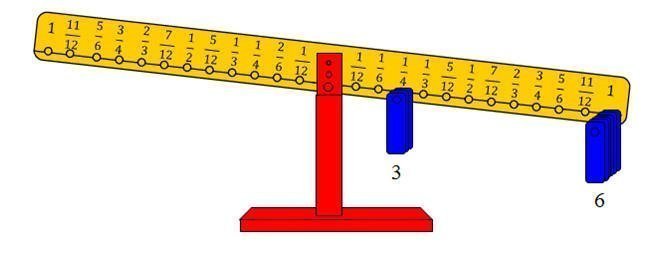
 يساوي 6 أثقال على المشجب رقم1 بالإضافة إلى ثقل واحد نضعه على المشجب الذي يعيد التوازن وهو المشجب رقم  

 والشكل التالي يوضح الفكرة

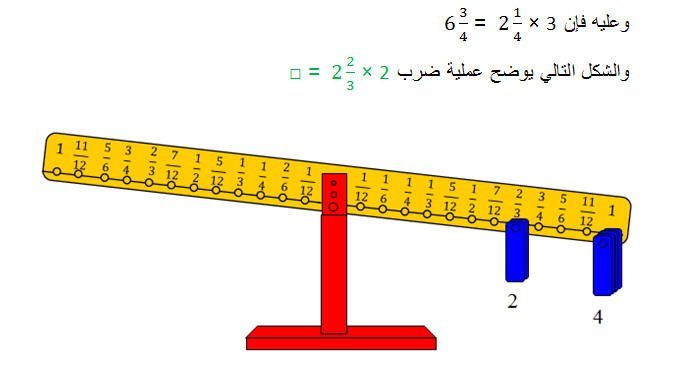
حيث تم تمثل العدد الكسري بوضع ثقل على المشجب الذي يمثل الثلثين، وثقلين اثنين على المشجب رقم واحد. وتكرار ذلك مرتين (عدد مرات العدد الصحيح)

مما يعني أن أربعة أثقال على المشجب رقم 2 وثقلين على المشجب الذي يمثل الثلثين. وعند ومحاولة إعادة التوازن تم وضع خمسة أثقال على المشجب رقم واحد من الذراع الأيسر،

إلا أنها لا تكفي لإعادة التوازن، وعند وضع ثقل سادس يميل الذراع الأيسر إلى الأسفل، مما يعني أن ذلك العدد أكبر من اللازم، وعليه تم البحث عن مشجب آخر يعيد التوازن بالإضافة إلى الخمسة أثقال الموجودة على المشجب رقم واحد وهو المشجب رقم  

ويكمن تطبيق قاعدة توزيع الضرب على الجمع التي تعلمها الطالب على الأعداد الصحيحة عند ضربه عدد صحيح × عدد كسري، وحيث إن القاعدة تنص على أن:

أ × ب + أ × ج = أ ( ب + ج)

فإنه يمكن تطبيقها على المثال السابق.

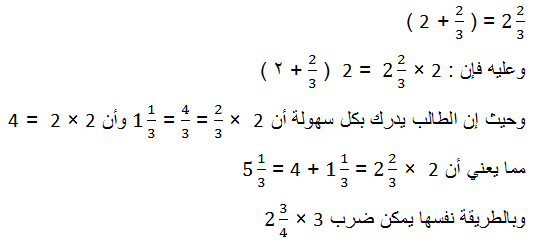
وهذه القاعدة تنص جبرياً على أن:

( أ + ب ) ( ج + د ) = ( أ × ج ) + ( أ × د ) + ( ب × ج ) + ( ب × د)

                          = أ ج + أ د + ب ج + ب د

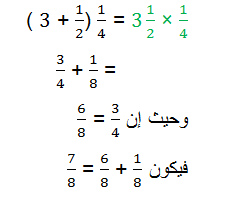
والمثال الأخير لا يمكن تمثيله على الميزان، وكذلك المسائل التي تتطلب ضرب كسر × كسر نظراً لكون الأثقال كلها ذات وزن ثابت، وحاصل الضرب كما ذكرنا هو (عدد الأثقال × قيمة المشجب) .

وحيث لا يمكن الحصول على عدد أثقال يساوي نصف أو ربع فإنه لا يمكن تمثيل ذلك على الميزان وقد تعتبر هذه نقطة الضعف الوحيدة