القسمة:

المشجب رقم 12 الذي على الذراع الأيمن يمكن استخدامه في حالة كون العدد المضروب فيه هو 12 أو كون العدد الذي نريد نجمعه مع عدد آخر هو 12، والشيء نفسه ينطبق على المشجب رقم 11

من الذراع الأيسر في حالة كون أحدهما هو المقسوم عليه في عمليات القسمة، فعلى سبيل المثال فإن عملية قسمة: 36÷12=□ يمكن تمثيلها باتباع الخطوات التالية:

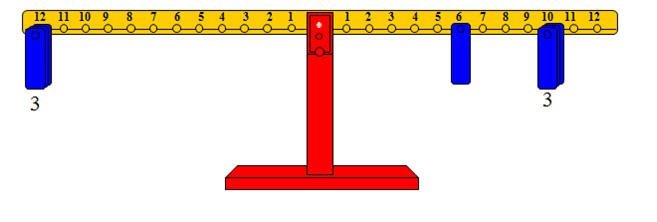
·       تمثيل العدد الأول المقسوم  على الذراع الأيمن بوضع ثقل واحد على المشجب رقم 6 وثلاثة أثقال على المشجب رقم 10.

·       وضع أثقال على المشجب رقم 12 من الذراع الأيسر لتمثيل خارج القسمة حيث12 هو المقسوم عليه وعدد الأثقال يمثل خارج القسمة.

وعليه فإن □=3

أما قسمة 35÷11=□

فيتم تمثيلها على الميزان على النحو التالي:

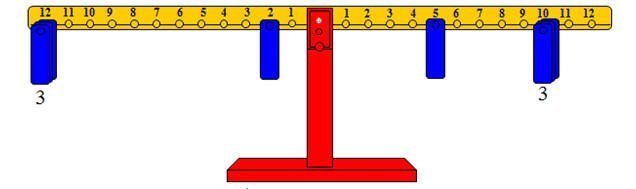
·       تمثيل المقسوم بوضع ثقل على المشجب رقم5 وثلاثة أثقال على المشجب رقم 10.

·       وضع أثقال على المشجب رقم 11 من الذراع الأيسر حيث 11 تمثل المقسوم.

·       عدد الأثقال هو خارج القسمة.

وحيث تم وضع ثلاث أثقال على المشجب رقم11 ولم يحدث توازن، ونظراً لأن ثقلاً  رابعاً يكون أكبر من المقسوم، فيجب إبقاء ثلاثة أثقال على المشجب رقم11 وثقل على المشجب الذي يعيد التوازن،

وهو المشجب رقم2، وعليه فإن :

والشكل التالي يوضح الفكرة

وبهذه الطريق يتم تمثيل عمليات القسمة التي من نوع :

 أ ÷ ب = □

أما عمليات القسمة التي من النوع:35

 ÷  □ = 7 فيتم تمثيلها باتباع الخطوات التالية :

·       تمثيل المقسوم بوضع ثقل واحد على المشجب رقم 5 وثلاثة أثقال على المشجب رقم  10من الذراع الأيمن

 لأن 35 = 5 +3 ×10 = 5 +30

·       نضع أثقالً على المشجب رقم 7من الذراع الأيسر.

·       عدد الأثقال خارج القسمة وفي هذه الحالة يكون خارج القسمة أي أن : □ =5

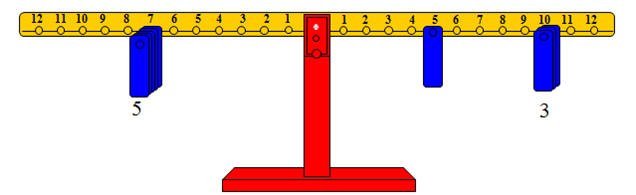
أما إذا كان المقسوم 37 والمقسوم عليه 7فإن خارج القسمة هو 5 والباقي 2