قسمة كسر على كسر:
![]() =
□
=
□
هذه المعادلة تمثل إجابة على سؤال مثل: كم ربعاً موجوداً في الثلاثة أرباع؟ أو الثلاثة ارباع فيها كم مربع؟
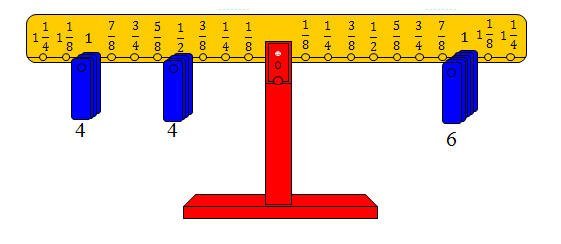
· تمثيل المقسوم بوضع ثقل على المشجب الذي يمثل الثلاثة أرباع على الذراع الأيمن.
· وضع أثقال على المشجب الذي يمثل الربع من الذراع الأيسر.
· عدد الأثقال التي تعيد الميزان إلى حالة التوازن هو خارج القسمة.
وفي هذه الحالة فإن : □ = 3، والشكل التالي يوضح الفكرة
وبالطريقة نفسها يمكن تمثيل عملية قسمة:

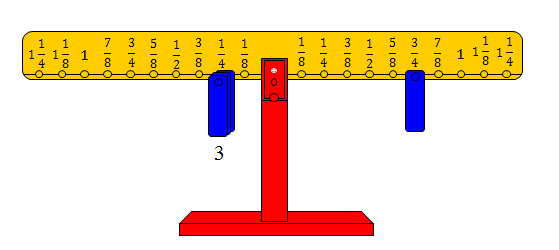
· حيث يتم وضع ثقل على المشجب الذي يمثل المقسوم على الذراع الأيمن.
· وضع أثقال على المشجب الذي يمثل المقسوم عليه على الذراع الأيسر.
· عدد الأثقال هو خارج القسمة.
وعليه فإن: □ = 4
وبتكرار العملية على أمثلة أخرى مثل :
![]() ÷
÷
![]() وغيرها
يمكن أن يتوصل الطالب إلى أن قسمة كسر على كسر يمكن أن تكتب في صورة معادلة رياضية
مثل:
وغيرها
يمكن أن يتوصل الطالب إلى أن قسمة كسر على كسر يمكن أن تكتب في صورة معادلة رياضية
مثل:
![]() +
+ ![]() =
=
كما يمكن إجراء عملية القسمة التالية:
![]() ÷
÷
![]() =
□
=
□
وذلك بتمثيل المقسوم على الذراع الأيمن بوضع ثقل على المشجب الذي يمثل الواحد صحيح ثقل آخر على المشجب الذي يمثل النصف، ثم وضع أثقال على المشجب الذي يمثل الربع من الذراع الأيسر.
عدد الأثقال على هذا المشجب الذي يمثل المقسوم عليه هو خارج القسمة.
والشكل التالي يوضح الفكرة


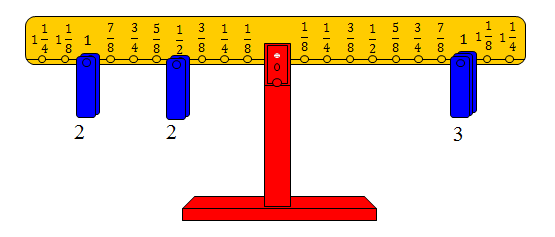
· وضع ثلاثة أثقال على المشجب رقم واحد من الذراع الأيمن.
· تحديد المشجبين اللذين يمثلان المقسوم عليه وهو الواحد والنصف.
· وضع أثقال على كل مشجب على التوالي وعدد الأثقال على أحد المشجبين هو خارج القسمة.
وحيث إنه في هذه الحالة عاد التوازن بوضع ثقلين على كل من المشجبين اللذين يمثلان المقسوم عليه وهما المشجب رقم واحد والمشجب الذي يمثل النصف.
وعليه فإن : □ = 2 . والشكل التالي يوضح الفكرة
وبالطريقة نفسها يمكن قسمة
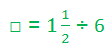
حيث يتم وضع ستة أثقال على المشجب الذي يمثل الواحد صحيح من الذراع الأيمن. والبحث عن المشجبين اللذين يمثلان المقسوم عليه ووضع أثقال بالتناوب على كل مهما حتى يحث التوازن.
وعدد الأثقال على أي منهما هو خارج القسمة.
وفي هذه الحالة فإن : □ = 4 . الشكل التالي يوضح الفكرة