قسمة عدد على كسر

قسمة الكسور الاعتيادية:

قسمة الواحد صحيح على كسر الوحدة.

مثال :  1 ÷  = □

العملية يمكن أن تترجم إلى السؤال التالي:كم نصفاً موجود في الواحد صحيح؟

ولتمثيل ذلك على الميزان يتم وضع ثقل واحد على المشجب الذي يمثل الواحد صحيح من الذراع الأيمن. وعلى الذراع الأيسر نضع أثقالاً على المشجب الذي يمثل النصف.

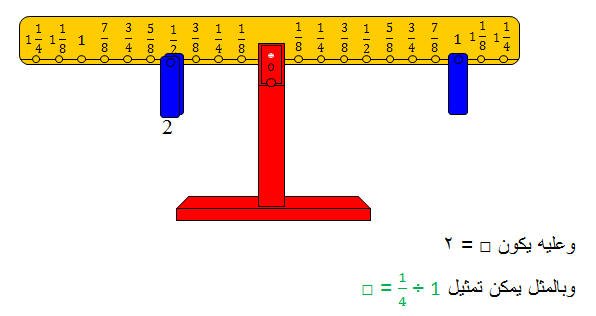
وتكون الإجابة □ = 4

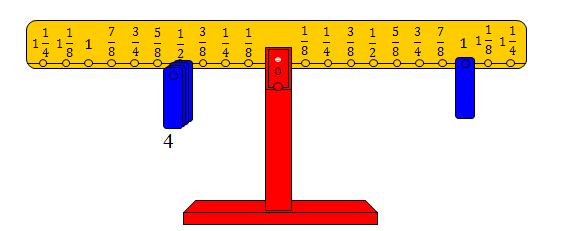
حيث تم تمثيل الواحد بوضع ثقل على المشجب الذي يمثل الواحد صحيح من الذراع الأيمن، وعلى الذراع الأيسر وضعنا ثقلاً على المشجب الذي يمثل الربع.

وكان عدد الأثقال الذي أعادت التوازن على ذلك المشجب هي أربعة أثقال مما يعني أن : □ = 4.

وبصورة عامة فإن خارج قسمة الواحد صحيح على كسر الوحدة يساوي مقام الكسر.

ويمكن كتابة ذلك في صورة معادلة رياضية:

قسمة عدد صحيح على كسر الوحدة:

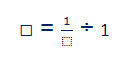
عملية قسمة 2 ÷  = □      يمكن أن تكون إجابة على السؤال التالي: الاثنين تحتوي على كم ربع؟ أو  كم ربعاً موجود في العدد اثنين؟

لتمثيل ذلك ضع ثقلين على المشجب الذي يمثل الواحد من الذراع الأيمن. وعلى الأيسر ضع أثقالاً على مشجب الربع. عدد الأثقال هو الجواب

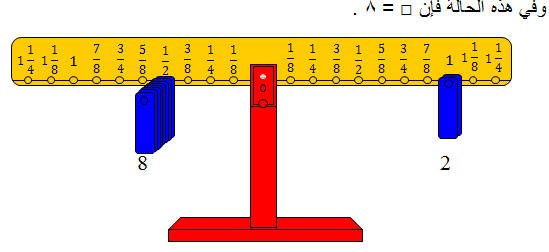
أما عملية عملية قسمة : 3 ÷  = □

وعدد الأثقال يساوي خارج القسمة. وفي هذه الحالة فإن : □ = 6 كما في الشكل التالي

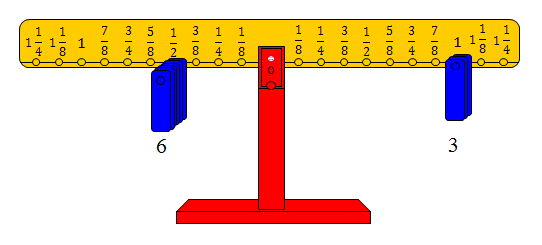
وبتكرار النشاط السابق على التمارين التالية:

4 ÷  = □ ، 5 ÷  = □   وغيرها حيث

يصل الطالب إلى تعميم ينص على أن حاصل قسمة عدد صحيح على كسر الوحدة يكون خارج القسمة يساوي حاصل ضرب العدد الصحيح × مقام كسر الوحدة.

أي أن : أ ÷  = أ ب

وهكذا يرى الطالب معنى وسبب مقنع أن عملية القسمة تحول فيها إشارة القسمة إلى ضرب.