قسمة الأعداد العشرية:

حيث يتم تمثيل المقسوم على الذراع الأيمن من الميزان وتحديد مشجب المقسوم عليه على الطرف الأيسر من الميزان ووضع أثقال على هذا المشجب الذي يمثل المقسوم عليه،

ويكون عدد الأثقال هو خارج القسمة. والشكل التالي يوضح عملية القسمة السابقة

وعليه يكون خارج القسمة هو 3 أثقال أي 3   وبالتالي فإن : 0.6 ÷ 0.2 = 3

وبالطريقة نفسها يمكن تمثيل عملية القسمة التالية: 1.6 ÷ 0.8 = □

حيث يتم تمثيل المقسوم على الذراع الأيمن بوضع ثقل على المشجب رقم 0.6 وآخر على المشجب رقم واحد من الذراع الأيمن.

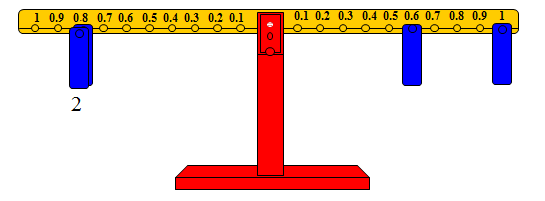
وعليه فإن خارج القسمة يساوي 2 .

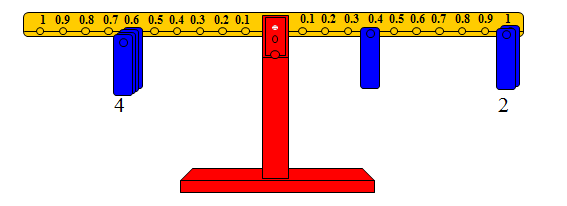
أما عملية قسمة 2.4 على 0.6 فيمكن تمثيلها على النحو التالي:

·       تمثيل المقسوم (2.4) بوضع ثقل على المشجب رقم 0.4 وثقلين اثنين على المشجب رقم واحد من الذراع الأيمن 2.4 = 0.4 + 2

·       تحديد مشجب المقسوم عليه (0.6).

·       وضع أثقال على هذا المشجب حتى يحصل التوازن.

·       عدد الأثقال تمثل خارج القسمة.

وعملية قسمة 3.6 ÷ 1.2= □ يمكن تمثيلها على الميزان عن طريق تمثيل العدد الأول (المقسوم) على الذراع الأيمن من الميزان بوضع ثقل واحد على المشجب رقم 0.6 وثلاثة أثقال

على المشجب رقم واحد من الذراع نفسه. وتمثيل العدد الثاني على الذراع الأيسر من الميزان بوضع ثقل واحد على المشجب رقم 0.2 وثقل واحد على المشجب رقم واحد.

وتكرار ذلك في كل مرة نضع ثقلاً واحداً على كلا المشجبين حتى يحدث التوازن.

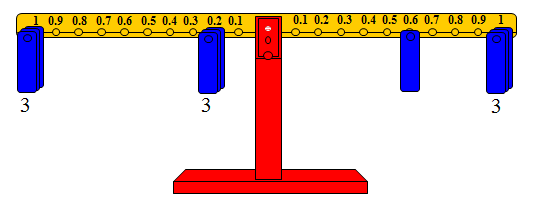
لعلك لاحظت إمكانيات الميزان الحسابي في إجراء العديد من عمليات الجمع، والطرح والضرب، والقسمة على الأعداد العشرية، ولكن هل لاحظت جوانب القصور في هذه الأداة؟

هل بالإمكان تمثيل العمليات التالية:

3.25 + 3.34

3.42 – 2.23

2.25 × 1.2

2.12 × 2.15

4.25 ÷ 1.35

بالطبع لا يمكن ذلك لأنه من غير الممكن تمثيل 0.25 على الميزان دون تعديل، فقدرة الميزان تكمن في تمثيل منزلة عشرية واحدة (جزء من عشرة فقط)

وعليه لا يمكن إجراء عمليات تحتوي على جزء من مئة دون إجراء تغيرات على الميزان.

إن الميزان لم يصمم ليقوم بإيجاد الحل مثل الآلة الحاسبة، وإنما صمم ليعطي تجسيداً محسوساً لخوارزمية العملية الحسابية، ويكتفي بتعليمك الأساسيات، ثم تنطلق من هناك،

 وبالرغم من هذا القصور هناك العديد من النواحي الإيجابية.

وهناك وسائل أخرى تغطي جوانب القصور في الميزان مثل مكعبات دينز التي يمكن بها جمع 1.25 + 3.42 أو طرح 5.24 – 2.75 مثلاً.

حيث يمثل المربع الكبير 10 سم × 10 سم في هذه الحالة الوحدة، وعليه فإن المستطيل الذي أبعاده 1 سم × 1 سم × 10 سم يمثل العشر، أما المكعب الصغير فيمثل جزء من مئة.

وحتى إذا أردنا إجراء عمليات جمع أو طرح تحتوي على جزء من ألف فإنه في هذه الحالة يعتبر المكعب الكبير الذي أبعاده 10 سم × 10 سم × 10 سم هو الواحد صحيح،

وعليه فإن المربع الكبير يمثل جزء من عشرة، والمستطيل يمثل جزء من مئة، أما المكعب الصغير فإنه يمثل جزء من ألف، وبذلك يمكن إجراء عمليات الجمع والطرح على الأعداد التي تحتوي على جزء من الألف.

وبالرغم من قدرة قطع دينز على إجراء عمليات الجمع والطرح على أعداد تحتوي على جزء من مئة أو جزء من ألف، تظل قدرتها محدودة في إجراء عمليات الضرب والقسمة،

وبالرغم من محدودية قدرتها فهي أفضل من الميزان، حيث يمكن إجراء علمية ضرب تحتوي على جزء من عشرة في كلا العددين بينما في الميزان لا يمكن ذلك.

يمثل الوحدة (كمساحة مربع) . وعليه فإن المربع الصغير في هذه الحالة يمثل جزء من مئة . فإذا أردنا ضرب1.2 × 1.3 فإننا

نقوم بتمثيل العدد الأول والعدد الثاني في هيئة مستطيل على النحو التالي:

حيث تتضح الخوارزمية للطالب ويكون الناتج ماثلاً أمامه على النحو التالي:

0.2 × 0.3 = 0.6 وهي المربعات الستة الصغيرة في الركن الأيمن للمستطيل.

0.2 × 1 = 0.2 وهما المستطيلان الموجودان على يمين المربع الكبير.

1 × 0.3 = 0.3 وهي المستطيلات الثلاثة الموجودة أسفل المربع الكبير.

1 × 1 = 1 وهو المربع الكبير داخل المستطيل . وعند جمع هذه الأعداد نحصل على :

0.06 + 0.2 + 0.3 + 1 = 1.56

إن التقسيم الجديد لذراعي الميزان الذي يجعل الثمانية المشاجب الأولى بدءاً من المركز تمثيل للواحد الصحيح، يتيح الفرصة أمام الطلاب لدراسة العلاقة بين الكسر الاعتيادي والكسر العشري،

حيث يتم ترقيم مشاجب الذراعين وفقاً للجدول التالي

وهذا التقسيم يوضح كتابة الكسور الاعتيادية في صورة عشرية، فالثمن مثلاً يساوي 0.125 في حين أن الربع يساوي 0.25 أما الثلاثة أثمان فإنها تساوي 0.375،

وكما أمكننا الاستفادة من هذا التقسيم في دراسة العمليات الحسابية على الأعداد العشرية يمكننا الاستفادة في دراسة الكسور الاعتيادية وإجراء العمليات عليها.

حتى يتمكن الطالب من دراسة الكسور المكافئة حيث يضع الطالب ثقلين اثنين على الجانب الأيمن على المشجب الذي يمثل الثمن ويعادلها بثقل واحد على الذراع الأيسر

 فيجد أن الثمنين تساوي الربع. أما الأربعة أثقال على المشجب الذي يمثل الثمن من الذراع الأيمن فإنها تعادل ثقل واحد على المشجب الذي يمثل النصف.

هذا من ناحية، ومن ناحية أخرى فإن وضع ثقل واحد على المشجب الذي يمثل  على الذراع الأيمن يعادل ثقلين على الجانب الأيسر أحدهما على المشجب الذي يمثل الثمن والآخر على المشجب

الذي يمثل الواحد صحيح