ضرب الأعداد العشرية:

يمكن إجراء عملية ضرب عدد صحيح في عدد عشري (مكون من عدد صحيح وجزء من عشرة) ولا يمكن إجراء عمليات ضرب (عدد عشري × عدد عشري) ،

وهذه النقطة تمثل إحدى جوانب القصور في الميزان الحسابي كما سيأتي شرح ذلك.

عملية ضرب 3 × 0.5 يمكن تمثيلها بوضع ثلاثة أثقال على المشجب رقم 0.5 على الذراع الأيمن ومحاولة إعادة التوازن بوضع أثقال على الذراع الأيسر من الميزان.

وحيث إن ثقلاً واحداً لا يكفي لإعادة التوازن عند وضعه على المشجب رقم واحد من الميزان، وأن ثقلين على ذلك المشجب أكبر من حاصل الضرب، مما يعني إبقاء ثقل واحد على المشجب رقم واحد،

والبحث عن المشجب الذي نضع عليه الثقل الثاني لإعادة التوازن.

      والشكل التالي يوضح الحل حيث 3 × 0.5 = 1.5

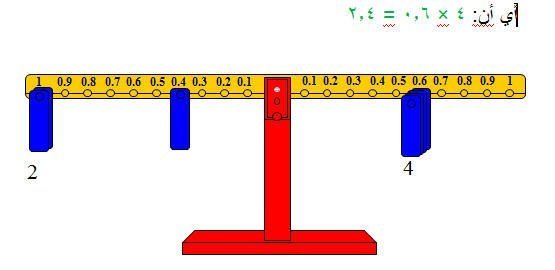
عملية ضرب 4 × 0.6 يمكن تمثيلها بوضع أربعة أثقال على المشجب رقم 0.6 على الذراع الأيمن من الميزان، ومحاولة إعادة التوازن على الذراع الأيسر،

 وحيث إن ثقلاً واحداً على المشجب رقم واحد لا يكفي لإعادة التوازن، كما أن وضع ثقلين اثنين على ذلك المشجب لا يكفي لإعادة التوازن، وأن ثلاثة أثقال

على المشجب رقم واحد أكبر من حاصل الضرب، مما يعني الإبقاء على ثقلين في المشجب رقم واحد، وبالبحث عن المشجب الذي عنده نضع ثقلاً ويعيد التوازن،

 نجد أنه المشجب رقم 0.4

وعملية ضرب 4×1.2

تتم على النحو التالي:

·       تحديد المشجبين اللذين يمثلان العدد الثاني وهما المشجب رقم 0.2 والمشجب 1 على الذراع الأيمن.

·       وضع أربعة أثقال على كل مشجب من المشجبين .

·       البحث عن المشجب الذي يعيد التوازن على الذراع الأيسر.

وحيث إن حاصل ضرب الجزء الصحيح من العدد العشري في العدد الصحيح (4) = 4 فإن معنى ذلك وضع أربع أثقال على المشجب رقم (1) على الذراع الأيسر،

وعند وضع ثقل خامس يميل الذراع الأيسر، دلالة أن 5 أثقال أكبر من حاصل الضرب، مما يعني الإبقاء على الأربعة أثقال على المشجب رقم واحد من الذراع الأيسر

 والبحث عن المشجب الذي عند وضع الثقل الخامس عليه يحصل التوازن، وبالبحث نجد أن المشجب رقم 0.8 ، وعليه فإن الإجابة هي 4.8.

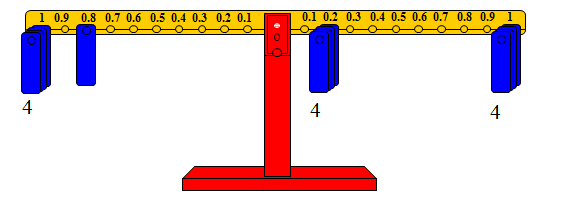
أما عملية ضرب 3 × 2.5 فيمكن حلها باستخدام الميزان على النحو التالي:

·       تمثيل العدد 2.5 بوضع ثقل على المشجب رقم 0.5 وآخرين (ثقلين اثنين) على المشجب رقم واحد من الذراع الأيمن للميزان وتكرار هذه الخطوة حتى يكون إجمالي التكرارات هو العدد الصحيح (3).

وبما أنه كان على المشجب رقم واحد ثقلين وأضفنا إليهما أربعة أثقال فإن الناتج يكون ستة أثقال على هذا المشجب. أما المشجب رقم 0.5 فكان عليه ثقل واحد أضفنا إليه ثقلين اثنين فأصبح على هذا المشجب ثلاث أثقال.

وعند محاولة إيجاد التوازن بوضع 5 أثقال على المشجب رقم واحد من الذراع الأيسر نجد أنها بالطبع لا تكفي، وعند وضع ثقل سادس كذلك لا يتم التوازن، وعند وضع ثقل سابع لا يتم التوازن، أما إذا وضعنا

ثقلاً ثامناً فإن الذراع الأيسر يميل مما يعني أن ثمانية أثقال أكبر من حاصل الضرب.

مما يعني أن الإجابة هي 7.5 والشكل التالي يوضح الفكرة

وبالطريقة نفسها يمكن إجراء عمليات ضرب عدد صحيح ضرب عدد عشري مكون من عدد صحيح وجزء من عشرة