الأعداد الزوجية والأعداد الفردية:

كل الأعداد التي تقبل القسمة على 2 بدون باقي هي أعداد زوجية، أما الأعداد التي عند قسمتها على 2 ولها باق فإنها أعداد فردية.

وباستخدام الميزان يمكننا الكشف عن كون العدد زوجي أم فردي، وذلك بتمثيل العدد الذي نريد اختباره على الذراع الأيمن من الميزان، ونضع أثقالاً على المشجب رقم 2 من الذراع الأيسر، فإن كان هناك توازن دون إضافة ثقل على مشجب آخر كان العدد زوجياً.

فعلى سبيل المثال العدد 14 عدد زوجي لأن حاصل قسمته على 2 يكون سبعة والباقي صفراً والشكل التالي يوضح التمثيل

 

حيث تم تمثيل العدد 14 بوضع ثقل على المشجب رقم 4 وآخر على المشجب رقم 10 من الذراع الأيمن. وعند وضع أثقال على المشجب رقم 2 من الذراع الأيسر كان عدد الأثقال سبعة مما يعني أن خارج القسمة يساوي سبعة وليس هناك حاجة لإضافة أي ثقل على أي مشجب آخر لإعادة التوازن، مما يعني أن العدد 14 هو عدد زوجي.

أما العدد 15 مثلاً فهو عدد فردي، لأنه لا يقبل القسمة على 2 بدون باقي، والشكل التالي يمثل الحالة:

حيث تم تمثيل العدد 15 بوضع ثقل على المشجب رقم 5 وآخر على المشجب رقم 10 على الذراع الأيمن، وبوضع أثقال على المشجب رقم 2 اتضح أن 7 أوزان لا تكفي لإعادة التوازن وأن 8 أثقال على المشجب رقم 2 أكبر من 15 مما يعني أن خارج القسمة يساوي 7 والباقي واحد. أي أن العدد 15 هو عدد فردي

ادرس الجدول التالي واكتب ملاحظاتك.

العدد	يقبل القسمة على 2	خارج القسمة	الباقي	فردي/زجي
0	نعم	0	0	زوجي
1	لا	0	1	فردي
2	نعم	1	0	زوجي
3	لا	1	1	فردي
4	نعم	2	0	زوجي
5	لا	2	1	فردي
6	نعم	3	0	زوجي
7	لا	3	1	فردي
8	نعم	4	0	زوجي
9	لا	4	1	فردي
10	نعم	5	0	زوجي
11	لا	5	1	فردي
12	نعم	6	0	زوجي
13	لا	6	1	فردي

          §          الأعداد التي لا تقبل القسمة على 2 هي أعداد فردية.

          §          الأعداد الزوجية هي مضاعفات للعدد 2 أي 2 × ن.

          §          هل لاحظت أن الأعداد الفردية عند قسمتها على 2 كان الباقي دائماً واحد؟

          §          هل يمكن كتابة الصيغة العامة للأعداد الفردية على صورة 2ن؟

          §          ماذا تقترح؟

          §          هل الصيغة العامة للأعداد الفردية هي ( 2 ن + 1 )؟

مجموع عددين زوجين:

بعد أن تعرفت على كيفية اختبار العدد الزوجي، يمكنك تحديد نوع العدد هو هو زوجي أم فردي؟ ولكن ماذا عن مجموع عددين زوجيين ، أو مجموع عددين فرديين، أو مجموع عددين أحدهما فردي والآخر زوجي؟

هل مجموع عددين زوجيين هو عدد زوجي أم فردي؟

لمعرفة ذلك ما عليك سوى اختبار عددين زوجيين وتمثيل كل منهما على الذراع الأيمن من الميزان، وتمثيل مجموعهما على المشجب رقم 2 ، فإن كان مجموعهما يساوي عدداً معيناً من الأثقال على المشجب رقم 2 فقط، فإن المجموع عدد زوجي ، أما إذا كان مجموع العددين يساوي عدداً معيناً من الأثقال على المشجب رقم 2 بالإضافة إلى ثقل واحد على المشجب رقم واحد فإن المجموع يكون عدداً فردياً.

مثال: هل مجموع العددين 4 ، 2 عدد زوجي أم فردي؟

لمعرفة ذلك قم بتمثيل العدد 4 على الذراع الأيمن وكذلك العدد 2 ، ثم ضع أثقالاً على المشجب رقم 2 من الذراع الأيسر حتى يعود الميزان إلى حالة التوازن.

والشكل التالي يوضح أن : 4 + 2 = عدد زوجي

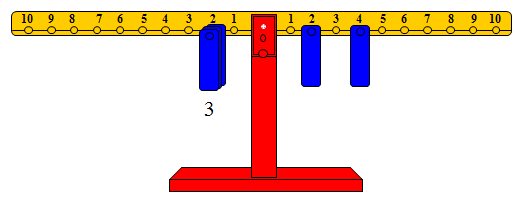
والشكل التالي يوضح أن : 6 + 8 = عدد زوجي:

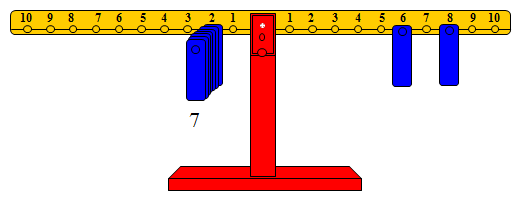
حيث تم تمثيل العدد الأول بوضع ثقل على المشجب رقم 6 على الذراع الأيمن وثقل آخر على العدد 8 لتمثيل العدد الثاني على الذراع نفسه. ولمعرفة ما إذا كان مجموع العددين عدد فردي أو زوجي نضع أثقالاً على المشجب رقم 2 من الذراع الأيسر.

وحيث أن 7 أوزان أعادت التوازن دون الحاجة إلى المشجب رقم واحد، إن هذا معناه أن المجموع عدد زوجي.

وبالطريقة نفسها يمكن اختبار المجموع وكونه عدد زوجي أم فردي في حالة أحد العددين أو كلاهما مكون من رقمين فالعددين 12 ، 6 مجموعهما عدد زوجي حيث تم تمثيل العدد 12 بوضع ثقل على المشجب رقم 2 وآخر على المشجب رقم عشرة من الذراع الأيمن، أما العدد الثاني فتم تمثيله بوضع ثقل على المشجب رقم 6 من الذراع نفسه، ولإعادة التوازن نحتاج إلى 9 أثقال على المشجب رقم 2 من الذراع الأيسر دون الحاجة إلى المشجب رقم واحد.

والشكل التالي يوضح الفكرة

مما يعني أن:

عدد زوجي + عدد زوجي = عدد زوجي

 

مجموع عددين فردين:

بالطريقة نفسها قم باختيار عددين فرديين على الذراع الأيمن وحاول إعادة التوازن باستخدام أثقال على المشجب رقم 2 فقط على الذراع الأيسر وتعرف على مجموعهما.

مثال: هل مجموع 3 + 5 عدد فردي أم زوجي؟

الشكل التالي يوضح المجموع

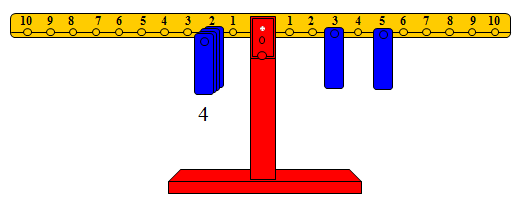
وحيث أن مجموعهما يساوي 4 × 2 فإن المجموع هو عدد زوجي، مما يعني أن :

فردي + فردي = زوجي

 

والمثال التالي يؤكد صحة ذلك:

اجمع 7 + 9 وحدد نوع مجموعهما هل هو عدد فردي أم عدد زوجي؟

الحل:

تمثيل العدد الأول بوضع ثقل على المشجب رقم 7 على الذراع الأيمن وكذلك العدد الثاني بوضع ثقل على المشجب رقم 9 على الذراع نفسه، ثم وضع أثقال على المشجب رقم 2 من

الذراع الأيسر فنلاحظ أن التوازن قد عاد إلى الميزان عند وضع 8 أثقال على هذا المشجب مما يعني أن العددين موجبان.

والشكل التالي يوضح الفكرة

 

والآن دعنا ندرس حالة كون أحد العددين المجموعين زوجي والآخر فردي، كأن يكون أحدهما 6 والآخر 3 ونحكم على المجموع.

قم بتمثيل العدد الأول بوضع ثقل على المشجب رقم 6 من الذراع الأيمن وثقل على المشجب رقم 3 من الذراع الأيمن، حاول إعادة التوازن على المشجب رقم 2، فإن لم يحدث التوازن أضف ثقلاً واحداً على المشجب رقم واحد من الذراع الأيسر.

وفي هذه الحالة عند محاولة إيجاد التوازن وضعنا 4 أثقال على المشجب رقم 2 دون أن يحدث التوازن وعند إضافة ثقل خامس اتضح أن خمسة أثقال أكبر من مجموع العددين مما يعني أن التوازن يتحقق بأربعة أثقال على المشجب رقم 2 وثقل واحد على المشجب رقم واحد بالذراع الأيسر.

وعليه فإن مجموع العددين 6 ، 3 عدد فردي، والشكل التالي يوضح الفكرة.

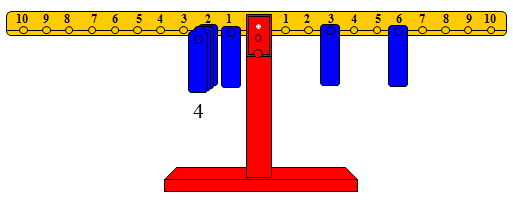
وللتأكد من القاعدة حاول إيجاد مجموع العددين 5 ، 8 باتباع الطريقة السابقة حيث تم تمثيل كل من العددين على الذراع الأيمن ومحاولة إعادة التوازن على المشجب رقم 2 من الذراع الأيسر فقط فإن لم نتمكن نستخدم ثقلاً واحداً على المشجب رقم واحد كما في الشكل التالي

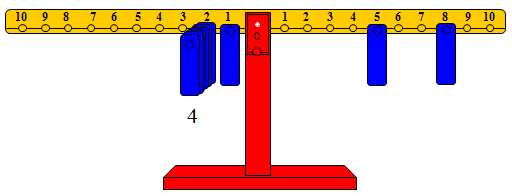
حيث إن ستة أثقال على المشجب رقم 2 من الذراع الأيسر لا تكفي لإعادة التوازن وأن سبعة أثقال تكون أكبر من الذراع الأيمن وعليه فإن ستة أثقال على المشجب رقم 2 بالإضافة إلى ثقل على المشجب رقم واحد تكفي لإعادة التوازن

مما يعني أن 5 + 8 = فردي