مضاعفات العدد:
من المكن استخدام الميزان لشرح مضاعفات العدد وذلك بإضافة أوزان إلى العدد نفسه، فالعدد 3مثلاً يتم تمثيله على ذراع الميزان الأيمن ويتم توازن الميزان بإضافة ثقل على الذراع الأيسر. أما المضاعف الثاني للعدد 3 فيمكن الحصول عليه بإضافة ثقل آ على المشجب رقم 3 من الذراع الأيمن وعليه فإن 2×3= 6.
وللحصول على المضاعف الثالث للعدد 3 نضع ثقلاً ثالثاُ على المشجب نفسه ويكون الناتج 3×3=9، وهكذا.
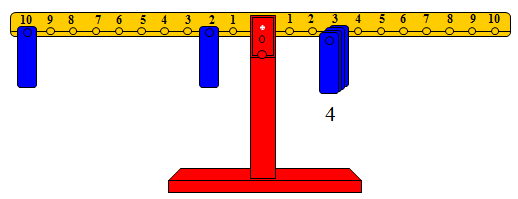
والشكل التالي يوضح المضاعف الرابع للعدد3 حيث تم وضع أربع أثقال على المشجب رقم 3 من الذراع الأيمن وإعادة التوازن بوضع ثقل واحد على المشجب رقم 2 وآخر على المشجب رقم 10 من الذراع الأيسر ليكون الناتج 4×3 =12.
المضاعف المشترك الأصغر لعددين:
ويتم تسجيل المضاعف لعددين في جدول كالتالي:
|
العدد |
المضاعف |
|||||
|
الأول |
الثاني |
الثالث |
الرابع |
الخامس |
السادس |
|
|
3 |
3 |
6 |
9 |
12 |
14 |
18 |
|
4 |
4 |
8 |
12 |
16 |
30 |
24 |
وبالطريقة نفسها يمكن معرفة مضاعفات العدد12 ومضاعفات العدد 18 وتسجيل المضاعف لكل منهما في جدول كالتالي:
|
العدد |
المضاعف |
|||||||
|
12 |
12 |
- |
24 |
36 |
48 |
- |
60 |
72 |
|
18 |
- |
18 |
- |
36 |
- |
54 |
- |
72 |
أول مضاعف مشترك للعددين 12، 18 هو العدد 36 وهو يسمى المضاعف المشترك الأصغر، ويسمى كذلك لأن العددين 12،18 مضاعفات أخرى مشتركة أكبر من 36 مثل 72. إن إيجاد المضاعف المشترك الأصغر لعددين بهذه الطريقة قد يكون مرهقاً ويستغرق وقتاً طويلاً.
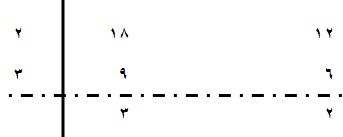
حيث تم البحث عن قاسم مشترك للعدديين 12،18 وهو العدد 2 بمعنى أن 12 تقبل القسمة على 2وكذلك 18 تقبل القسمة على 2.
الخطوة التالية هي البحث عن عدد (قاسم مشترك) بين العدد الناتجين من الخطوة السابقة وهما (6،9) وهذا القاسم المشترك الأصغر 3، وعليه فإن خارج قسمة 9÷3=3 وخارج قسمة 6÷3=2.
والآن تبقى لدينا العددين 2، 3 وليس هناك قاسم مشترك بينهما سوى الواحد وعليه فإن القاسم المشترك الأكبر للعددين 12،18 هو 2×3=6.
(نضع الخط الأفقي قبل آخر عددين لا يوجد بينهما قاسم مشترك).
أما المضاعف المشترك الأصغر للعددين 12،18 فيمكن الحصول عليه بضرب الأعداد التي تمثل القاسم المشترك الأكبر (العمود) 2×3 في الأعداد المتبقية ( التي تحت الخط). وعليه فإن المضاعف المشترك الأصغر للعددين 12،18هو:
2×3×2×3=36
وهو العدد الذي حصلنا عليه بالطريقة المطولة.
وباستخدام أشكال فن (vinn diagrams) يمكن تمثيل القاسم المشترك الأكبر في منطقة التقاطع لدائرتين إحداهما تمثل العدد الأول والأخرى تمثل العدد الثاني. فعلى سبيل المثال العددين 12، 18 يمكن تمثيلهما بدائرة لكل منهما وقاسمهما المشترك الأكبر 6 في منطقة التقاطع على النحو التالي:
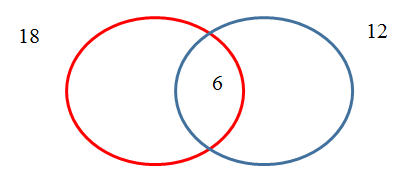
وخارج قسمة العدد الأول على القاسم المشترك الأكبر يكتب داخل الدائرة الأولى، وخارج قسمة العدد الثاني على القاسم المشترك الأكبر يكتب داخل الدائرة الثانية كما يلي
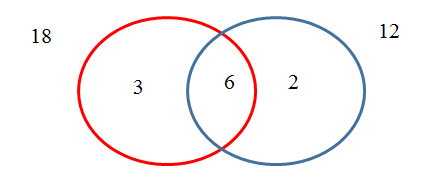
حاصل ضرب الأعداد الثلاثة التي داخل الدائرتين هو المضاعف المشترك الأصغر للعددين 12، 18.وعليه فإن المضاعف المشترك الأصغر للعددين 12 ، 18 هو: 2 × 6 × 3 = 36.
وهناك طريقة حسابية مجردة يمكن بها إيجاد المضاعف المشترك الأصغر لعددين عند معرفة قاسمهما المشترك الأكبر تتلخص في المعادلة التالية:
|
حاصل ضرب العددين = القاسم المشترك الأكبر × المضاعف المشترك الأصغر |
أو بمعنى آخر:
|
المضاعف المشترك الأصغر = حاصل ضرب العددين ÷ القاسم المشترك الأكبر |
وعليه فإن المضاعف المشترك الأصغر للعددين 12، 18 وفق المعادلة السابقة عبارة عن:
(12 × 18 ) ÷ 6 = 36
وهو الناتج الذي حصلنا عليه من الدائرتين المتقاطعتين.