4القسمة:

هي العملية العكسية للضرب، وتتلخص العملية في إيجاد أحد عاملي الضرب عندما يعرف حاصل الضرب والعامل الآخر. فعلى سبيل المثال 12 = 2 × □ تسأل عن عدد عند ضربه في 2 نحصل على العدد 12. ذلك العدد الذي نبحث عنه يمكن تمثيله بالمربع "□" أو كم بمعنى 2 في كم تساوي 12.

ولحل مسألة القسمة باستخدام الميزان يتم تمثيل (المقسوم) 12 على الذراع الأيمن للميزان، وعلى الطالب أن يكشف عدد الأوزان التي يجب وضعها على المشجب رقم 2 (المقسوم عليه) على الذراع الأيسر لإعادة التوازن.

والشكل التالي يوضح الفكرة.

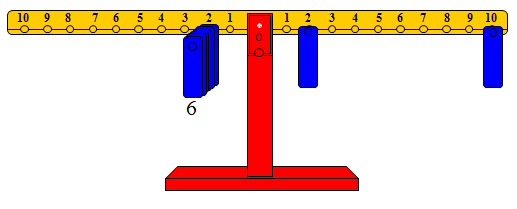
ومن الشكل يتضح أن ستة أوزان على المشجب رقم 2 من الذراع الأيسر تمثل العدد 12 على الذراع الأيمن، وأن العدد 12 تم تمثيله بثقل واحد على المشجب رقم 2 وثقل واحد على المشجب رقم 10 من الذراع الأيمن.

والشكل التالي يوضح عملية قسمة 24 ÷ 6

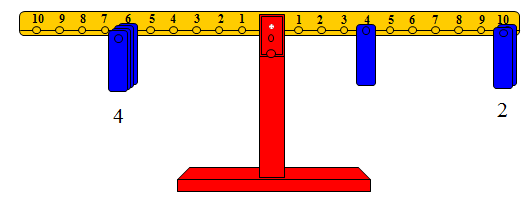
حيث تم تمثيل العدد المقسوم بثقل واحد على المشجب رقم 4 على الذراع الأيمن وثقلين على المشجب رقم 10 من الذراع نفسه 24 = 4 + 2 × 10.

خارج القسمة هو عدد الأثقال التي نضعها على المشجب رقم 6 "المقسوم عليه" على الذراع الأيسر، هذا العدد الذي يعيد التوازن باستخدام المشجب رقم 6 هو خارج القسمة.

وتصبح المعادلة 24 ÷ 6 = □ تعني الإجابة على السؤال التالي:

ما عدد الأثقال التي نضعها على المشجب رقم 6 وتعيد التوازن للذراع؟

أي بمعنى آخر كم ستة موجودة في ال 24؟

أو ما عدد المجموعات التي يمكن تكوينها من العدد 24 ويكون في كل مجموعة 6 عناصر؟

والشكل التالي يوضح عملية قسمة 18 ÷ 3

 

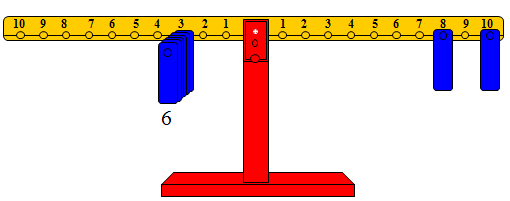
حيث تم تمثيل العدد الأول (المقسوم) على الذراع الأيمن من الميزان بوضع ثقل واحد على المشجب رقم 8 وثقل واحد على المشجب رقم 10. وتم وضع 6 أثقال على مشجب (المقسوم عليه) وهو المشجب رقم 3 . وعليه فإن الإجابة تكون 6.

أما قسمة 18 ÷ 6 = □ فتعني الإجابة على السؤال التالي:

إلى كم مجموعة يمكن تقسيم العدد 18 إذا كانت المجموعة الواحدة بها 6 عناصر؟

وبالطريقة نفسها يمكن تمثيل العدد المقسوم (18) بوضع ثقل على المشجب رقم 8 وآخر على المشجب رقم 10 على الذراع الأيمن ثم تمثيل المقسوم عليه وهو العدد (6) بوضع ثقل واحد على المشجب رقم 6 على الذراع الأيسر، فنجد أن ثقلاً واحداً لا يكفي وحتى إذا وضعنا ثقلين على المشجب نفسه فإن ذلك لا يعادل الميزان، وفي حالة وضعنا لثقل ثالث على المشجب ذاته نلاحظ أن التوازن عاد إلى الميزان. وعليه فإن الإجابة تعني ثلاثة.

والأمثلة السابقة توضح للطالب العلاقة بين القسمة والضرب

فقسمة 18÷ 3 = 6 وقسمة 18 ÷ 6 = 3 ناتجتان عن ضرب 3 × 6 = 18

وهكذا يستنتج الطالب أن عملية الضرب ينتج عنها عمليتي قسمة.

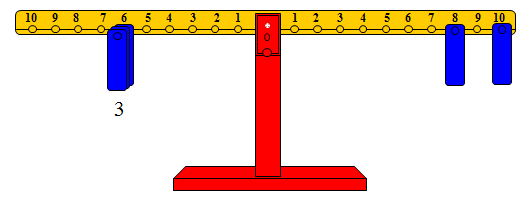
والشكل التالي يوضح خارج القسمة 18 ÷ 6 = □ حيث □ = 3.

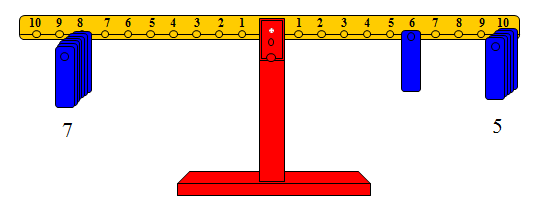
أما قسمة 56 ÷ 8 يمكن تمثيلها على النحو التالي:

·       تمثيل المقسوم (56) على الذراع الأيمن من الميزان بوضع 5 أوزان على المشجب رقم 10 ووزن واحد على المشجب رقم 6 لآن 56 = 6 + 5 × 10.

·       وضع أوزان على المشجب الذي يمثل المقسوم عليه حتى يتعادل الميزان.

·       عدد الأوزان التي أحدثت التوازن هو خارج القسمة.

والشكل التالي يوضح الفكرة

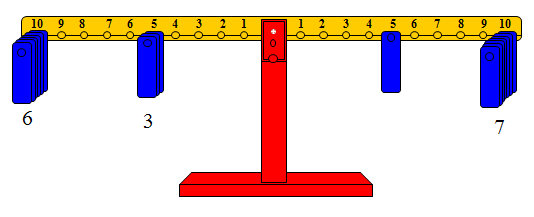
مثال (3) قسمة 75 ÷ 25.

باتباع الخطوات السابقة فإن خارج القسمة يساوي 3 (عدد مرات تكرار التمثيل).

وهكذا يرى الطالب ويدرك مفهوم القسمة والعلاقة بينها وبين الضرب حيث إن:

75 ÷ 25 = 3 أي أن 3 × 25 =

وبالطريقة نفسها يمكن تمثيل جميع عمليات القسمة المنتهية.

ولربط علمية القسمة (12 ÷ 2 ) بالطرح المتكرر يتم إزالة وزن واحد على المشجب رقم 2 (الذي يحتوي على ستة أوزان) على الذراع الأيسر مقابل تحريك الثقل الموجود على الذراع الأيمن على المشجب رقم 2 مسافتين نحو المركز مما يعني إلغاء الثقل الموجود على هذا المشجب. وإذا أردنا إزاحة ثقل آخر من الأوزان المتبقية (الخمسة) الموجودة على الذراع الأيسر، علينا أن نلجأ إلى الوزن الموجود في المشجب رقم 10 في الذراع الأيمن وتحريكه في اتجاه المحور مسافتين ليصبح على المشجب رقم 8، وفي كل مرة نطرح (نحذف) فيها ثقلاً من الجانب الأيسر يجب الإزاحة بمقدار مسافتين في اتجاه المركز على الذراع الأيمن. وبهذه الطريقة يمكن أن يفهم الطفل أن القسمة هي عملية طرح مكرر. كما يمكن تكرار هذه العملية على جدول 3 ، وجدول 4 ، لتتضح الصورة من أن القسمة هي عملية طرح تكراري، كما أن الضرب عملية جمع تكراري في الأعداد الصحيحة.

هذا ويجب عدم استخدام الميزان لإجراء عمليات الضرب والقسمة التي تتضمن أعداداً كبيرة. فالمهم إدراك المفهوم من الضرب والقسمة، وعندها يمكن استخدام أساليب أخرى لإجراء العمليات على الأعداد الكبيرة، إلا أن هذا لا يمنع من استخدام الميزان في شرح عمليات ضرب عدد مكون من رقمين في عدد مكون من رقم واحد فحاصل ضرب 3 × 12 يمكن تمثيله على الميزان وذلك بتمثيل العدد 12 بوضع ثقل واحد على المشجب رقم 10 وثقل واحد على المشجب رقم 2 وكلا الثقلين في جهة واحدة من الذراع الأيمن. وتكرار هذا التمثيل بعدد مرات العدد الأول ( 3 مرات) ومحاولة إعادة التوازن إلى الميزان بوضع أثقال على الذراع الأيسر من الميزان، والشكل التالي يمثل إحدى الصور.

 

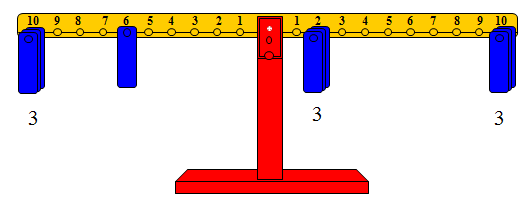
حيث تم وضع 3 أوزان على المشجب رقم 10 وثلاثة أوزان على المشجب رقم 2 وهكذا يرى الطالب أن:

3 × 12 = 3 × 2 + 3 × 10

= 6 + 30

= 36

 

وفي الوقت نفسه يرى مفهوم توزيع الضرب على الجمع في تجسيداً ملموساً.

  

 

 

إلا أن مفهوم توزيع الضرب على الجمع من الممكن أن يتم اكتشافه من قبل التلاميذ أنفسهم عن طريق النشاط التالي:

·       اختر عددين مختلفين غير واحد واثنين ولكونا 5 ، 3 على الذراع الأيمن من الميزان.

·       اختر عدداً من الأوزان وليكن في البداية 2.

·       قم بتمثيل العدد الأول والعدد الثاني على الطرف الأيمن من الميزان.

·       قم بوضع ثقلين (عدد الأوزان التي تم اختيارها) على كل عدد من العددين اللذين تم اختيارهما.

·       حاول إعادة التوازن إلى الطرف الأيسر بوضع أوزان على مشجب واحد فقط شريطة أن يكون عدد الأثقال في الطرف الأيسر مساو لعدد الأثقال التي تم اختيارها (2).

·       اكتب رقم المشجب الذي أعاد التوازن.

·       ما علاقة رقم المشجب بالعددين اللذين تم اختيارهما في هذا النشاط.

الشكل التالي يوضح الفكرة.

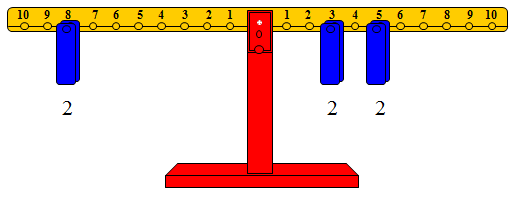
·       حيث تم اختيار العدد 5 والعدد 3 وتمثيلهما.

·       اختيار عدد الأثقال التي نضعها على كل عدد، وفي هذه الحالة عدد الأثقال هو 2.

·       تم وضع ثقلين على كل عدد من العددين.

·       تم إعادة التوازن بثقلين فقط (يمثلان عدد الأثقال) التي تم اختيارها على المشجب رقم 8 مما يعني أن: 2 × 5 + 2 × 3 = 2 × 8

وبتكرار النشاط على أعداد أخرى وبأوزان مختلفة يصل الطالب إلى أن:

أ ( ب + ج) = أ × ب + أ × ج

حيث أ تمثل عدد الأثقال التي نختارها ، ب ، ج يمثلان العددين.

أما عملية قسمة 56÷ 14 يمكن أن تتم على الميزان على النحو التالي:

·       تمثيل المقسوم (56) بوضع 5 أثقال على المشجب رقم 10 وثقل واحد على المشجب رقم 6 على الذراع الأيمن من الميزان.

ضع أثقال على العدد الذي يمثل المقسوم عليه (14) بوضع ثقل على المشجب رقم 10 وثقل على المشجب رقم 4 على الذراع الأيسر

تكرار الخطوة رقم (2) مرة أخرى وثالثة ورابعة إلى أن يصبح الميزان في وضع توازن مما يعني أن خارج القسمة يساوي 4، وهذا معناه أن 56 تساوي 4 × 14. وهذا يمكن إدراكه من معنى المعادلة: 56 = 4 × 14 = (4 × 4 ) + (4 × 10) كما يلي

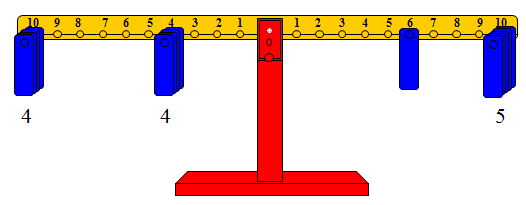
وبطريقة مشابهة يمكن تمثيل القسمة بباق (القسمة مع الباقي)، فقسمة 56 ÷ 9 تتم:

·       بتمثيل المقسوم (56) بوضع ثقل واحد على المشجب رقم 6 وخمسة أثقال على المشجب رقم عشرة في الذراع الأيمن من الميزان.

·       وضع أثقال على المشجب الذي يمثل المقسوم عليه.

·       في هذه الحالة 6 أثقال لا تكفي لإعادة التوازن، كما أن سبعة أثقال تكون أكثر من العدد المقسوم، وعليه نضع 6 أثقال على المشجب رقم تسعة (الذي يمثل المقسوم عليه) فيكون عدد الأثقال هو خارج القسمة (6).

·       نقوم بوضع ثقل واحد على الذراع الأيسر في أحد المشاجب، ورقم المشجب الذي يعيد الميزان إلى حالة التوازن هو العدد الذي يمثل الباقي، وفي هذه الحالة يكون الباقي 2.

قراءة خارج القسمة والباقي. والشكل التالي يوضح الفكرة

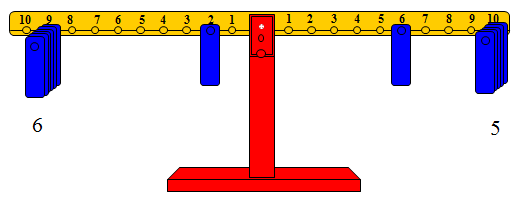
وعليه فإن المقسوم = 56

المقسوم عليه = 9

خارج القسم = 6

الباقي = 2

وهذا تجسيد للقسمة التقليدية حيث إن:

  

 

 

وبالطريقة نفسها يمكن تمثيل عملية القسمة التالية:

48 ÷ 5 = □

 

·       حيث يتم تمثيل المقسوم (48) على الذراع الأيمن بوضع ثقل واحد على المشجب رقم 8 وأربعة أثقال على المشجب رقم 10.

·       ثم تحديد مشجب المقسوم عليه (5) على الذراع الأيسر.

·       وضع 9 أثقال على المشجب الذي يمثل العدد المقسوم عليه وهي غير كافية، وعند وضع ثقل عاشر يكون ذلك أكبر من العدد المقسوم مما يعني الاكتفاء بوضع 9 أثقال على العدد المقسوم عليه، ووضع ثقل إضافي على مشجب آخر يعيد التوازن وهو المشجب رقم 3 وعليه فإن خارج القسمة هو 9 والباقي 3.

أي أن : 48 = (9 × 5 ) + 3

والشكل التالي يوضح الفكرة

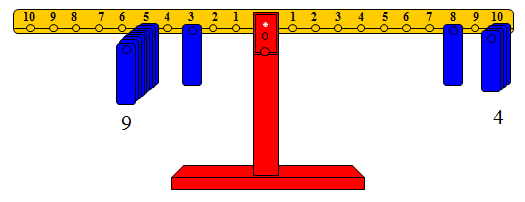
وبالطريقة نفسها يمكن إجراء عمليات القسمة المشابهة. وكما ذكرنا سابقاً فإن الهدف من استخدام الميزان ليس لإيجاد الحل، وإنما لتجسيد المفهوم الرياضي.

والشكل التالي يوضح علمية قسمة 50 ÷ 11 = □

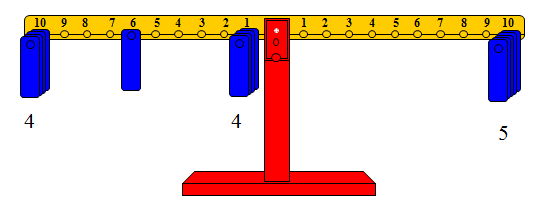
حيث تم تمثيل المقسوم (50) بوضع خمسة أثقال على المشجب رقم عشرة على الذراع الأيمن، وتحديد المشجب الذي يمثل المقسوم عليه (11) بوضع ثقل على المشجب رقم واحد، وثقل على المشجب رقم  10، وتكرار ذلك بوضع ثقل على كل المشجبين، وحيث إن 4 أثقال على كل منهما لا تكفي لإعادة التوازن، وأن خمسة أثقال أكبر من المقسوم، فإنه يجب بقاء 4 أثقال على كل منهما، والبحث عن مشجب نضع عليه ثقلاً واحداً يعيد التوازن.

وبالبحث نجد أنه المشجب رقم 6 مما يعني أن خارج القسمة 4 والباقي 6