3الضرب:

يمكن النظر إلى عملية الضرب على أنها عملية إيجاد حاصل الضرب عند معرفة العددين المضروبين.

فالعبارة: 6 × 2= □

يمكن قراءتها على أنها 6 ضرب 2 تساوي كم، وتعني أن عدد عناصر مجموعتين كل منهما مكون من 6 هو 2×6 ومن المفيد جداً تمثيل عملية الضرب في صورة مستطيل بعداه يمثلان العددين المضروبين، وعدد الوحدات المربعة التي يتكون منها ذلك المستطيل يمثل حاصل الضرب، ويمكن تمثيل العبارة 6 × 2 = □ بالمستطيل التالي

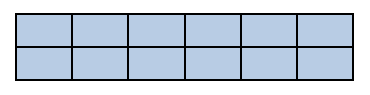
الذي يتكون من صفين كل صف 6 وحدات مربعة، حيث يمثل 6 ، 2 بعدي هذا المستطيل، في حين أن عدد الوحدات المربعة (المساحة) تساوي حاصل ضرب البعدين.

ويمكن استخدام المكعبات المتداخلة في تمثيل عملية الضرب بطريقة مشابهة، كما يمكن استخدام شبكة التربيع لتوضيح الفكرة نفسها. وبالرغم من أن ورق المربعات يمكن استخدامه للغرض نفسه، إلا أن تعامل الأطفال مع أشياء محسوسة Concrete Martials مثل المربعات البلاستيكية Square Tiles يكون أفضل. كما أن تجسيد المفهوم الواحد بأكثر من طريقة يعزز إدراك الطالب لهذا المفهوم.

وباستخدام الميزان فإن عملية ضرب 6 × 2 يمكن تنفيذها بوضع 6 أثقال على المشجب رقم 2 على الذراع الأيمن فيميل هذا الذراع، ويمكن إعادة التوازن بوضع عدد من الأوزان على المشاجب بالذراع الأيسر لتمثيل حاصل الضرب. ويمكن ذلك بوضع ثقل على المشجب رقم 10 وآخر على المشجب رقم 2، والشكل التالي يوضح ذلك

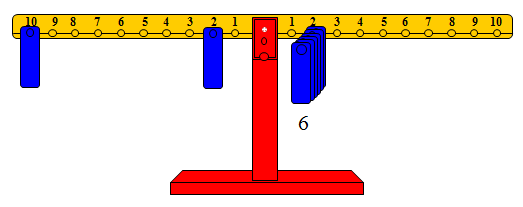
وبالطريقة نفسها يمكن ضرب أي عددين وإيجاد حاصل ضربهما.

الإبدال في الضرب:

إن عملية الضرب هي عملية إبداليه مما يعني أن: 6 × 2 = 2 × 6. وبالتعامل مع الميزان يصبح هذا المفهوم سهل الإدراك، وتمثل العملية بوضع ستة أثقال على المشجب رقم 2 على الذراع الأيمن ويتم إعادة التوازن عن طريق وضع ثقلين على المشجب رقم 6 على الذراع الأيسر. (العدد الأول يمثل عدد الأوزان والعدد الثاني يمثل رقم المشجب).

إن توحيد الأثقال وجعلها ذات وزن ثابت يسهل دراسة العمليات الحسابية ويجعل الاهتمام ينصب على بعد هذا الثقل من المركز، كما أن الاتفاق على جعل العدد الأول في علمية الضرب يمثل عدد الأوزان، في حين أن العدد الثاني يمثل رقم المشجب (البعد عن المركز) يساهم في تبسيط العملية، حيث يتعامل الطالب مع أدوات محسوسة وليس مع رموز وأرقام فعملية ضرب 4 × 3 = □ من الممكن ترجمتها إلى السؤال التالي:

كم ثقلاً ، وعلى أي المشاجب يمكن إعادة التوازن لأربعة أثقال موجودة على المشجب رقم 3 من الذراع الأيمن؟

  ولحل المعادلة يتبع الطالب الخطوات التالية:

·       يأخذ 4 اثقال ويضعها كلها على المشجب رقم 3 من الذراع الأيمن.

·       يحاول إعادة التوازن باستخدام مشجب واحد أولاً فيجد أنه لا يكفي لإعادة التوازن مما يضطره  لإضافة مشجب آخر وقد يصل عن طريقة المحاولة والخطأ إلى وضع ثقل على المشجب رقم 4 وآخر على رقم 8.

إلا أنه يجب لفت الانتباه إلى أنه في حالة كون ثقل واحد على مشجب واحد لا يكفي لإعادة التوازن فإن ذلك معناه أن حاصل الضرب أكبر من عشرة، ولتسهيل قراءة الناتج يجب وضع ثقل واحد على المشجب رقم عشرة أولاً، والبحث عن المشجب الآخر الذي نضع عليه الثقل الثاني ويعيد التوازن.

والشكل التالي يوضح الفكرة

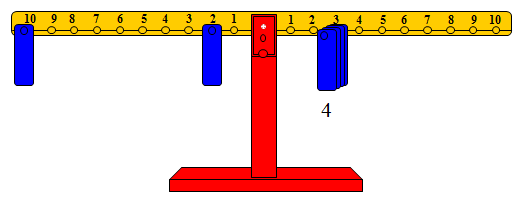
أي أن:  4×3=12

وبالطريقة نفسها يمكن إيجاد حاصل ضرب 4 × 8 حيث يضع الطالب 4 أثقال على المشجب رقم 8 من الذراع الأيمن فيميل الذراع ويتم البحث عن المشاجب التي تعيد التوازن إلى الذراع الأيسر إلا أنه يكتشف أن ثلاثة أثقال لا تكفي، وقد يستخدم ثقلاً رابعاً ويضعه على أحد المشاجب.. ويصل إلى الإجابة عن طريق المحاولة والخطأ. والشكل التالي يوضح إجابة أحد الطلاب

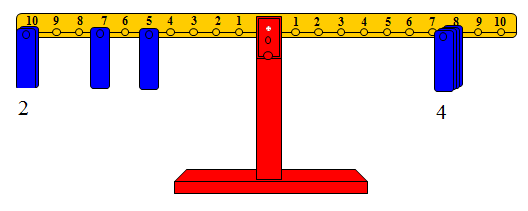
ومن الشكل نرى على الذراع الأيسر ثقلين على المشجب رقم عشرة وثقل على المشجب رقم 7 وثقل على المشجب رقم 5 وعند كتابة الإجابة وجد الطالب صعوبة، ولذلك (كما ذكرنا سابقاً) يجب وضع  الأثقال على المشجب رقم عشرة أولاً، فإذا اتضح أن إضافة ثقل جديد إلى الأثقال الموجودة على المشجب رقم عشرة أكبر من حاصل الضرب، عندها نبحث عن وضع الثقل الأخير على مشجب آخر مع إبقاء الأثقال السابقة على المشجب رقم عشرة، والهدف من كل ذلك هو تسهيل قراءة وكتابة الإجابة. والشكل التالي يوضح الفكرة

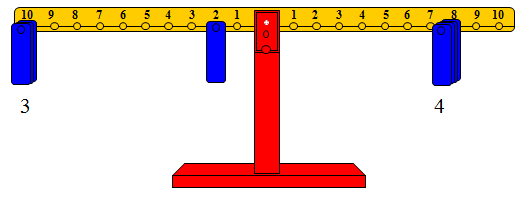
وعليه فإن 4 × 8 = 32

ثلاثة أثقال على المشجب رقم 3 يعني 3 عشرات أي 30

ثقل واحد على المشجب رقم 2 يعني 2.

2 + 30 = 32

وبالطريقة نفسها يمكن حل المعادلة 5 × 7 = □ بوضع أثقال على المشجب رقم 7 من الذراع الأيمن مقابل ثلاثة أثقال على المشجب رقم عشرة من الذراع الأيسر بالإضافة إلى ثقل واحد على المشجب رقم 5 من الذراع نفسه

 

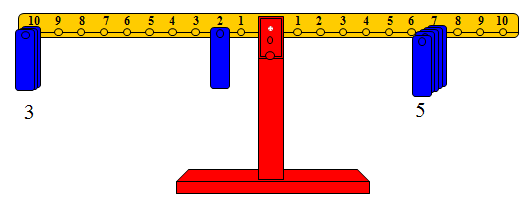
وعليه فإن □ = 35

جداول الضرب:

إن بناء جداول الضرب باستخدام الميزان يوضح أن عملية الضرب هي عملية جمع مكرر، فجدول 2 على سبيل المثال يمكن بناؤه على النحو التالي:

وضع ثقل واحد على المشجب رقم 2 على ذراع الميزان الأيمن وإعادة التوازن بوضع ثقل واحد على المشجب رقم 2 من الذراع الأيمن ليصبح لدينا ثقلين على هذا المشجب، ويتم إعادة التوازن بتحريك الثقل الموجود على الذراع الأيسر مسافتين بعيداً عن المركز إلى المشجب رقم 4 ويسجل الطفل 2 × 2 = 2 + 2 وتكرار العملية حيث نضيف في كل مرة ثقلاً واحداً على المشجب رقم 2 على الذراع الأيمن، وفي كل مرة نبعد الثقل الموجود على الطرف الأيسر مسافتين عن موقعه السابق بعيداً عن المركز.

إن عملية إضافة الأوزان (في كل مرة نضيف ثقلاً واحداً إلى المشجب رقم 2 على الذراع الأيمن) وعملية تحريك الثقل الموجود على الذراع الأيسر بعيداً عن المركز في كل مرة مسافتين يجب أن تسجل. وعندما يصل الطالب إلى 5 × 2 = 2 + 2 + 2 + 2 + 2 لا يمكن تحريك الثقل الموجود على الذراع الأيسر إلى مسافة أبعد لتمثيل 6× 2، وعليه يجب بقاء الثقل على المشجب رقم 10 وإضافة ثقل آخر في المشجب رقم 2 على الذراع الأيسر نفسه، وتتم عملية الإضافة للأوزان من جانب وتحريك الثقل من جانب آخر مع بقاء الثقل على المشجب رقم 10 (في كل مرة يصل فيها ثقل إلى هذا المشجب).

والشكل التالي يوضح :  6 × 2 = 12 = 2 + 2 + 2 + 2 + 2 + 2

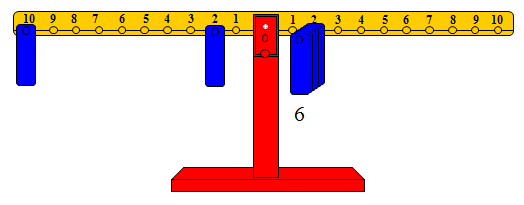
حيث يبقى الثقل على المشجب رقم 10 على الذراع الأيسر كما هو، وإضافة ثقل جديد على المشجب رقم 2 من الذراع الأيسر نفسه ليوازن مجموع الأثقال الستة على المشجب رقم 2 على الذراع الأيمن.

 والشكل التالي يوضح 7 × 2.

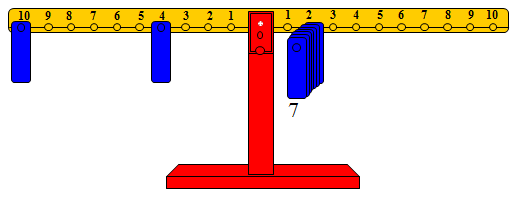
ثم نضيف ثقلاً على المشجب رقم 2 ليصبح عدد الوزان ثمانية ويتم إعادة التوازن بتحريك الوزن الذي كان سابقاً على المشجب رقم 4 إلى المشجب رقم 6 على الذراع الأيسر.

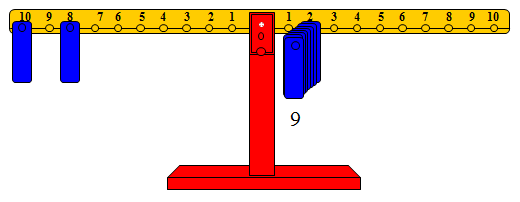
والشكل التالي يوضح 8×2

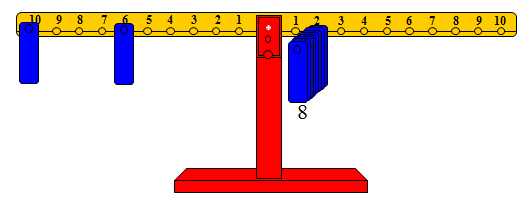
وعند إضافة ثقل على المشجب رقم 2 ليصبح عدد الأوزان تسعة يتم إعادة التوازن بتحريك الوزن الموجود على المشجب رقم 6 إلى المشجب رقم 8 على الذراع الأيسر. والشكل التالي يوضح 9 × 2.