2الطرح :

عملية الطرح تتلخص في إيجاد أحد العددين المجموعين عندما يعرف أحدهما وحاصل الجمع. فعلى سبيل المثال، إذا كان حاصل جمع عددين 9 وكان أحد العددين 5 فإن المسألة تصبح على النحو التالي:

5 + □ = 9

ومن الممكن قبول فكرة أن الطرح عملية عكسية للجمع. فالمعادلة 5 + □ = 9

يمكن تمثيلها على النحو التالي:

·       وضع ثقل على المشجب رقم 9 على ذراع الميزان الأيسر لتمثيل حاصل الجمع 9 مما يؤدي إلى انحراف الذراع استجابة للثقل الموضوع.

·       وضع ثقل على المشجب رقم 5 على الذراع الأيمن من الميزان لتمثيل العدد 5 وهذا يساعد في إعادة التوازن إلا أن الميزان لا يزال في حالة عدم اتزان.

والشكل التالي يوضح إعادة التوازن بإضافة ثقل على المشجب رقم 4 على الذراع الأيمن.

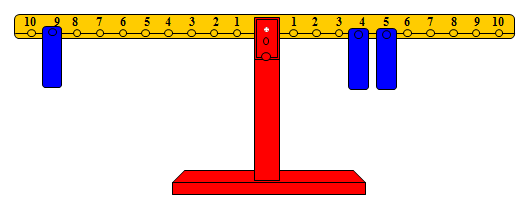
وتكمن المشكلة في إعادة التوازن إلى الوضع الطبيعي ويتم ذلك بوضع ثقل يمثل قيمة □ (العدد المجهول) في عملية الجمع: 5 + □ = 9

وهناك العديد من الطرق لحل المشكلة أحدها يتمثل في اتباع أسلوب المحاولة والخطأ، إلا أنه يجب ملاحظة أن عملية الطرح باستخدام الميزان تعني إيجاد الفرق تعرف باسم الجمع بالإكمال (Comptemenary addition) وهو أسلوب مهم في الحياة العامة، فالتاجر يستخدم هذا الأسلوب عند إعطائك الباقي، والطفل الذي يملك 5 ريالات ويرغب في شراء لعبة بتسعة ريالات يقوم بحساب الفرق بين ثمن اللعبة وما يملكه، ويعرف أنه بحاجة إلى أربعة ريالات زيادة عما لديه لشراء اللعبة.

وهناك طريقة أخرى تتلخص في حذف "طرح" العدد 5 من الطرفين دون الإخلال وهذه خبرة ملموسة للطفل. والمثال التالي يوضح الفكرة.

لنفرض أن طفلين على أحد طرفي المرجيحة (وليكن الطرف الأيمن) أحدهما على المشجب رقم 5 والآخر على مشجب مختلف يعادلان طفلاً واحداً على الطرف الأيسر من المرجيحة على المشجب رقم 9، فإذا أراد الطفل الموجود على المشجب رقم خمسة على الطرف الأيمن النزول من المرجيحة فإن التوازن يختل مما يدفع الطفل الموجود على الطرف الأيسر التقدم نحو المركز مسافة تعادل وزن الطفل الذي نزل من الطرف الأيمن، ويصبح موقعه الجديد على مسافة أقرب من المركز عما كان عليه سابقاً، إن هذا الوضع يمثل تماماً المعادلة: 5 + □ =9 فحذف الخمسة تعني نزول الطفل عن المرجيحة وهذا النزول يقابله تحرك الطفل الموجود على الطرف الأيسر (وهو الذي يمثل العدد 9) مسافة تعادل وزن الطفل الذي نزل ليصبح في الموقع الجديد قرب المركز (4).

 أي: 5 – 5 +  □ = 9 – 5

وعليه فإن  □ = 4

إن التعامل مع الميزان يعطي صورة واضحة للعلاقة بين الجمع والطرح. ومن الضروري أن يلاحظ الطلاب أن عملية الطرح هي العملية العكسية لعملية الجمع، وهذا المفهوم يصعب إدراكه بالتعامل مع الرموز فقط.

وكما هو الحال في الجمع يجب كتابة ما تم عمله في الطرح باستخدام الميزان في صورة معادلات رياضية. وعند جمع 2 + 4 = □ سلك بعض الأطفال سلوكاً مشابهاً لما تم شرحه في المثال الأخير، حيث وضع بعضهم ثقلاً واحداً على المشجب رقم 4 على الطرف الأيمن وثقلاً واحداً على المشجب رقم 4 على الطرف الأيسر على النحو التالي:

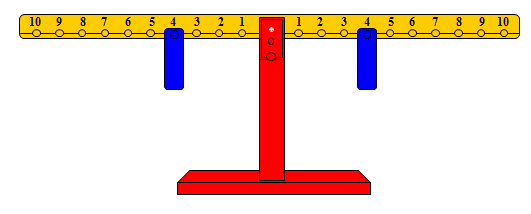
وعندما يرغبون في إضافة 2 إلى الطرف الأيمن يقومون بوضع ثق واحد على المشجب رقم 2 في ذلك الطرف ولكنهم يستخدمون أسلوباً آخر لإعادة التوازن عن طريق تحريك الثقل الموجود على المشجب رقم 4 على الذراع الأيسر مسافتين بعيداً عن المركز نحو اليسار فيصبح الثقل على المشجب رقم 6 ويتوازن ذراعا الميزان على النحو التالي:

 

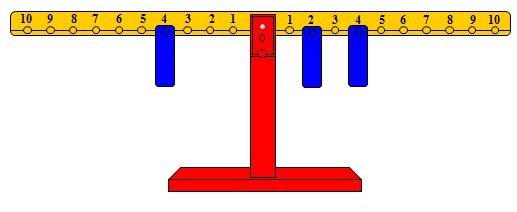
وهذا معناه أن الزيادة في أحد ذراعي الميزان يقابلها تحريك الثقل مسافة تعادل مقدار الزيادة بعيداً عن المحور وهذا هو المفهوم الحقيقي لقانون العزوم، إلا أن الأطفال يستخدمونه بالبديهة من خلال خبرتهم باللعب بالمرجيحة فهذا الموقف مشابه تماماً للمعادلة: 4 = 4، فطفل واحد على المشجب رقم 4 من الذراع الأيمن يعادل طفلاً واحداً على المشجب نفسه من الذراع الأيسر، فإذا أراد طفل ثالث الصعود إلى الطرف الأيمن على المشجب رقم 2 من المرجيحة مع الطفل الموجود من على المشجب رقم 4 من الذراع الأيمن ولم يكن هناك طفل رابع لإعادة التوازن فإن الطفل الموجود على الذراع الأيسر يتحرك بعيداً عن المركز لإعادة التوازن مسافة تعادل الثقل الجديد (2).

ومن خلال التعامل مع الميزان يدرك الطفل أن طرح عدد من أحد ذراعي الميزان يقابله إضافة ذلك العدد إلى الذراع الآخر من الميزان، ومن خلال خبرة الطالب المباشرة مع المرجيحة يدرك هذا المفهوم، كما يدرك أن إضافة أي ثقل إلى طرفي الميزان الذي يكون في حالة توازن لا يخل بالتوازن، فالمثال السابق: 5 + □ = 9 أدى إلى المعادلة التالية:

□ = 9 – 5 = 4

وعليه فإن المعادلات التي تحتوي على عملية طرح في أحد طرفيها تعني إضافة العدد المطروح إلى الطرف الآخر من المعادلة، ولا يمكن تمثيل عملية الطرح باستخدام الميزان إلا من خلال هذا الأسلوب.

وفي مرحلة متقدمة من الدراسة يعرف الطالب أن كل عملية جمع ينتج عنها عمليتي طرح.

فالمعادلة 5 + □ = 9   تنتج:

9 – 5 = □

9 -□ = 5

ولتمثيل عملية طرح 12 - □ = 9 نتبع الخطوات التالية:

·       نقوم بتمثيل العدد 12 بوضع ثقل واحد على المشجب رقم 2 وآخر على المشجب رقم عشرة على الطرف الأيمن من الميزان.

·       نقوم بتمثيل العدد 9 في لاطرف الأيسر وذلك بوضع ثقل واحد على الطرف الأيسر في المشجب رقم 9.

نبحث عن المشجب الذي نضع عنده ثقل في الطرف الأيسر (لوجود عملية طرح) لنعيد التوازن. والشكل التالي يوضح التوازن بإضافة ثقل على المشجب رقم 3

 

 

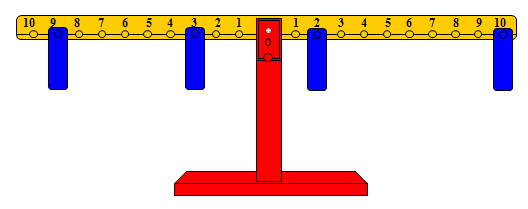
أما عمليات الطرح التي من النوع 15 – 9 = □ فيمكن تمثيلها بطريقة مشابهة على النحو التالي:

·       تمثيل العدد 15 بوضع ثقل على المشجب رقم 5 وآخر على رقم 10 من الذارع الأيمن.

·       تمثيل العدد 9 على الطرف الأيسر (لوجود عملية طرح) بوضع ثقل واحد على المشجب رقم 9.

·       محاولة البحث عن مشجب الطرف الأيسر لنضع عليه ثقلاً يعيد التوازن.

·       المشجب الذي يعيد التوازن هو الجواب.

والشكل التالي يوضح الفكرة:

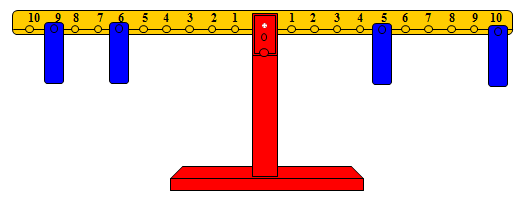
وفي هذه الحالة يكون □ = 6.

إن انحراف ذراع الميزان يسهل فكرة أن الأعداد المطلوب جمعها تساوي المجموع، ويجعلها فكرة مقبولة للطالب، ومن خلال الممارسة العملية لعمليات الجمع يلاحظ الطالب ويسجل ملاحظاته واكتشافه للقوانين.

ومن القوانين المتعلقة بالجمع التي يمكن ملاحظتها باستخدام الميزان ما يلي:

1.    أ + ب = ج  ، أ = (ج – ب)، ب = (ج – أ)

2.    أ + ب = ب + أ

3.    (أ + ب) + ج = أ + (ب + ج)= (أ + ج) + ب

مع ملاحظة أن القانون الأخير يتم تطبيقه عند جمع ثلاثة أعداد مختلفة.