الجمع بالميزان الحسابي المطور:

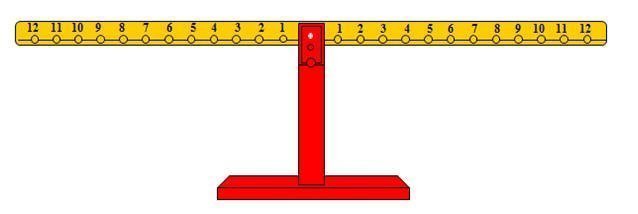
والشكل التالي يوضح صورة الميزان الحسابي المطور

ويمكن به دراسة عمليات حسابية أكثر حيث يمكن تمثيل العدد 12 بوضع ثقل واحد على المشجب رقم 12 ، وكذلك العدد 11 بوضع ثقل واحد على المشجب رقم 11 ،

كما يمكن دراسة الكسور مثل النصف، الثالث، الربع، السدس ، واحد على 12 بكل سهولة.

والشكل التالي يوضح عملية جمع 11 + 12 = □

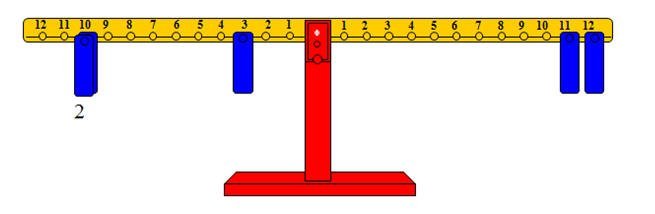
حيث تم تمثيل العدد 12 بوضع ثقل واحد على المشجب رقم 12 من الذراع الأيمن، ووضع ثقل واحد على المشجب رقم 11 من الذراع نفسه، وحيث إن وضع ثقلين على المشجب رقم عشرة

من الذراع الأيسر لا يكفيان لإعادة التوازن، وأن ثلاثة أثقال على ذلك المشجب أكبر من حاصل الجمع، لذا وجب إبقاء ثقلين على المشجب رقم عشرة ، ووضع ثقل واحد على المشجب الذي يعيد التوازن

وهو رقم 3.

وعليه فإن 12 + 11 = 23 .

وبالطريقة نفسها يمكن جمع (12 + 10 ) ، ( 12 + 9 ) ، (11 + 17 ) .

حيث تم تمثيل العدد 11 بوضع ثقل واحد على المشجب رقم 11  من الذراع الأيمن، وثقل واحد على المشجب رقم 9 ، بالإضافة إلى ثقل واحد على المشجب رقم 10 لتمثيل العدد 19،

والبحث عن المشجب أو المشجبين اللذين يعيدان التوازن على الذراع الأيسر. وحيث إن ثلاثة اثقال على المشجب رقم 10 تكفي لإعادة التوازن فإن □ = 30.

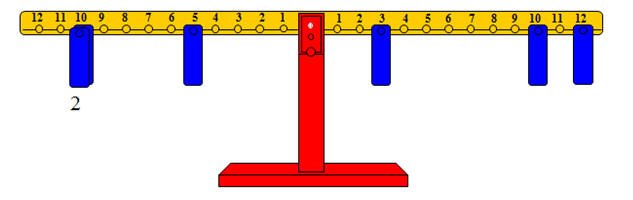
أما عملية جمع 12 + □ = 25 فيمكن تمثيلها على النحو التالي:

·       تمثيل العدد 12 على الذراع الأيمن.

·       تمثيل العدد 25 على الذراع الأيسر بوضع ثقل على المشجب رقم 5 وثقلين على المشجب رقم 10.

·       البحث عن المشجب الذي يعيد التوازن بوضع أثقال عليه، وحيث إن ثقلاً واحداً على المشجب رقم 10 من الذراع الأيمن لا يكفي لإعادة التوازن،

وأن ثقلين على ذلك المشجب يخل بالتوازن، وعليه يجب الإبقاء على ثقل واحد على المشجب رقم 10 والبحث عن مشجب آخر نضع عليه ثقلاً واحداً ويعيد التوازن،

وبالبحث نجد أنه المشجب رقم 3 ، وهذا معناه أن: □ = 3 + 10 = 13

والشكل التالي يوضح الفكرة

وبالطريقة نفسها يمكن إجراء عمليات الجمع التالية:

12 + □ = 25

11 + □ = 37

24 + □ = 31