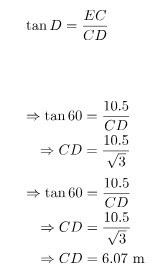Geometry in Maths - Definition, Shapes, Formulas, Examples & FAQs (geeksforgeeks.org)
Trigonometric Ratios - Definition, Formulas, Table, Examples, and FAQs (geeksforgeeks.org)
Mastering Mathematics: Essential Concepts, Formulas, and Problem-Solving
Techniques (geeksforgeeks.org)
Table of Content
What is Geometry?
Geometry is the study of different varieties of shapes, figures, and sizes. It
gives us knowledge about distances, angles, patterns, areas, and volumes of
shapes.
The principles of geometry depend on points, lines, angles, and planes. All the
geometrical shapes are based on these geometrical concepts.
The word Geometry is made up of two Ancient Greek words- ‘Geo’ means ‘Earth’ and
‘metron’ means ‘measurement’.
Geometry Definition in Maths
Geometry is a branch of mathematics that studies the properties, measurement,
and relationships of points, lines, angles, surfaces, and solids.
----
Plane Geometry
Plane geometry is concerned with the shapes that can be drawn on paper.
Euclidean geometry involves the study of plane geometry.
A 2D surface spread infinitely in both directions is referred to as a plane. The
basic components of the plane are:
-
Points – A point is
the no-dimensional fundamental unit of geometry.
-
Lines – A line is
a straight path on a plane that extends in both directions with no
endpoints.
-
Angles – Plane geometry consists of lines, circles, and triangles of two
dimensions. Plane geometry is another name for two-dimensional geometry.
Important Points:
-
Collinear points are the ones that lie on the same line.
-
A line segment is part of a line that has two endpoints and is finite in
length.
-
A ray is
a line segment that extends indefinitely in one direction. A line has no
endpoints.
-
Line, line segment, and ray are different from each other.
.png)
Plane Geometry
All two-dimensional figures have only two dimensions: length and width. Plane
figures consist of squares, triangles, rectangles, circles, and so on.
Angles in Geometry
In planar geometry, an angle is formed when two rays intersect, called the sides
of the angle, and share a common endpoint known as the vertex of the angle.
There are majorly four types of angles
-
Acute Angle- An
Angle between 0 to 90 degrees.
-
Obtuse Angle–
An angle more than 90 degrees but less than 180 degrees.
-
Right Angle–
An angle of 90 degrees.
-
Straight Angle–
An angle of 180 degrees is a straight line.
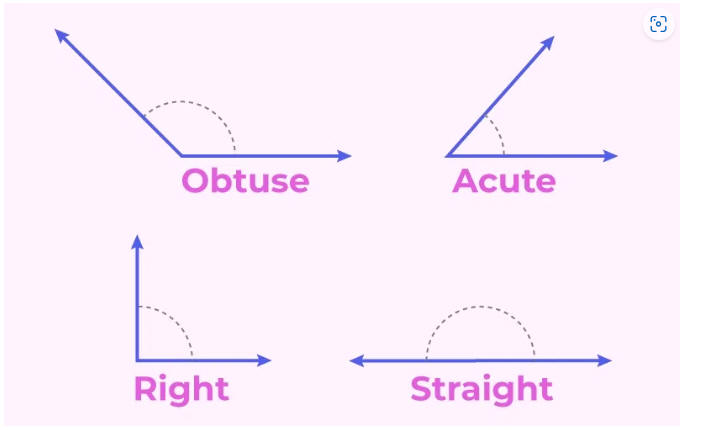
Angles in Geometry
You can find similar topics discussed in depth in the below articles.
-
Lines and Angles
-
Pairs of Angles
The article with the name “Applications of Trigonometry”
as the name suggests will explore the application of trigonometry in
the real world. Trigonometry has a lot of real-life applications of trigonometry
such as in astronomy to calculate the distance between planets and stars. Other
than that, one application of trigonometry is the calculation of the height and
distance of various objects in the real world. In this article, we’ll solve some
problems based on the concepts such as angle of elevation, line of sight, angle
of depression, etc. So, let’s learn about the Applications of Trigonometry.
Triangle Inequality is
the relation between the sides and angles of triangles which helps us
understand the properties and solutions related to triangles. Triangles are
the most fundamental geometric shape as we can’t make any closed shape with
two or one side. Triangles consist of three sides, three angles, and three
vertices.
The construction possibility of a triangle based on its side is given by the
theorem named “Triangle
Inequality Theorem.” The Triangle
Inequality Theorem states
the inequality relation between the triangle’s three sides. In this article,
we will explore the Triangle Inequality Theorem and some of its applications
as well as the other various inequalities related to the sides and angles of
triangles.
In this article, we’ll delve into the concept of triangle
inequality, triangle inequality theorem, its significance, and its practical
applications.
What is Triangle Inequality?
Triangle Inequality is
a fundamental geometric principle that plays a vital role in various
mathematical and real-world applications. It lays the foundation for
understanding relationships between the sides of a triangle, contributing to
fields such as geometry, physics, and computer science.
Triangle Inequality Theorem
Triangle Inequality Theorem states
that “the sum of the length of any two sides of a triangle must be greater
than the length of the third side.” If the sides of a triangle are a, b, and
c then the Triangle
Inequality Theorem
can be represented mathematically as:
-
a + b > c,
-
b + c > a,
-
c + a > b
Triangle Inequality Proof
In this section, we will learn the proof of the triangle inequality theorem.
To prove the theorem, assume there is a triangle ABC in which side AB is
produced to D and CD is joined.
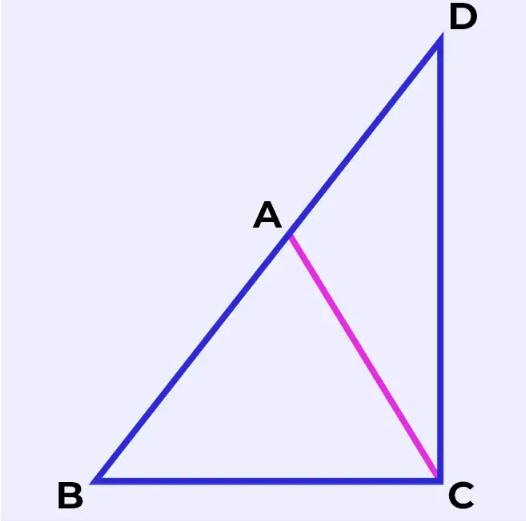
Notice that the side BA of Δ ABC has been produced to a point D such
that AD = AC. Now, since ∠BCD > ∠BDC.
By the properties mentioned above, we can conclude that BD > BC.
We know that, BD = BA + AD
So, BA + AD > BC
= BA + AC > BC
So, this proved sum of two sides triangle is always greater than the
other side.
Let’s see an example based on Triangle Inequality Theorem to understand its
concept more clearly.
Example: D is a point on side BC of triangle ABC such that AD = DC. Show
that AB > BD.
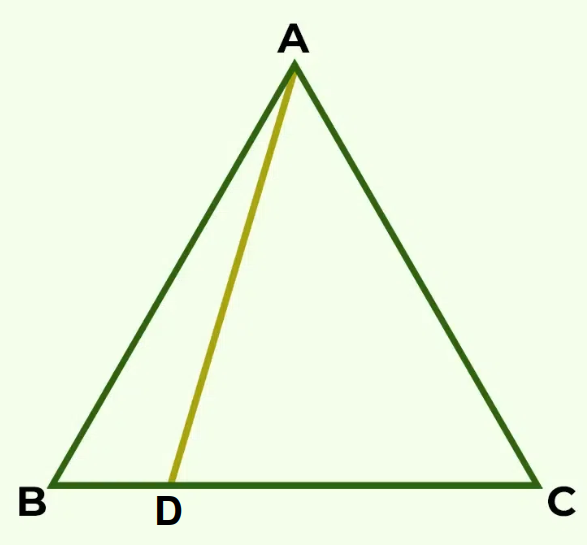
Solution:
In triangle DAC,
AD = AC,
∠ADC = ∠ACD (Angles opposite to equal sides)
∠ ADC is an exterior angle for ΔABD.
∠ ADC > ∠ ABD
⇒ ∠ ACB > ∠ ABC
⇒ AB > AC (Side opposite to larger angle in Δ ABC)
⇒ AB > AD (AD = AC)
What is Trigonometry
Trigonometry is the branch of mathematics that deals with the study of
relationships between the sides and angles of a triangle. In trigonometry, there
are six trigonometry ratios such as sine, cosine, tan, sec, cosec, and cot.
Before understanding the application of Trigonometry, we need to understand some
basic terms such as
-
Line of Sight
-
Angle of Elevation
-
Angle of Depression
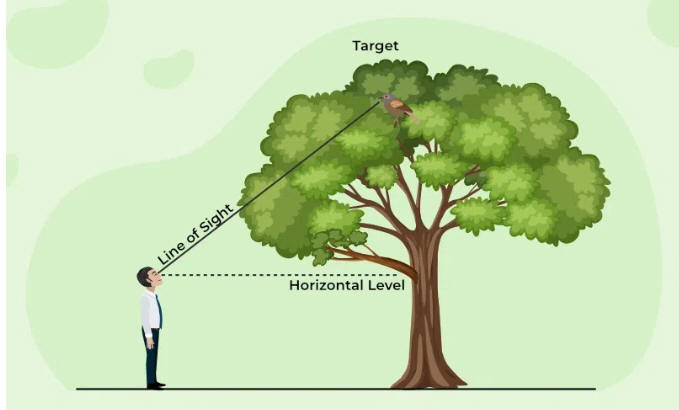
Line of Sight
Consider a person looking at the top of the tree as in the below figure:
In this figure, the line DE drawn from the eye of the boy to the top of the tree
is called a Line
of Sight.
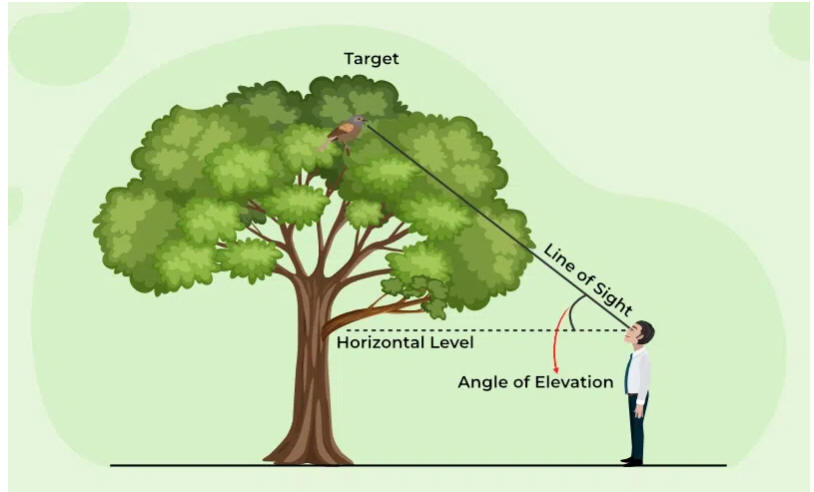
Angle of Elevation
Consider a person looking at the top of the tree as in the below figure:
The angle between the line of sight and the horizontal level at the eye of the
boy, ΔCDA or ∠D, is called the angle
of elevation.
When we measure the angle of elevation, the observer should raise their head and
look above the horizontal level.
Here if one wants to calculate the height of the tower without actually
measuring it then what and how much information is required? The following
detail is necessary to find out the height of the tower without measuring it;
-
Distance, AB or CD, between the tower and the point where the boy standing.
-
The angle of elevation, ∠EDC, of the top of the tower.
-
The height of the boy DA.
In ΔCDE, the known ∠D is the opposite of the side CE, and it is known that the
side CD. So here is the trigonometry ratio, that can be used to apply all these
three quantities. Determine tan D or cot D as their ratio involves CD and CE.
While calculating the length of the tower or any other object, one should keep
in mind the length of the boy to add in the result get from the trigonometry
ratio. By the following example, this concept will more clear.
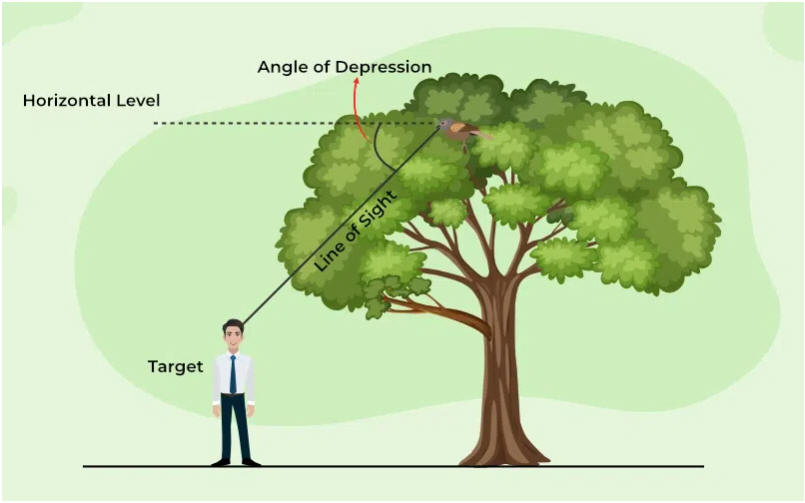
Angle of Depression
Now consider a situation as in given figure 4, a person is looking towards a
ball from a balcony. Its line of sight is below the horizontal level. The angle
between the line of sight and the horizontal level is called the angle
of depression.
Thus, the angle of depression of the point on the object is the angle between
the horizontal level and line of sight when the point is the below horizontal
level
In the above figure, the person at point C, is looking towards the ball at B. CB
is the line of sight and AC is the height of the balcony.
In ΔBCD, ∠BCD is the angle of depression of point B. Here is the height of the
balcony AC = BD and the distance of the ball from the ground foot of the
building AB = CD. According to the given data, the trigonometry ratio can be
used as it can involve both known and unknown quantities.
Trigonometry Applications in Real Life
There are various applications of trigonometry and some of the common
applications of trigonometry are,
Trigonometry to Measure Height
The basic use or application of trigonometry is the measure of height. We use
the concept of trigonometry to measure the height and distance between two
objects by measuring the angles between these objects. We can easily find the
height of an object if we know the distance between any point and the foot of
the building and the angle of elevation or the depression of that point from the
building.
Trigonometry in Aviation
We use trigonometry in aviation for measuring the height and speed of any flying
objects such as Airplanes and missiles. The exact position of the airplane and
other flying objects can be measured if we are given its height and the angle of
elevation.
Trigonometry in Navigation
Trigonometry is widely used in the navigation of ships and others we can easily
find the position of our ship in the ocean with the help of stars and the
knowledge of trigonometry and angles.
Trigonometry in Astronomy
Trigonometry is widely used in astronomy to find the distances and positions of
the stars and other heavenly bodies. We can measure the angle of various
heavenly bodies from the Earth by knowing the time taken by the light from that
body to reach the Earth’s surface and the speed of light we can find its
position in space using trigonometry.
Other Uses of Trigonometry
The other uses of trigonometry are discussed below,
-
It is used in criminology to study crime scenes.
-
It is used by marine biologists to study the depth of oceans and others.
-
It is used to study waves and their properties.
Read More,
Sample Problems on Applications of Trigonometry
Problem 1: A pole stands vertically on the plane. From a point on the plane,
which is 12 m away from the foot of the pole, the angle of elevation of the top
of the pole is 30° Find the height of the pole.
Solution:
First, draw a simple diagram of the given problem as below:
In this figure, BC represents the height of the electric pole and ∠CAB or ∠A
represents the angle of the elevation of the top of the tower. In ΔABC, ∠CAB
is the right angle and AB = 12 m. In ΔABC, CB is needed to be determined
i.e. the height of the pole.
To solve the given problem, use trigonometry ratio tan A or cot A as they
involve given sides in ratios.
Now,
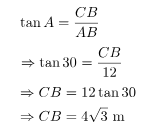
Hence, the height of the poll is 4√3.
Problem 2: A boy sees two clouds from a certain point. The angle of the
elevation of the clouds are 30° and 45°. If the height of the clouds from the ground
surface is the same and the distance between the clouds is 300 m then find out
the height of the cloud.
Solution:
First, draw a simple diagram of the given problem as below.
In this figure, CE and BD represents the height of the clouds and ∠DAB and ∠EAC
represents the angle of the elevation of the clouds at point A. In ΔABD, ∠DBA
is the right angle, if the height of cloud BD is h then using trigonometry
ratio tan A
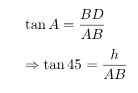
⇒ AB = h (Since, tan 45° = 1)
In ΔACE, ∠ACE is the right angle, if the height of cloud CE is h then using
trigonometry ratio as:

⇒ AC = h√3
From the above figure 4,
AC = AB + BC
Given: BC = 300.
Therefore,
h√3 = h + 300

Hence, the height of the cloud is 410.96 m.
Problem 3: The angle of elevation of the bird, who was sitting on a tree, from
a point on the ground, which is 60 m away from the foot of the tree, is 60°.
Find the height of the tree. (Take √3 = 1.73).
Solution:
First draw
a simple diagram of the given problem as below:
In above figure, AB represents the distance between the ground point and
foot of the tree, i.e. 60 m. BC is the height of the tree, let’s assume h.
In ΔABC, ∠ABC is the right angle, and the angle of the elevation is ∠B i.e.
60°.
Using trigonometry ratio tan A,
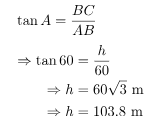
Hence, the height of the tree is 103.8 m.
Problem 4: The angle of depression of a bike, standing in a park, from the top
of a 45 m high building, is 30°. What is the distance of the bike from the base
of the building (in m)?
Solution:
Below is a simple diagram of the given problem.
In above figure, AB represents the distance between the base of the building
and the bike. AC is the height of the building, i.e. 45 m.
In ΔBCD, ∠BCD is the right angle and the angle of the depression is ∠C
i.e. 30°. Using trigonometry ratio tan C in ΔBCD.
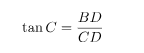
Here AC = BD and AB = CD.
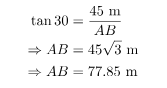
Hence, the distance between the base of building and the bike is 77.85 m.
Problem 5: An electrician needs to repair an electric fault to solve the power
supply issue in a village. The height of the electric pole, on which the fault
exists, is 7 m. He wants to reach a point below 1.5 m from the top of the pole
to repair the fault. What length of the ladder he should use to reach the
required position if the ladder is inclined at 60° to the horizontal? Also, find
how far the ladder he should place from the foot of the pole (Take √3 = 1.73).
Solution:
First, Draw a basic diagram of the given problem as below:
In this figure, BC is the ladder, AD is the total length of the pole, Point
C is the where electrician wants to reach.
As given CD = 1.5 m and AD = 7 m.
Therefore,
AC = AD – CD
⇒ AC = 7 – 1.5 m
⇒ AC = 5.5 m
In ΔABC, ∠B is 60° and ∠A is right angle,
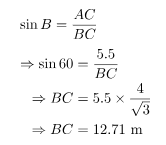
And, in ΔABC,

Hence, the length of the ladder BC is 12.71 m and the distance between
ladder and foot of the pole AB is 3.17 m.
Problem 6: The angle of elevation of a cloud from a point, which is somewhere on
the surface of the water of a lake, is 30°. The angle of depression of the
shadow of a cloud
in the water of the lake from the same point is 60°. If the height of the cloud
is 75 m then find the depth of the shadow. (Take √3 = 1.73).
Solution:
First, draw a basic diagram of the given problem as below:
In this figure, AB is the water surface of the lake. Points C and D
represent the cloud and its shadow respectively. ∠ABC and ∠ABD are the right
angles. BC is the height of the cloud, i.e. 75 m and BD is the depth of the
shadow. ∠BAC and ∠BAD are the angle of elevation and the angle of the
depression, i.e. 30° and 60°.
In ΔABC,

Now in ΔABD,
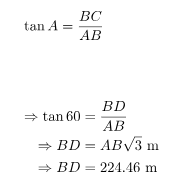
Hence, the depth of the shadow is 224.46 m.
Problem 7: Consider the following diagram:
If the √ACB is the right angle find the AB and CD (Take √3 = 1.73).
Solution:
In ΔACD, use the trigonometry ratio sin A,
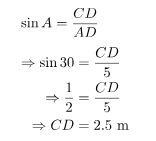
And,

 ⇒ BC = CD = 2.5 m
⇒ BC = CD = 2.5 m
From the given figure:
AC = AB + BC
⇒ AB = 4.33 m – 2.5 m
⇒ AB =1.83 m
Hence, AB = 1.83 m and CD = 2.5 m.
Problem 8: A 1.5 m tall boy is looking toward two buildings. Both buildings have
a height of 12 m. The elevation angle of the top of the buildings is 45° and
60°. Find the distance between the two buildings and the distance of the boy
from the near building.
Solution:
A simple diagram of the given problem is drawn below
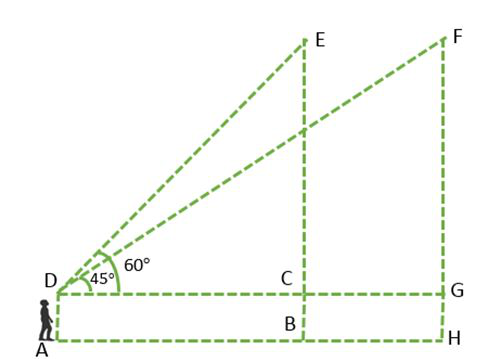
Figure 6
In the above figure, CB and GH represent the two buildings, CG is the
distance between the two buildings, CD and GD is the distance between the
boy and foot of the buildings of EB and FH respectively.
In ΔCDE and ΔFDG,
EC = FG = EB – AD (Since, AD = CB = GH)
⇒ EC = FG = 12 m – 1.5 m
⇒ EC = FG = 10.5 m
In ΔCDE, ∠CDE is equal to  and
∠DCE is the right angle.
and
∠DCE is the right angle.
In ΔFDG, ∠FDG is  and ∠FGD
is right angle.
and ∠FGD
is right angle.
The distance between the buildings is:
CG = GD – CD
⇒ CG = 10.5 m – 6.07 m
⇒ CG = 4.43 m
Hence, the distance between the buildings CG is 4.43 m and the distance
between the boy and the foot of the near building CD is 6.07 m.
FAQs on Applications of Trigonometry
Q1: Define Trigonometry.
Answer:
Trigonometry is a branch of mathematics that deals with the relationships
between the sides and angles of triangles.
Q2: What are Basic Trigonometric Ratios?
Answer:
The basic trigonometric ratios are sine, cosine, and tangent. These ratios
relate the sides of a right triangle to its angles.
Q3: What is the Sine Ratio?
Answer:
The sine ratio is defined as the ratio of the length of the side opposite an
angle to the length of the hypotenuse in a right triangle.
Q4: What is the Cosine Ratio?
Answer:
The cosine ratio is defined as the ratio of the length of the adjacent side
to the length of the hypotenuse in a right triangle.
Q5: What is the Tangent Ratio?
Answer:
The tangent ratio is defined as the ratio of the length of the side opposite
an angle to the length of the adjacent side in a right triangle.
Q6: What are the Reciprocal Trigonometric Ratios?
Answer:
The reciprocal trigonometric ratios are cosecant, secant, and cotangent.
These ratios are the reciprocals of the sine, cosine, and tangent ratios,
respectively.
Q7: What are some Real-life Applications of Trigonometry?
Answer:
Trigonometry has many practical applications in fields such as engineering,
architecture, physics, and navigation. It can be used to calculate
distances, angles, heights, and other geometric quantities in real-world
situations.
Here's a complete roadmap for you to become a developer:
Learn DSA -> Master Frontend/Backend/Full Stack -> Build Projects -> Keep
Applying to Jobs
And why go anywhere else when our DSA
to Development: Coding Guide helps you do this in a single
program! Apply now to our DSA
to Development Program and our counsellors will connect with you for
further guidance & support.



.png)




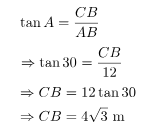

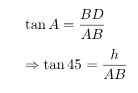


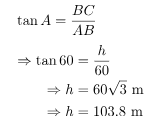

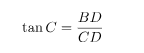
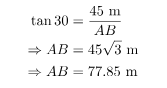

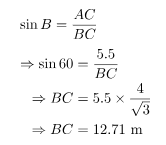



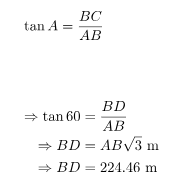

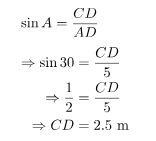

 ⇒ BC = CD = 2.5 m
⇒ BC = CD = 2.5 m