النتيجة: العددان هما 9 و16.
الاستراتيجية (Strategy) الطريقة (Method) الأسلوب( Style)
أولاً:
الاستراتيجية (Strategy)
التعريف:
الاستراتيجية :
هي خطة عامة شاملة تُستخدم لتحقيق هدف محدد في التعلم أو لحل مشكلة. تركّز على تسلسل الخطوات الكبرى التي تقود المتعلم إلى الهدف، وتجمع بين التفكير والتنظيم
والتخطيط.
هي الإطار العام الذي يوجّه المعلم لاختيار الأنشطة والوسائل المناسبة لتحقيق أهداف الدرس.
مثال:
استراتيجية حل المشكلات في الرياضيات، والتي تمر بخطوات:
فهم المشكلة
وضع خطة للحل
تنفيذ الخطة
التحقق من الحل
فهي تحدد مسار التفكير الكامل من البداية حتى التحقق من النتيجة.
ثانيًا:
الطريقة (Method)
التعريف:
الطريقة هي الإجراء المنظم والخطوات التفصيلية التي يتبعها المعلم أو المتعلم لتنفيذ جزء من الاستراتيجية. بمعنى أنها تحدد كيف نُنفّذ الخطة العامة عمليًا داخل الصف.
في التدريس:
هي الكيفية التي يُقدَّم بها المحتوى التعليمي، أو تُنظَّم بها الأنشطة للوصول إلى هدف معين.
مثال:
داخل استراتيجية حل المشكلات، يمكن اختيار طريقة الجدول أو طريقة المعادلات أو طريقة التمثيل بالرسم.
مثلاً:
في مسألة “مجموع عددين 20 والفرق بينهما 4”، يمكن حلها بطريقة الجدول من خلال تجربة القيم المختلفة حتى الوصول إلى الحل الصحيح.
إذن الطريقة هنا هي “الأداة العملية” لتنفيذ ما ترسمه الاستراتيجية.
ثالثًا:
الأسلوب (Style)
التعريف:
الأسلوب هو الطابع الشخصي أو النمط الخاص في تطبيق الطريقة أو الاستراتيجية. ويمثل الجانب الشخصي والفني في عرض الدرس، ويتأثر بشخصية المعلم وخبرته
وطبيعة الموقف التعليمي.
في التدريس:
هو الكيفية التي يتفاعل بها المعلم مع طلابه أثناء تنفيذ الطريقة، مثل:
أسلوب التشويق
أسلوب التعلم القائم على المواقف الواقعية
مثال:
في طريقة “التمثيل بالرسم”، قد يستخدم معلم أسلوب الحوار فيطرح أسئلة أثناء الرسم، بينما يستخدم آخر أسلوب العرض المباشر ويشرح بنفسه دون تفاعل كبير.
فالأسلوب لا يغيّر جوهر الطريقة، لكنه يغيّر طريقة عرضها وتفاعل الطلاب معها.
الفروق بين المصطلحات الثلاثة:
المقارنة الاستراتيجية الطريقة الأسلوب المفهوم خطة عامة شاملة لتحقيق هدف أو حل مشكلة خطوات عملية لتنفيذ جزء من الاستراتيجية النمط الشخصي في تنفيذ الطريقة النطاق أوسع وأشمل ضيق (جزء من الاستراتيجية) شخصي وفني الوظيفة تحدد كيف نفكر ونخطط تحدد كيف نعمل وننفذ تحدد كيف نعرض ونتفاعل التركيز على تنظيم الموقف التعليمي ككل على إجراءات التعليم المحددة على أداء المعلم وطريقته الخاصة المسؤول المعلم والمتعلم معًا المعلم غالبًا المعلم بالدرجة الأولى مثال في الرياضيات استراتيجية حل المشكلات طريقة الجدول أو المعادلة أسلوب الحوار أو التشويق
مثال تطبيقي يوضح الفرق:
أراد المعلم تعليم الطلاب كيفية حل مسألة تتعلق بعدد من الكتب والأقلام.
- استخدم استراتيجية حل المشكلات (خطوات: فهم – خطة – تنفيذ – تحقق).
- اختار طريقة الحواروالمناقشة لتجريب القيم المختلفة.
- قدّم الدرس باستخدام أسلوب التشويق لجعل الطلاب متفاعلين.
استراتيجية التخمين والتحقق (Guess and Check)
المفهوم:هي استراتيجية لحل المسائل التي يصعب حلها مباشرة، حيث نقوم بتخمين إجابة ثم التحقق من صحتها، ونكرر العملية حتى نصل إلى الحل الصحيح.
خطوات التطبيق:
1. فهم المسألة وتحديد المعطيات والمطلوب
2. عمل تخمين منطقي أولي
3. التحقق من صحة التخمين
4. تعديل التخمين بناءً على نتائج التحقق
5. الاستمرار حتى الوصول للحل الصحيح
هي استراتيجية مباشرة تعتمد على البدء بتخمين أولي لحل المشكلة، ثم التحقق من صحة هذا التخمين بتطبيقه على شروط المشكلة.إذا لم يكن صحيحًا، نعدل تخميننا بناءً على نتيجة التحقق ونكرر العملية حتى نصل إلى الحل الصحيح.
كيفية التطبيق:
1. التخمين: اقترح تخمينًا منطقيًا للحل. لا يجب أن يكون عشوائيًا تمامًا؛ فكّر في الأرقام أو القيم التي تبدو معقولة في سياق المشكلة.
2. التحقق: عوّض بتخمينك في معطيات وشروط المشكلة الأصلية (عادةً في المعادلة أو العلاقات المذكورة).
3. التعديل: حلل نتيجة التحقق. هل كان تخمينك مرتفعًا جدًا أم منخفضًا جدًا؟ استخدم هذه المعلومة لتقديم تخمين أفضل وأكثر دقة.
4. التكرار: استمر في هذه الدورة (تخمين ← تحقق ← تعديل) حتى تجد الحل الذي يحقق جميع شروط المشكلة.
متى نستخدمها؟
· عندما لا تكون هناك علاقة واضحة مباشرة بين المعطيات والمطلوب.
· عندما تكون المشكلة معقدة بعض الشيء ولكن لديها عدد محدود من الحلول المحتملة.
· للمساعدة في فهم بنية المشكلة بشكل أفضل.
· عندما تكون المعادلات صعبة الحل جبريًا.
مثال توضيحي:
"متى يصبح عمر الأب ضعف عمر ابنه إذا كان عمر الأب الآن 40 سنة وعمر ابنه 10 سنوات؟"
· التخمين الأول: بعد 10 سنوات. عمرالأب = 50،عمر الابن = 2050 ليس ضعف عمر الابن لأن 50 قسمة 20 = 2.5 (النتيجة أكبر من 2، إذن التخمين كبير).
· التخمين الثاني: بعد 5 سنوات. عمرالأب = 45،عمرالابن = 1545 ÷ 15 = 3 (النتيجة أكبر من 2، لكنها أفضل).
· التخمين الثالث: بعد 20 سنة. عمرالأب = 60، عمر الابن = 3060 ÷ 30 = 2 (هذا هو الحل الصحيح).
المميزات: بسيطة وبديهية، لا تتطلب معرفة متقدمة بالجبر.العيوب: قد تستغرق وقتًا طويلاً إذا كانت التخمينات غير منظمة.
استراتيجية التخمين والتحقق (Guess and Check)
التعريف:
هي استراتيجية استكشافية تعتمد على التفكير التكراري، حيث يبدأ الحل بتخمين أولي ثم اختبار هذا التخمين(التقدير) مقابل شروط المسألة،مع تعديل متتالي حتى الوصول للحل الأمثل.
الأسس النظرية
· تعتمد على التعلم من الأخطاء· تنمي مهارة التقدير والحدس الرياضي
· تطور قدرة التكيف مع التغذية الراجعة
الخطوات التفصيلية
المرحلة الأولى: التحضير
1. تحليل المسألة بعمق· تحديد جميع المعطيات والشروط
· فهم العلاقات بين المتغيرات
· تحديد الهدف النهائي بوضوح
2. تخطيط استراتيجية التخمين
· تحديد نطاق التخمينات الممكنة
· اختيار نقطة بداية منطقية
· وضع معايير لتقييم التخمينات
المرحلة الثانية: التنفيذ التكراري
1. التخمين المدروس· اختيار قيمة بناءً على التحليل الأولي
· توثيق سبب اختيار هذا التخمين
2. التحليل الشامل
· تطبيق جميع شروط المسألة على التخمين
· حساب الانحراف عن الشروط المطلوبة
· تقييم مدى قرب التخمين من الحل
3. التعديل المستنير
· تحليل أسباب الخطأ في التخمين السابق
· تحديد اتجاه وكمية التعديل المطلوبة
· اختيار تخمين جديد أكثر دقة
المرحلة الثالثة: التقويم
1. التحقق النهائي· اختبار الحل النهائي ضد جميع الشروط
· التأكد من شمولية الحل
· توثيق عملية الحل كاملة
مميزات الاستراتيجية
· تنمي التفكير النقدي· مرنة وتناسب مسائل متنوعة
· تشجع على التجريب والتعلم
· مناسبة للمبتدئين في حل المسائل
عيوب الاستراتيجية
· قد تستغرق وقتاً طويلاً· غير مضمونة الوصول للحل
· قد تؤدي إلى إحباط مع المسائل المعقدة
استراتيجية بناء الجدول (Make a Table)
التعريف
هي استراتيجية تنظيمية منهجية تعتمد على تمثيل البيانات في هيكل جدولي يسمح بملاحظة الأنماط والعلاقات بشكل منهجي.
الأسس النظرية:· تعتمد على التنظيم المنطقي للبيانات
· تستخدم الاستقصاء الشامل للاحتمالات
· تنمي مهارة التحليل البصري للأنماط
الخطوات التفصيلية:
المرحلة الأولى: التصميم
1. تحليل المتغيرات· تحديد المتغيرات المستقلة والتابعة
· تحليل العلاقات بين المتغيرات
· تحديد نطاق القيم الممكنة
2. هيكلة الجدول· تصميم الأعمدة والصفوف
· تحديد عناوين مناسبة
· تخطيط تسلسل ملء البيانات
المرحلة الثانية: البناء
1. الملء المنهجي· اتباع تسلسل منطقي في الملء
· ضمان شمولية جميع الاحتمالات
· الحفاظ على التنظيم والدقة
2. التحليل المتزامن· مراقبة الأنماط أثناء الملء
· تسجيل الملاحظات والاستنتاجات
· تحديد الاتجاهات العامة
المرحلة الثالثة: الاستنتاج
1. التحليل الشامل· دراسة العلاقات بين الأعمدة
· تحديد الأنماط والتكرارات
· استخلاص القواعد العامة
2. استخراج الحل· تطبيق شروط المسألة على البيانات
· تحديد الصفوف التي تحقق الشروط
· التحقق من صحة النتائج
مميزات الاستراتيجية
· شمولية تغطية جميع الاحتمالات· تنظيم البيانات بشكل واضح
· تسهيل ملاحظة الأنماط
· مناسبة للمسائل المعقدة متعددة المتغيرات
عيوب الاستراتيجية
· قد تكون مملة مع البيانات الكبيرة· تتطلب وقتاً في التصميم والملء
· قد تكون غير عملية مع نطاقات كبيرة
استراتيجية بناء جدول (Make a Table)
هي استراتيجية منهجية تنظيمية. نقوم بإنشاء جدول لتنظيم البيانات بشكل منظم، مما يسمح لنا برؤية الأنماط والعلاقات بين المتغيرات بسهولة،وبالتالي تحديد الحل.
كيفية التطبيق:
1. تحديد المتغيرات: حدد ما هي الأعمدة التي ستحتاجها في جدولك (على سبيل المثال، عدد المرات، القيمة الأولى، القيمة الثانية، النتيجة).2. بناء الجدول: أنشئ الجدول وابدأ في ملء البيانات بشكل منهجي، غالبًا بزيادات ثابتة (مثل 1، 2، 3... أو 5، 10، 15...).
3. التحليل والبحث عن النمط: ابحث عن علاقة أو نمط في البيانات المدخلة. الهدف هو العثور على الصف الذي تحقق فيه جميع الشروط المطلوبة.
4. استخلاص الحل: بمجرد العثور على الصف الذي يحقق شروط المشكلة، يكون ذلك هو الحل.
متى نستخدمها؟
· عندما تتضمن المشكلة بيانات متعددة أو تحتاج لتتبع تغيرات القيم.· عندما نريد اكتشاف نمط معين.
· للمساعدة في حل المشكلات التي تحتوي على أكثر من متغير.
· عندما نريد تنظيم العمل لتجنب التكرار والفوضى.
مثال توضيحي (نفس المشكلة السابقة):
"متى يصبح عمر الأب ضعف عمر ابنه إذا كان عمر الأب الآن 40 سنة وعمر ابنه 10 سنوات؟"
المحاولة المدة الأب 40 الابن10 التحقق
1 5 45 15 لا 2 10 50 20 لا 3 15 55 35 لا 4 20 60 30 نعم
من الجدول، نرى بوضوح أن الحل هو بعد 20 سنة.
المميزات: منظمة، تقلل من الأخطاء، تظهر الأنماط بوضوح.العيوب: قد تستغرق وقتًا في التحضير، خاصة إذا كان نطاق الحلول المحتملة واسعًا.
استراتيجية بناء جدول (Make a Table)
المفهوم:
تنظيم البيانات في جدول لتسهيل عملية البحث عن الأنماط والعلاقات بين المتغيرات.
خطوات التطبيق:
1. تحديد المتغيرات في المسألة2. تصميم جدول يتضمن جميع الاحتمالات
3. ملء الجدول بشكل منهجي
4. تحليل البيانات للوصول إلى الحل
الفرق بين استراتيجية التخمين والتحقق واستراتيجية بناء جدول
التخمين والتحقق بناء جدول تعتمد على التقدير والتعديل تعتمد على التنظيم المنهجي تستغرق وقتاً أطول كثر تنظيماً وشمولاً تخمينات عشوائية نسبيا تغطي جميع الاحتمالات مناسبة للمسائل البسيطة مناسبة للمسائل المعقدة
نشاط
المسألة: مجموع عمرين ٤٠ سنة، والعمر الأكبر يزيد عن الأصغر بمقدار ٨ سنوات.فما هما العمران؟
الحل باستراتيجية التخمين والتحقق
الحل:
التخمين الأول: ٢٠ و٢٠ (المجموع ٤٠ لكن الفرق ٠)التحقق: الفرق ٠ ≠ ٨ (غير صحيح)
التخمين الثاني: ٢٢ و١٨ (المجموع ٤٠، الفرق ٤)
التحقق: الفرق ٤ ≠ ٨ (غير صحيح)
التخمين الثالث: ٢٤ و١٦ (المجموع ٤٠، الفرق ٨)
التحقق: الفرق ٨ = ٨ (صحيح)
الإجابة: العمران هما ٢٤ و١٦ سنة
الحل باستراتيجية بناء جدول(المجموع ٤٠ والفرق ٨)
محاولة الأول الثاني لمجموع الفرق التحقق 1 ٢٠ ٢٠ ٤٠ ٠ لا 2 ٢١ ١٩ ٤٠ ٢ لا 3 ٢٢ ١٨ ٤٠ ٤ لا 4 ٢٣ ١٧ ٤٠ ٦ لا 5 ٢٤ ١٦ ٤٠ ٨ نعم 6 ٢٥ ١٥ ٤٠ ١٠ لا
التحليل: من الجدول نلاحظ أن الصف الذي يحقق الشرطين (المجموع ٤٠ والفرق ٨) هو عندما يكون العمر الأول ٢٤ والثاني ١٦.
الإجابة: العمران هما ٢٤ و١٦ سنة
ملاحظات هامة
· استراتيجية التخمين والتحقق مفيدة عندما يكون نطاق الإجابات محدوداً
· استراتيجية الجدول تضمن عدم تفويت أي احتمال
· يمكن الجمع بين الاستراتيجيتين في المسائل المعقدة
· اختيار الاستراتيجية المناسب يعتمد على طبيعة المسألة
———————
مقارنة مفصلة بين الاستراتيجيتين
الجانب استراتيجيةالتخمين والتحقق استراتيجية بناء الجدول الفلسفة تعتمد على التجريب والخطأ تعتمد على الاستقصاء المنظم الأساس المنطقي تقدير ثم اختبار ثم تعديل تنظيم ثم تحليل ثم استنتاج نمط التفكير تفكير تكيفي مرن منهجي منظم التطبيق العملي الجانب التخمين والتحقق بناء الجدول الخطوات غير خطية متسلسلة الوقت متغير حسب دقة التخمينات يمكن تقديره مسبقاً الجهد مركز في التحليل والتعديل موزع على التنظيم والملء المخرجات والتعلم الجانب التخمين والتحقق بناء الجدول المهارات المطورة الحدس، المرونة، التكيف التنظيم، الدقة، التحليل الفائدة التعليمي فهم عمق المسألة فهم شمولية المسألة التوثيق صعب التوثيق الكامل سهل التوثيق والمراجعة
مثال تطبيقي مفصل
"اشترى أحمد عدداً من الكتب والأقلام. سعر الكتاب ١٥ ريالاً، وسعر القلم ٣ ريالات. إذا كان مجموع ما دفعه ٧٢ ريالاً، وعدد الأقلام يزيد عن عدد الكتببمقدار 6، فكم كتاباً وقلماً اشترى أحمد؟"
استراتيجية التخمين والتحقق (Guess & Check)
نذكّر المعطيات: سعر الكتاب 15، القلم 3، الفرق d=6، وعليه إذا كان عدد الكتب ك فالعددين هما ك و ك+6
لاحظ أن الحدّ الأقصى لعدد الكتب لا يمكن أن يزيد عن72/15 = 4
لأن 5 كتب تكلف 75 > 72.
إذن نجرب ك=0,1,2,3,4.
سعر الكتاب 15، سعرالقلم 3
الفرق بين عدد الكتب وعدد الأقلام 6
تخمين 0 كتاب وعدد الاأقلام = 6 المجموع 18
خمين 1 كتاب وعدد الأقلام = 7 المجموع = 15+21=36
تخمين 2 كتاب وعددالا أقلام = 8 المجموع =30+24=54
تخمين 3 كتب وعددالاأقلام = 9 المجموع= 45+27= 72
(لا حاجة لتجربة 4 لأن 3 أعطت الحل بالفعل.)
النتيجة (بالتخمين والتحقق): عددالكتب = 3، عددالأقلام = 9.
طريقة الحل باستخدام جدول
سعر الكتاب 15، سعرالقلم 3
نعرّف أعمدة الجدول: عدد الكتب ك، عدد الأقلام ق = ك+6، والمجموع 15ك + 3ق.
عددالكتب ك عددالكتب ك لمجموع = 15ك + 3ق مطابق 0 6 18 لا 1 7 36 لا 2 8 54 لا 3 9 72 نعم
من الجدول نرى مباشرة أن الصف الذي يعطي المجموع 72 هو: ك = 3، ق = 9.
مقارنة بين الاستراتيجيتن
الجانب استراتيجية بناء الجدول استراتيجيةالتخمين والتحقق المسألة معقدة ومتعددة المتغيرات بسيطة وواضحة نطاق الحلول ضمان شمولية الحل محدود الهدف تريد تحليل الأنماط والعلاقات تطوير الحدس الرياضي الوقت تحتاج توثيقاً كاملاً للحل ليس عاملاً حاسماً
الخلاصة والتوصيات
· ابدأ دائماً بفهم عميق للمسألة· اختر الاستراتيجية المناسبة لطبيعة المسألة
· لا تتردد في تغيير الاستراتيجية إذا لم تنجح
· وثق عملية الحل دائماً للتعلم منها
هذا الشرخ المفصل يوضح أن كل استراتيجية لها مزاياها وتطبيقاتها المناسبة، والطالب الحكيك هو من يتقن كليهما ويستخدم كل منها في موضعها الصحيح.
خلاصة
· التخمين والتحقق يشبه البحث عن شيء في غرفة مظلمة عن طريق التحرك بخطوات صغيرة والاصطدام بالجدران لتحديد موقعك.
· بناء الجدول يشبه إضاءة مصباح في تلك الغرفة ووضع خريطة على الطاولة لتحديد موقعك بدقة.
في كثير من الأحيان، يمكن الجمع بين الاستراتيجيتين: حيث يمكنك استخدام جدول لتنظيم عملية التخمين والتحقق، مما يمنحك قوة وكفاءة وسرعة الوصول للحل.
استراتيجية اكتشاف النمط (Look for a
Pattern) في حل المشكلات الرياضية
مفهوم الاستراتيجية:
هي استراتيجية تعتمد على ملاحظة تكرار أو تسلسل معيّن في الأعداد أو الأشكال أو العمليات الحسابية، واستخدام هذا التكرار أو العلاقة للتنبؤ بالنتيجة التالية
أو اكتشاف الحل العام للمشكلة. بمعنى آخر، الطالب يبحث عن نظام أو قاعدة متكررة في المسألة، ويستفيد منها لإيجاد الحل بسهولة بدل الحساب اليدوي لكل
خطوة.
خطوات تطبيق الاستراتيجية:
قراءة المسألة وفهمها بوضوح.يجب تحديد المطلوب، و القيم أو الأشكال أو العمليات المتكررة.
تمثيل المسألة بعدة حالات بسيطة.
مثل: إدخال القيم 1، 2، 3… لمعرفة كيف يتغير الناتج في كل مرة.
ملاحظة النمط أو القاعدة المتكررة.
تحديد العلاقة بين المدخلات والمخرجات (زيادة، مضاعفة، طرح ثابت، مثلثات، مربعات…).تعميم النمط. كتابة القاعدة العامة التي تم اكتشافها (مثلاً: الناتج = 2 × العدد + 1).
استخدام القاعدة لحل المسألة المطلوبة. تطبق القاعدة على القيم الأكبر أو النهائية للوصول إلى الحل بسرعة.
أمثلة على أنواع الأنماط:
نمط عددي: 2، 4، 8، 16، 32…
(يتضاعف كل مرة ×2)
نمط هندسي: عدد المربعات في كل صف يزداد بمقدار 2.
نمط شكلي: مثلث → مربع → خماسي → سداسي… (كل مرة نزيد ضلعًا واحدًا).
متى نستخدمها؟
عندما تظهر في المسألة علاقات متكررة أو سلاسل عددية.
في المتتاليات الحسابية والهندسية.
في المسائل اللفظية التي تتكرر فيها نفس الخطوات الحسابية أكثر من مرة.
عند دراسة أنماط النمو (مثل زيادة الطوب في بناء أو عدد المقاعد في صفوف المسرح).
مميزات الاستراتيجية:
تنمّي الاستنتاج المنطقي والقدرة على الملاحظة الدقيقة.
تجعل الحل أكثر كفاءة وسرعة.
تساعد على اكتشاف القوانين الرياضية بطريقة استقرائية.
تربط بين الرياضيات المجردة والأنماط الواقعية.
عيوبها:
أحيانًا يكون النمط غير واضح من البداية.
قد يكتشف الطالب نمطًا خاطئًا إذا لم يتحقق منه بدقة.
تحتاج إلى تركيز وملاحظة قوية.
دور المعلم:
تقديم أمثلة تحتوي على تسلسل واضح يمكن ملاحظته.
تشجيع الطلاب على وصف النمط بالكلمات قبل كتابته كقاعدة.
سؤال الطلاب دائمًا: “ما الذي تلاحظه؟ ما الذي يتكرر؟ كيف يتغير النمط في كل خطوة؟”
استراتيجية اكتشاف نمط
ما هي، كيف تطبَّق، وكيف تختلف عن بناء استراتيجية جدول
اولاً: ما هي استراتيجية «اكتشاف النمط»؟
هي طريقة منهجية لفهم تسلسل أو مجموعة من المواقف عن طريق ملاحظة التكرار والانتظام (الخصائص المتكررة)، ثم صياغة قاعدة عامة تفسِّر هذا النمطوتُتيح التوقع للخطوة التالية أو العموم.
بمعنى آخر: ننتقل من أمثلة فردية إلى وصف قاعدة ثم اختبارها وتعميمها /إثباتها.
ثانياً :خطوات تطبيقها (خُطوة بخُطوة)
1. الملاحظة :ـ انظر بعناية للعناصر المعطاة (أرقام، أشكال، علاقات). اكتب ما تلاحظه أولاً — لا تسرع للصياغة.
2. التوصيف اللفظي
ـ حاول وصف ما يحدث بكلمات بسيطة: «يزيد بــ3 ثم بــ5…»، «يتبدّل الاتجاه كل مرتين»، «الجبر يظهر مجموع ثابت»…
3. البحث عن دلائل رياضية
ـ احسب فروقًا متتالية، نسبًا، عوامل، تناظر.
4. اقتراح قاعدة (فرضية)
ـ صِغ قاعدة رياضية أو تعبيرًا (مثل: a_n = n^2+1 أو «أضيف 2 ثم أضيف 4 ثم 6 …»).
5. اختبار القاعدة على أمثلة جديدة
ـ طبق القاعدة على الحالات المعطاة وحالة إضافية متوقعة. إذا فشلت، عدّل القاعدة.
6. تعميم و/أو إثبات
ـ حاول كتابة الصيغة العامة (إن أمكن) وبيان سبب صحتها (برهان بسيط أو مبرهنة أو ملاحظات بنيوية).
7. استخدام القاعدة للتنبؤ أو البناء
ـ استعملها للتنبؤ بالعناصر التالية أو لحل مشكلة أوسع.
ثالثاً : أمثلة سريعة (لتوضيح التطبيق)
مثال 1 — متتالية عددية
المتتالية: 2,,5,\,10,\,17,\,…
• ملاحظات: فروق متتالية = 3,\,5,\,7,\,… — هذه فروق فردية متزايدة بــ2.
• استنتاج: الفروق تساوي 2n+1، مما يشير إلى أن a_n = n^2 + 1 (نختبر: n=1→2، n=2→5، صحيح).
• إذًا القاعدة: a_n = n^2 + 1.
مثال 2 — علاقة بين عددين (ارتباط مع سؤالك السابق)
• عددان مجموعهما = 25 (ثابت). حاصل الضرب = (مثلاً 144).
• اكتشاف النمط: نبحث عن أزواج a,b بحيث a+b=25 وab=144 نُحلّ معادلة t(25-t)=144 حيث t=a.
• هذا نهجٌ يعتمد الملاحظة والتحويل إلى معادلة قابلة للحل — مثال على اكتشاف علاقة مختبئة عبر المجموع/الضرب.
رابعاً : ما الفرق بين اكتشاف نمط وبناء جدول؟
أ. مفهومياً
• اكتشاف نمط = عملية فكرية/استدلالية للبحث عن القاعدة أو القاعدة العامة من بيانات أو أمثلة. يركِّز على التفسير والعموم والبرهان.
• بناء جدول = تقنية تنظيمية بحتة. نضع مدخلات/مخرجات (أو خطوة، فرق، ن)، ونستخدم الجدول لرؤية علاقات واضحة(مثل تزايد ثابت، ميل ثابت، نمط بصري).
ب. وظيفياً / متى نستخدم كلٍّ منهما؟• بناء جدول مفيد عندما تريد:
• تنظيم بيانات كثيرة،
• رؤية فروق/نسب بسرعة،
• اختبار فرضية على عدة حالات بسرعة.
• اكتشاف نمط مفيد عندما تريد:
• صياغة قاعدة عامة أو تعميم،
• إثبات سبب حدوث النمط،
• الربط بين البنية العددية/الهندسية ونظرية أوسع.
ج. العلاقة بينهما
• الجدول أداة مساعدة داخل استراتيجية اكتشاف النمط. غالبًا تبدأ بالملاحظة ثم تبني جدولًا لترتيب النتائج (قيمة n، قيمة العنصر، الفرق، النسبة) لتوضيح النمط.لكن وجود جدول لا يعني أنك وصلت للقاعدة النهائية بل هو خطوة عملية داخل عملية الاكتشاف.
د. مثال توضيحي مقابل
• نعطي المتتالية 2,5,10,17
• بناء جدول: تظهرفيه الفروق الفرق الأول الفرق الثاني ثابت=2.
• اكتشاف نمط: من الجدول نستنتج أن a_n = n^2 + 1 ونُبرهن ذلك عبر الاستقراء أو تحويل فروق إلى صيغة.
خامساً :نصائح عملية لتعلُّم/تعليم استراتيجية اكتشاف النمط
• ابدأ دائمًا بالملاحظة البسيطة والكتابة: ما الذي تراه؟• جرِّب أكثر من تمثيل: جدول، رسم نقطي، رسم أشكال، وصف لفظي.
• جرِّب عمليات بسيطة: فرق، نسبة، مربع/مكعب، مضروب، إزاحة، انعكاس.
• استخدم القواعد العكسية: حاول أن تفكِّك ما قد يجعل النمط يحدث (أين ظهر العامل الثابت؟).
• علِّم الطلاب/المتعلمين أن الفشل في صياغة قاعدة أولية طبيعي — التعديل والتجريب جزء من الاستراتيجية.
• اطلب إثباتًا؛ لا تكتفِ بالتخمين. الاستنتاج يحتاج اختبارًا على حالات إضافية أو برهانًا.
سادساً : نشاطات قصيرة لتطبيق ما تعلّمته
1. أعطِ المتتالية 3,6,11,18,27, اطلب بناء جدول احسب الفرق الأول والفرق الثاني ثم اكتشف القاعدة العامة.2. أعطِ أزواج أعداد حاصل جمعها ثابت (مثلاً 20) واطلب إيجاد كل الأزواج الممكنة ذات حاصل ضرب معين — استخدم الجدول ثم استنتج قاعدة عامة.
3. اطلب رسم نمط هندسي (مثل مربعات تُضاف بزاوية معينة) ولاحظ كيف ينمو المجموع/المحيط — من الرسم جدول → قاعدة.
سابعاً : خلاصة قصيرة:
• اكتشاف النمط = استراتيجية ذهنية تهدف لصياغة قاعدة وتعميمها و/أو إثباتها.• بناء جدول = أداة عملية لتنظيم البيانات تساعد في رؤية النمط لكنه ليس بديلاً عن التفكير والبرهان.
• الأفضل عمليًا: استخدم الجدول في خدمة اكتشاف النمط — الجمع بينهما أسرع وأقوى.
تطبيق استراتيجية اكتشاف النمط خطوة بخطوة على مثال ونرى كيف يمكن أن نستخدم الجدول كأداة داخلها.
نشاط
المتتالية التالية:
2, 5, 10, 17, 26
نريد اكتشاف النمط وتحديد القانون العام الذي يصفها.
الخطوة 1: الملاحظة
الأعداد تزداد، لكن ليس بزيادة ثابتة.لنجد الفروق بين كل حدٍّ والذي بعده.
الخطوة 2: بناء جدول بسيط (للمساعدة في الملاحظة)
رقم الحد (n) قيمة الحد (aₙ) الفروق بين الحدود الفروق الثانية
الفرق2 الفرق 1 القيمة الحد 2 3 2 1 5 5 2 2 10 3 7 17 4 2 9 26 5 6
نلاحظ أن الفروق الأولى: 3, 5, 7, 9أما الفروق الثانية فهي ثابتة (2)
الخطوة 3:ملاحظة النمط
ثبات الفروق الثانية يعني أن المتتالية تتبع نمطًا تربيعيًا (أي أن a_n دالة تربيعية في n).
نفترض أن:a_n = an^2 + bn + c
الخطوة 4:إيجاد القاعدة (بالتعويض)
نستعمل القيم الأولى لنعرف a, b, c:
n aₙ
1 2
2 5
3 10
نعوض في القانون:
1 عندما n=1: a + b + c = 2
2 عندما n=2: 4a + 2b + c = 5
3 عندما n=3: 9a + 3b + c = 10
نحلّ هذا النظام البسيط:
من (2)–(1): 3a + b = 3
من (3)–(2): 5a + b = 5
نطرح بينهما:
(5a + b) - (3a + b) = 5 - 3 \Rightarrow 2a = 2 \Rightarrow a = 1
نعوض في 3a + b = 3:
3(1) + b = 3 \Rightarrow b = 0
وأخيرًا في a + b + c = 2:
1 + 0 + c = 2 \Rightarrow c = 1
إذن:
a_n = n^2 + 1
الخطوة 5: التحقق
n=4 \Rightarrow 4^2 + 1 = 17
n=5 \Rightarrow 5^2 + 1 = 26
صحيح
الخطوة 6:التعميم والشرح اللفظي
القاعدة العامة:
كل حد في المتتالية يساوي مربع رقم الحد + 1
أي:
a_n = n^2 + 1
الخلاصة:• استخدمنا الجدول فقط كوسيلة تنظيمية لنرى الفروق.
• لكن الاستراتيجية الرئيسة كانت اكتشاف النمط من خلال الملاحظة ثم فرض علاقة ثم اختبارثم تعميم.
=============================================
مقارنة بين استراتيجية كتابة معادلة و استراتيجية كتابة قاعدة أو قانون
أولًا: استراتيجية كتابة معادلة (Write an Equation)
متى نستخدمها:
نستخدمها عندما يكون المطلوب إيجاد قيمة مجهولة واحدة أو أكثر، ويكون في المسألة علاقة عددية محددة بين كميات يمكن ترجمتها إلى معادلة جبرية.
بمعنى آخر:
إذا كانت المسألة تحتوي على:
كلمات مثل: أوجد، كم ثمن، كم عدد، كم طول، كم عمر…
ومعلومة أو أكثر تربط الكميات بعلاقة (جمع، طرح، ضرب، قسمة).
فإننا نستخدم استراتيجية كتابة معادلة.
ما يميزها:
تركز على العلاقات الجبرية المباشرة.
الهدف منها هو الحل العددي النهائي (قيمة المجهول).
المعادلة تمثل موقفًا واحدًا فقط.
أمثلة توضيحية:
مسألة عمرية:
“عمر خالد يزيد عن عمر أحمد بـ 5 سنوات، ومجموع عمريهما 25 سنة، كم عمر كل منهما؟”
نستخدم المعادلة:
س + (س + 5) = 25مسألة بيع وشراء:
“اشترى سالم 3 دفاتر و4 أقلام بمبلغ 42 ريالًا، وسعر القلم 3 ريالات، فما سعر الدفتر؟”
نكتب معادلة:
3س + 4×3 = 42
إذن: نستخدمها عندما نريد أن نعرف قيمة مجهول في موقف عددي محدد.
ثانيًا: استراتيجية كتابة قاعدة أو قانون (Write a Rule or Formula)
متى نستخدمها:
نستخدمها عندما يظهر في المسألة نمط متكرر أو علاقة عامة بين متغيرين، ونريد اكتشاف قاعدة يمكن تعميمها لتطبق على أي حالة مشابهة.
بمعنى آخر:
إذا كانت المسألة تتضمن:
مواقف تتكرر أو تتوسع (عدد الطاولات، عدد الصفوف، المربعات، الأيام…).
علاقة منتظمة بين عددين أو أكثر.
ونريد توقع أو تعميم النتيجة لأي عدد.
فإننا نستخدم استراتيجية كتابة قاعدة أو قانون.
ما يميزها:
تركز على العلاقات النمطية (patterns).
الهدف منها تعميم العلاقة وليس مجرد إيجاد عدد واحد.
تنتج صيغة أو قاعدة يمكن تطبيقها لاحقًا.
أمثلة توضيحية:
الطاولات والكراسي (نمط متكرر):
طاولة واحدة = 4 كراسي
طاولتان متجاورتان = 6 كراسي
3 طاولات = 8 كراسي
نلاحظ النمط، فنستنتج قاعدة:
ك = 2ن + 2المستطيلات:
إذا كان طول المستطيل = 3 × عرضه دائمًا،
فنكتب القاعدة:
ل = 3عإذن: نستخدمها عندما نبحث عن العلاقة العامة بين المتغيرات وليس مجرد قيمة واحدة.
مقارنة ختامية لتوضيح متى نستخدم كل استراتيجية:
المقارنة
كتابة معادلة
كتابة قاعدة أو قانون
الهدف
إيجاد قيمة مجهول معين في حالة واحدة
إيجاد علاقة عامة بين كميات
متى نستخدمها
عند وجود علاقة عددية محددة ومعطيات كافية لحساب مجهول
عند وجود نمط متكرر أو علاقة يمكن تعميمها
التركيز
على حل معادلة عددية
على بناء علاقة أو قانون
الناتج
قيمة عددية محددة
قاعدة عامة (صيغة أو دالة)
المثال
“كم ثمن القلم؟”
“كم عدد الكراسي لأي عدد من الطاولات؟”
الأداة الرياضية
المعادلة الجبرية
الدالة أو العلاقة الرياضية
الفرق بين استراتيجية كتابة معادلة و استراتيجية كتابة قاعدة أو قانون دقيق، لكنه مهم جدًا في تدريس حل المشكلات الرياضية.
أولاً: استراتيجية كتابة معادلة
الفكرة:
تحويل المشكلة اللفظية إلى معادلة رياضية تحتوي على متغير (س) يمكن حلها لإيجاد المجهول.
الهدف:
تمثيل الموقف الرياضي بعدد أو متغير مجهول، ثم إجراء عمليات جبرية للوصول إلى الحل.
الخطوات:
فهم المعطيات والمطلوب.
تمثيل الكمية المجهولة برمز (مثل س).
التعبير عن العلاقة بين الكميات بمعادلة.
حل المعادلة لإيجاد قيمة المتغير.
مثال:
اشترى أحمد 3 دفاتر وثلاثة أقلام بـ 42 ريالًا.إذا كان سعر الدفتر 10 ريالات، فما سعر القلم؟
الحل بطريقة كتابة معادلة:
نرمز لسعر القلم بـ (س).
إذن:
3×10 + 3×س = 42
30 + 3س = 42
3س = 12
س = 4
سعر القلم = 4 ريالات.
هنا الاستراتيجية حولت النص إلى معادلة رياضية فيها مجهول واحد.
ثانيًا: استراتيجية كتابة قاعدة أو قانون
الفكرة:
تستخدم عندما تتكرر المشكلة أو تتبع نمطًا رياضيًا ثابتًا، فنبحث عن علاقة عامة (قاعدة) تربط بين المتغيرات.
الهدف:
اكتشاف قاعدة عامة أو علاقة رياضية يمكن تطبيقها مباشرة على مسائل مشابهة.
الخطوات:
دراسة العلاقة بين القيم في المسألة.
تحديد النمط أو العلاقة.
صياغة قاعدة عامة (قانون).
تطبيق القاعدة على الحالة المطلوبة.
مثال:
في صف من الطاولات المربعة المتجاورة، كل طاولة لها 4 كراسي، وعند وضع طاولتين متجاورتين يُزال كرسيان متقابلان.
اكتب قاعدة لحساب عدد الكراسي (ك) عند وجود (ن) طاولات.
الحل بطريقة كتابة قاعدة أو قانون:لكل طاولة 4 كراسي، لكن كل طاولة إضافية تزيل كرسيين مشتركين.
إذن القاعدة هي:
ك = 4ن - 2(ن - 1)
أو بعد التبسيط:
ك = 2ن + 2
هنا تم اكتشاف علاقة عامة (قاعدة) تربط بين عدد الطاولات وعدد الكراسي — يمكن تطبيقها على أي عدد ن.
الفرق في جوهره:
المقارنة
كتابة معادلة
كتابة قاعدة / قانون
الهدف
إيجاد قيمة مجهول محدد
إيجاد علاقة عامة أو قانون متكرر
الاستخدام
في مسألة واحدة محددة
في مسائل تتبع نمطًا متكررًا
النتيجة
عدد (حل واحد)
تعبير عام أو صيغة
الأداة الرئيسة
معادلة تحتوي على متغير واحد أو أكثر
علاقة تربط بين متغيرين أو أكثر
مثال نموذجي
“كم ثمن القلم؟”
“كم عدد الكراسي لأي عدد من الطاولات؟”
التمييز بين
استراتيجية كتابة معادلة
استراتيجية كتابة قاعدة (أو قانون)
استراتيجية البحث عن نمط
الاستراتيجيات الثلاث تبدو متشابهة ظاهريًا، لكنها تختلف في طريقة التفكير والهدف من استخدامها.
أولًا: استراتيجية كتابة معادلة
الفكرة:
تحويل المسألة اللفظية إلى معادلة جبرية تحتوي على مجهول (س)، وحلها للحصول على قيمة محددة.
نستخدمها عندما:
يكون في المسألة علاقات حسابية واضحة بين كميات.
نحتاج لإيجاد قيمة مجهولة واحدة.
التركيز:
الترجمة إلى رموز ومعادلات لحلها.
مثال:
اشترى أحمد 3 دفاتر وسعر الدفتر 8 ريالات، ودفتر آخر أغلى بـ 4 ريالات. كم المبلغ الذي دفعه؟
نرمز لسعر الدفتر الغالي بـ (س):8×3 + س = 28
ثم نحسب المجهول.
هدفها: الوصول إلى قيمة عددية لمجهول.
ثانيًا: استراتيجية كتابة قاعدة أو قانون
الفكرة:
تُستخدم عندما يكون هناك نمط ثابت أو علاقة متكررة يمكن التعبير عنها بقانون عام يربط بين متغيرين أو أكثر.
نكتشف العلاقة ثم نصوغها كـ قاعدة عامة أو صيغة رياضية.
نستخدمها عندما:
تظهر علاقة منتظمة بين القيم.
نريد صياغة علاقة عامة تُستخدم لأي حالة مشابهة.
التركيز:
تعميم العلاقة في شكل قاعدة أو معادلة عامة.
مثال:
عدد الكراسي حول ن طاولات مربعة متجاورة:
1 طاولة → 4 كراسي
2 طاولات → 6 كراسي
3 طاولات → 8 كراسي
إذن القاعدة:
ك = 2ن + 2
هدفها: بناء علاقة عامة تصلح لأي عدد من الطاولات.
ثالثًا: استراتيجية البحث عن نمط (Look for a Pattern)
الفكرة:
هي المرحلة السابقة لكتابة القاعدة — أي أننا نبحث في الأعداد أو الأشكال عن تسلسل أو انتظام يساعدنا على التنبؤ أو اكتشاف العلاقة.
نستخدمها عندما:
لا نعرف القاعدة بعد.
نلاحظ تكرارًا أو تسلسلًا في القيم.
نريد أن نستنتج النمط الذي يقودنا لاحقًا إلى القاعدة أو القانون.
التركيز:
اكتشاف النمط من خلال الملاحظة (وليس الحساب الجبري).
مثال:
عدد النقاط في كل شكل من سلسلة مثلثات:
الشكل 1 = 3 نقاط
الشكل 2 = 6 نقاط
الشكل 3 = 9 نقاط
نلاحظ النمط (كل مرة +3)،
إذن النمط: “نضرب رقم الشكل × 3”
ثم نكتب القاعدة:
ع = 3ن
هدفها: إيجاد العلاقة المتكررة أو التسلسل الذي يقود إلى قاعدة.
مقارنة شاملة بين الاستراتيجيات الثلاث:
المقارنة
كتابة معادلة
كتابة قاعدة أو قانون
البحث عن نمط
الهدف
إيجاد قيمة مجهول محدد
إيجاد علاقة عامة تربط المتغيرات
اكتشاف العلاقة أو النمط من خلال الملاحظة
المدخل
ترجمة المعطيات إلى معادلة جبرية
بناء قاعدة بعد معرفة العلاقة
الملاحظة ثم اكتشاف النمط التدريجي
التركيز
الحساب والتحليل الجبري
التعميم الرياضي
الملاحظة والتكرار
المخرج النهائي
عدد (قيمة محددة)
قاعدة أو قانون
وصف للنمط أو قاعدة أولية
الأداة الرئيسة
المعادلة الجبرية
الصيغة أو القاعدة العامة
الجداول أو الرسومات أو التسلسل العددي
مثال نموذجي
“كم ثمن القلم؟”
“كم عدد الكراسي لأي عدد من الطاولات؟”
“كيف يزداد عدد النقاط في كل شكل؟”
العلاقة بينهما
ناتجها رقم واحد
ناتجها قاعدة عامة
تمهيد للوصول إلى القاعدة
للتوضيح أكثر:
يمكن أن نستخدم الاستراتيجيات الثلاث في مراحل متتابعة:
نلاحظ النمط أولًا (استراتيجية البحث عن نمط).
نكتب قاعدة عامة بناءً عليه (استراتيجية كتابة قاعدة).
نستخدم القاعدة في مسألة محددة ونكوّن معادلة لحلها (استراتيجية كتابة معادلة).
علاقة استراتيجية بناء جدول
ب
استراتيجية كتابة معادلة
استراتيجية كتابة قاعدة (أو قانون)
استراتيجية البحث عن نمط
استراتيجية بناء جدول في كثير من الأحيان تكون حلقة الوصل بين الاستراتيجيات الثلاث.
أولًا: تعريف استراتيجية بناء جدول (Make a Table)
الفكرة العامة:
هي تنظيم المعطيات والعلاقات في جدول مرتب لتسهيل الملاحظة والمقارنة واكتشاف العلاقات بين القيم.
الجدول يساعد الطالب على رؤية الأنماط والعلاقات بوضوح قبل أن ينتقل إلى مرحلة المعادلة أو القاعدة.
متى نستخدم استراتيجية بناء جدول؟
نستخدمها عندما:
تحتوي المسألة على قيم متعددة أو متغيرة.
يكون من الصعب ملاحظة العلاقة مباشرة من النص.
نريد تنظيم البيانات لتسهيل البحث عن نمط أو قاعدة.
نحتاج إلى التجربة المنظمة وتسجيل النتائج خطوة بخطوة.
أمثلة توضّح دورها:
المثال 1 – علاقة مع “البحث عن نمط”:
في الشكل الأول مثلث واحد، في الشكل الثاني مثلثان، في الثالث ثلاثة مثلثات…
كم عدد المثلثات في الشكل السادس؟
هنا نبني جدولًا:
رقم الشكل (ن)
عدد المثلثات
1
1
2
2
3
3
4
4
5
5
6
?
بعد الملاحظة نرى النمط واضحًا: العدد يزداد بمقدار 1 في كل مرة →
القاعدة: ع = ن
العلاقة: الجدول ساعدنا على اكتشاف النمط.
المثال 2 – علاقة مع “كتابة قاعدة أو قانون”:
طاولات مربعة متجاورة، كل طاولة لها 4 كراسي، والطاولة الثانية تشارك كرسيين مع الأولى.
اكمل الجدول ثم اكتب قاعدة لعدد الكراسي.
عدد الطاولات (ن)
عدد الكراسي (ك)
1
4
2
6
3
8
4
10
من الجدول نلاحظ النمط: كل مرة +2
إذن القاعدة: ك = 2ن + 2
العلاقة: الجدول جعل اكتشاف القاعدة سهلًا وواضحًا.
المثال 3 – علاقة مع “كتابة معادلة”:
مجموع عددين = 25، وأحدهما أكبر من الآخر بـ 7.
كم العددان؟
يمكن أن نبدأ بجدول محاولات منظمة:
العدد الأول
العدد الثاني
المجموع
8
15
23
9
16
25 ✅
ثم نترجم العلاقة إلى معادلة:
س + (س + 7) = 25
العلاقة: الجدول ساعد على التجريب المنظم قبل الانتقال إلى المعادلة الجبرية.
إذن ما علاقة “بناء جدول” بالاستراتيجيات الثلاث؟
الاستراتيجية
العلاقة مع “بناء جدول”
البحث عن نمط
الجدول يُستخدم لتنظيم القيم لملاحظة النمط بسهولة.
كتابة قاعدة أو قانون
بعد ملاحظة النمط من الجدول، نكتب القاعدة التي تعبّر عنه.
كتابة معادلة
الجدول قد يساعدنا على اكتشاف العلاقة الرقمية ثم ترجمتها إلى معادلة لحل مجهول.
الخلاصة:
استراتيجية بناء جدول ليست بديلاً عن الاستراتيجيات الأخرى،بل هي أداة مساعدة تُستخدم في المراحل الأولى من التفكير المنظم لتسهيل الوصول إلى:
- من النمط الى القاعدة ثم المعادلة.
يمكن تلخيصها بهذا الترتيب المنطقي:
1-بناء جدول
2- البحث عن نمط
3- كتابة قاعدة
4- كتابة معادلة
=========================================================================================
استراتيجية التجربة المنظمة (Systematic Trial)
هي طريقة لحل المشكلات تعتمد على تجربة عدد من الحلول الممكنة بطريقة منظمة ومنطقية حتى يتم الوصول إلى الحل الصحيح.
أي أن الطالب لا يجرّب عشوائيًا، بل ينظّم تجاربه وفق خطوات محددة أو تسلسل منطقي (مثل زيادة أو إنقاص عدد ثابت كل مرة، أو تغيير متغير واحد
فقط في كل محاولة).
هدفها:
• تدريب الطالب على تنظيم المحاولات.
• تقليل العشوائية في التجريب.
• الموازنة بين المنهجية والتفكير المنطقي.
خطوات استراتيجية التجربة المنظمة:
1. فهم المعطيات والمطلوب.
2. تحديد جميع الاحتمالات الممكنة.
3. تجريب كل احتمال بشكل منظم (من الأصغر إلى الأكبر مثلًا).
4. تسجيل النتائج وملاحظتها.
5. التحقق من تحقق الشروط للوصول إلى الحل الصحيح.
الفكرة:
تجريب القيم بطريقة مرتبة ومنهجية دون الحاجة إلى كتابة جدول كامل، أي باتباع نظام منطقي في المحاولات.
خطوات الحل:
نبدأ بتخمين عدد قريب من نصف 25 (أي 12 أو 13).
نحسب العدد الآخر:
إذا اخترنا الأول 12 و الثاني 13 فان حاصل الضرب = 156 (أكبر من 144).
نعلم أن حاصل الضرب كبير بمعنى أننا نحتاج فرقًا أكبر بين العددين.
نجرب الأول 9 و الثاني 16 ضربهما 9×16=144 .
الميزة:
منظمة لكنها لا تتطلب جدولًا مكتملًا.
تركز على المنطق الرياضي لتقريب النتيجة في كل خطوة.
تعزز التفكير الاستدلالي عند الطالب.
العيب:
تتطلب من الطالب فهم العلاقة بين المجموع والضرب.
مثال تطبيقي:
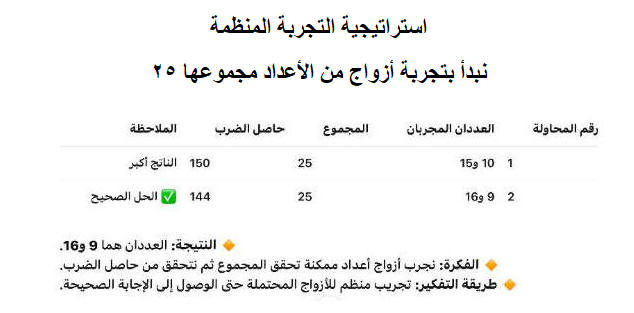
عددان مجموعهما 25، وحاصل ضربهما 144. أوجد العددين.
المحاولة
العدد الأول
العدد الثاني
المجموع
حاصل الضرب
الملاحظة
1
10
15
25
150
أكبر من المطلوب
2
9
16
25
144
✅ الحل الصحيح
النتيجة: العددان هما 9 و16.
مزايا الاستراتيجية:
• تجعل الطالب يفكر بشكل منظم ومنطقي.
• تمنع العشوائية في التجريب.
• تناسب المسائل العددية أو المشكلات التي تتضمن علاقات رياضية بسيطة.
متى نستخدمها؟
• عندما تحتوي المسألة على عدد محدود من الاحتمالات.
• وعندما لا يمكن الوصول للحل مباشرة باستخدام معادلات
الفرق بين استراتيجية بناء جدول واستراتيجية التجربة المنظمة
| الجانب |
بناء جدول |
التجربة المنظمة |
|
طريقة العرض |
جدول مرتب بكل المحاولات |
محاولات مرتبة ومنطقية بدون جدول كامل |
|
أسلوب العمل |
يعتمد على الترتيب البصري للأعداد |
يعتمد على التفكير التحليلي لتقليل المحاولات |
|
مناسب لمن؟ |
للطلاب الذين يفضلون التنظيم البصري |
للطلاب الذين يفضلون التحليل والاستنتاج |
|
عدد المحاولات |
أكثر عادة |
أقل وأكثر دقة |
|
سهولة التطبيق |
أسهل في البداية |
يحتاج تدريبًا بسيطًا |
|
الهدف التعليمي |
توضيح الأنماط العددية |
تطوير التفكير المنطقي |
الفرق بين استراتيجية بناء جدول واستراتيجية لتجربة المنظمة
يبدو أن كلتا الاستراتيجيتين تستخدمان الجداول، لكن هناك فرق في الهدف وطريقة التفكير. فيما يلي توضيح الفرق بينهما
| الجانب |
بناء جدول |
التجربة المنظمة |
|
الفكرة الأساسية |
تنظيم القيم في جدول لاكتشاف العلاقة الرياضية. |
تجربة حلول محتملة بطريقة مرتبة حتى الوصول للحل الصحيح. |
|
الهدف |
اكتشاف العلاقة بين المتغيرات أو القيم. |
إيجاد الحل الصحيح من بين عدة احتمالات. |
|
طريقة العمل |
نبني جدولًا يوضح العلاقة بين القيم ونستنتج القاعدة. |
نحدد جميع الاحتمالات الممكنة ونختبرها واحدة تلو الأخرى. |
|
نوع المسائل |
المسائل التي فيها علاقة بين كميات مثل السعر × العدد = المجموع. |
المسائل التي فيها أكثر من احتمال مثل المجموع والضرب. |
|
عدد المحاولات |
أقل لأن الجدول منظم وفق علاقة محددة. |
عادة أكثر لأننا نجرب احتمالات متعددة. |
|
دور الجدول |
لاكتشاف العلاقات الرياضية. |
لتنظيم التجارب فقط. |
مقارنة
|
بناء جدول |
التجربة المنظمة |
| تنظيم البيانات والعلاقاتلاكتشاف نمطأو قاعد رياضية | تنظيم المحاولاات المتتعددة للوصول الى الحل الصحيح |
| تفكير تحليلي (ملاحظة العلاقات بين القيم للوصول الى علاقة ثابتة | تفكير تجريبي احتمالات اسبعاد غير الصحيح حتى الوصول للمطلوب |
| قاعدة أو علاقة يمكن تعميمها أو تطبيقها على مسائل أخرى | حل محدد لمسألة فيها شروط معينة |
| المسائل التي تتطلب علاقة بين كميتين | المسائل التي فيها احتمال أكثر من اجابة |
في استراتيجية بناء جدول أنت تبني جدول لتوضيح العلاقة الرياضية أو النمط
في استراتيجية التجربة المنظمةأنت تبني جدول لتجريب حلول ممكمة
نشاط
عددان مجموعهما 25 وحاصل ضربهما 144
فما العددان؟
| الأول س | الثاني(ص= 25-س | حاصل الضرب | الملاحظة |
| 10 | 15 | 150 | اأكبر |
| 11 | 14 | 154 | أكبر |
| 12 | 13 | 156 | أكبر |
| 9 | 16 | 144 | يساوي |
مثال 1: استراتيجية التجربة المنظمة
المسألة: عددان مجموعهما 25 وحاصل ضربهما 144.
ننشئ جدولًا للأزواج الممكنة التي مجموعها 25 ونحسب حاصل ضربها حتى نجد الزوج الصحيح:
|
المحاولة |
العدد الأول |
العدد الثاني |
المجموع |
حاصل الضرب |
|
1 |
1 |
24 |
25 |
24 |
|
2 |
2 |
23 |
25 |
46 |
|
3 |
3 |
22 |
25 |
66 |
|
4 |
4 |
21 |
25 |
84 |
|
5 |
5 |
20 |
25 |
100 |
|
6 |
6 |
19 |
25 |
114 |
|
7 |
7 |
18 |
25 |
126 |
|
8 |
8 |
17 |
25 |
136 |
|
9 |
9 |
16 |
25 |
144 ✅ |
لاحظ أن المحاولة رقم واحد كان حاصل الضرب قليل جدا عن المطلوب كان من الافضل زياة الفرق بدل من المحاول رقم 2 وكان من الأفضل البدء
بتجربة العديد 10 و 15
كما هو واضح في الجدول التالي
النتيجة: العددان هما 9 و16.
الفرق بين استراتيجية التجربة المنظمة واستراتيجية بناء جدول من حيث الفكرة، وطريقة الحل، وسنستخدم مثالًا واحدًا
يُحل بالطريقتين مع جدول مقارنة واضح بينهما.
أولًا: الفرق في الفكرة العامة
وجه المقارنة
استراتيجية التجربة المنظمة
استراتيجية بناء جدول
الفكرة الأساسية
تجربة حلول متعددة بطريقة منظمة للوصول إلى الحل الصحيح.
تنظيم البيانات في جدول لاكتشاف العلاقة بين القيم.
طريقة الحل
نبدأ بتجربة قيم محتملة بشكل منظم ونفحص صحتها واحدة تلو الأخرى.
نرتب المعطيات في جدول لتوضيح النمط أو العلاقة الرياضية.
الهدف
إيجاد الحل الصحيح بعد عدد من المحاولات المنظمة.
فهم العلاقة بين المتغيرات للوصول إلى قاعدة عامة أو نتيجة مباشرة.
متى تستخدم
عند وجود احتمالات متعددة للحل ولا توجد صيغة مباشرة للحساب.
عندما تساعد العلاقات المنتظمة بين الأعداد على تبسيط الحل.
المناسب للطلاب
الطلاب في المراحل المتوسطة عند حل المسائل العددية والتجريبية.
الطلاب الذين يتعاملون مع أنماط عددية أو علاقات متكررة.
ثانيًا: المثال المشترك
المسألة:
مجموع عددين 25، وحاصل ضربهما 144.
أوجد العددين باستخدام:
- استراتيجية التجربة المنظمة
- استراتيجية بناء جدول
أولًا: الحل باستخدام استراتيجية التجربة المنظمة
نبحث عن عددين مجموعهما 25 وحاصل ضربهما 144، فنبدأ بتجربة أزواج الأعداد الممكنة بطريقة مرتبة:
العدد الأول
العدد الثاني
حاصل الضرب
النتيجة
10
15
150
أكبر من 144
11
14
154
أكبر من 144
12
13
156
أكبر من 144
9
16
144
مناسب
النتيجة: العددان هما 9 و16.
استخدمنا المحاولة المنظمة حتى وصلنا للحل الصحيح دون عشوائية.
ثانيًا: الحل باستخدام استراتيجية بناء جدول
ننشئ جدولًا لتوضيح العلاقة بين العدد الأول والثاني وحاصل ضربهما:
العدد الأول (x)
العدد الثاني (25 - x)
حاصل الضرب (x × (25 - x))
10
15
150
9
16
144 ****
8
17
136
النتيجة: العددان هما 9 و16.
هنا استخدمنا الجدول لترتيب البيانات وملاحظة العلاقة بين الأعداد وحاصل الضرب.
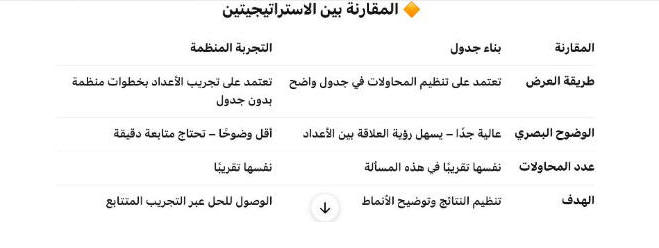
ثالثًا: المقارنة بين الحلّين
وجه المقارنة
استراتيجية التجربة المنظمة
استراتيجية بناء جدول
طريقة التفكير
التجريب المنظم خطوة بخطوة حتى نجد الحل.
عرض البيانات في جدول لتوضيح العلاقة بين القيم.
التركيز
على اختبار قيم محتملة واحدة تلو الأخرى.
على تحليل العلاقة بين المتغيرين من خلال الجدول.
سهولة الاكتشاف
مناسبة عندما يكون عدد المحاولات محدودًا.
مناسبة عندما تتكرر العلاقة بانتظام ويمكن ملاحظتها بصريًا.
الهدف من الاستراتيجية
الوصول إلى حل صحيح بعد تجارب مرتبة.
فهم العلاقة العددية للوصول إلى قاعدة أو نتيجة مباشرة.
مثال التطبيق
تجربة أعداد تحقق مجموعًا وضربًا معينًا.
تنظيم العلاقة (x , 25 - x) لمعرفة ناتج الضرب الصحيح.
عددان مجموعهما 25، وحاصل ضربهما 144. أوجد العددين.
استراتيجية بناء جدول
|
العدد الأول (س) |
العدد الثاني (ص = 25 - س) |
حاصل الضرب (س × ص) |
الملاحظة |
|
10 |
15 |
150 |
أكبر من المطلوب |
|
11 |
14 |
154 |
أكبر من المطلوب |
|
12 |
13 |
156 |
أكبر من المطلوب |
|
9 |
16 |
144 |
الحل الصحيح |
الفكرة:
نرتب القيم في جدول لنرى العلاقة بين العددين.
النتيجة: 9 و16
ملاحظات: بصري ومنظم جدًا، مناسب لتعليم الطلاب.
استراتيجية التجربة المنظمة
|
رقم المحاولة |
الأعداد |
المجموع |
حاصل الضرب |
الملاحظة |
|
1 |
10 و15 |
25 |
150 |
أكبر من المطلوب |
|
2 |
9 و16 |
25 |
144 |
الحل الصحيح |
الفكرة:
نجرب أزواج أعداد تحقق المجموع، ثم نتحقق من حاصل الضرب.
النتيجة: 9 و16
ملاحظات: أقل وضوحًا بصريًا، لكنها مرتبة ومنهجية.
استراتيجية التخمين والتحقق
|
المحاولة |
الأعداد |
المجموع |
حاصل الضرب |
الملاحظة |
|
1 |
10 و15 |
25 |
150 |
أكبر من المطلوب |
|
2 |
9 و16 |
25 |
144 |
الحل الصحيح |
الفكرة:
التخمين الأول يعطي فكرة عن اتجاه التعديل.
النتيجة: 9 و16
ملاحظات: سريع إذا التخمين موفق، يعتمد على الحدس والتحليل الذكي.
المقارنة بين الاستراتيجيات الثلاث
|
جانب المقارنة |
بناء جدول |
التجربة المنظمة |
التخمين والتحقق |
|
طريقة العمل |
تنظيم القيم في جدول كامل |
تجربة أزواج مرتبة |
تخمين وتعديل حسب النتيجة |
|
الوضوح البصري |
عالي جدًا |
متوسط |
منخفض |
|
السرعة |
متوسط |
متوسط |
سريع إذا التخمين موفق |
|
الهدف |
رؤية العلاقة بين العددين |
التحقق من صحة المحاولات |
الوصول للحل الصحيح بسرعة |
|
عدد المحاولات |
أكثر لكن منظم |
يعتمد على ترتيب المحاولات |
غالبًا أقل إذا التخمين موفق |
|
الملاءمة للمرحلة المتوسطة |
عالي ✅ |
جيد ✅ |
متوسط ⚠️ |
عددان مجموعهما 25، وحاصل ضربهما 144. أوجد العددين.
العددان س و (25- س)
س (25- س) = 144
25س - س2=144
س2 - 25س +144= 0
(س-9)(س-16)=0
س=9
س=16