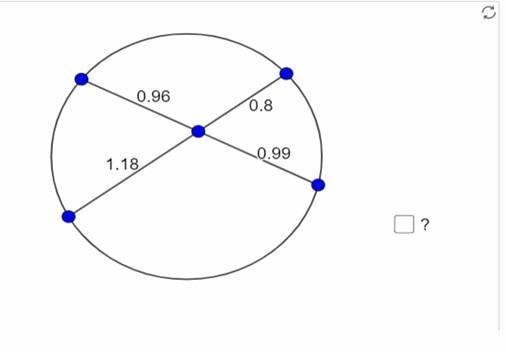
الوتران المتقاطعان في دائرة
Intersecting Chords
الهدف العام:
التوصل لخاصية الوترين المتقاطعين في دائرة
الأهداف التفصيلية:
- التعرف على مفهوم الوتر في دائرة
- التوصل لخاصية الوترين المتقاطعين في الدائرة من خلال ضرب جزئي الوتر الأول ومقارنته بحاصل ضرب جزئي الوتر الثاني.
تمهيد:
مفهوم الوتر في دائرة: هو القطعة المستقيمة الواصلة بين نقطتين على الدائرة. وعلى ذلك يسمى الوتر المار بنقطة مركز الدائرة قطراً في الدائرة.
شرح البرمجية والخطوات التفصيلية
بعد الضغط على رابط البرمجية ستنتقل إلى الصفحة التالية:
أولاً: شرح الرموز وآلية عمل البرمجية
· : الدائرة الزرقاء الواقعة داخل الدائرة هي نقطة تقاطع الوترين، والدوائر الزرقاء الواقعة على الدائرة بالضغط عليها والسحب ستجد أنها تعمل على تحريك الأوتار داخل الدائرة وبالتالي تغيير أطوال جزئي كل وتر كالتالي:
:
هذه الايقونة عند الضغط عليها ستحصل على ناتج ضرب جزئي كل وتر ومقارنته بحاصل ضرب
جزئي الوتر الآخر. (لا تضغط عليها الآن انتظر حتى نهاية
الدرس).
:
هذه الايقونة عند الضغط عليها ستعود للصفحة الرئيسية الأولى (اضغط
عليها الآن لنبدأ العمل).
ثانياً: شرح الفكرة القائمة عليها البرمجية وخطوات العمل
تقوم الفكرة على التوصل لخاصية الوترين المتقاطعين في الدائرة من خلال ضرب جزئي كل وتر في بعضهما ومقارنة الناتج بينهما كالتالي:
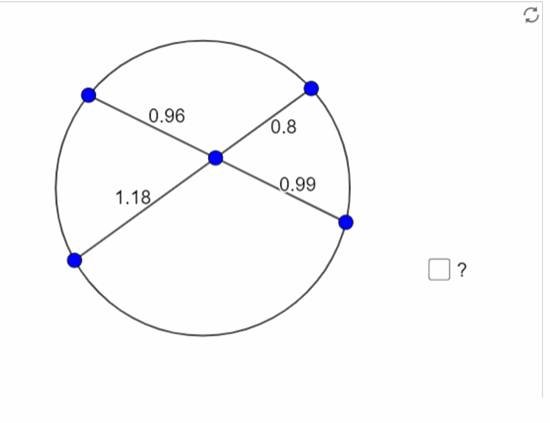
الخطوة الأولى:
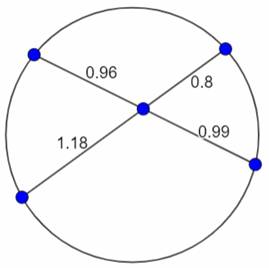
س/ احسب حاصل ضرب جزئي كل وتر على حده على النحو التالي:
0.8 × 1.18= ؟ 0.99 × 0.96 = ؟
أحسنت الآن تأكد من حاصل الضرب لكلا العمليتين بالضغط على المربع الذي بجانب عملية
الاستفهام 
كالتالي:
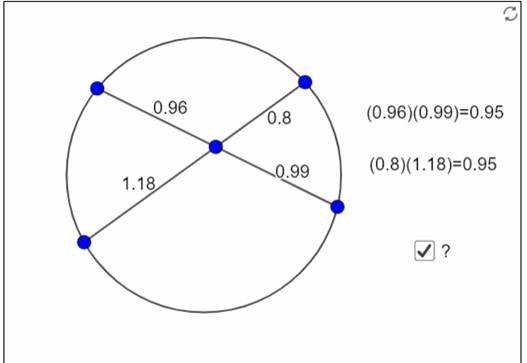
س/ ماذا تلاحظ على ناتج حاصل ضرب العمليتين (ضرب جزئي كل وتر ومقارنته بضرب جزئي الوتر الآخر)؟
الخطوة الثانية:
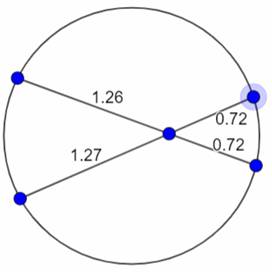
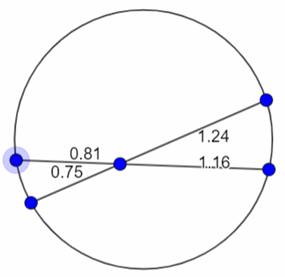
قم بتحريك الدوائر الزرقاء على الدائرة لتحريك الأوتار داخل الدائرة وتغيير أطوال جزئي كل وتر، وعلى سبيل المثال كالتالي:
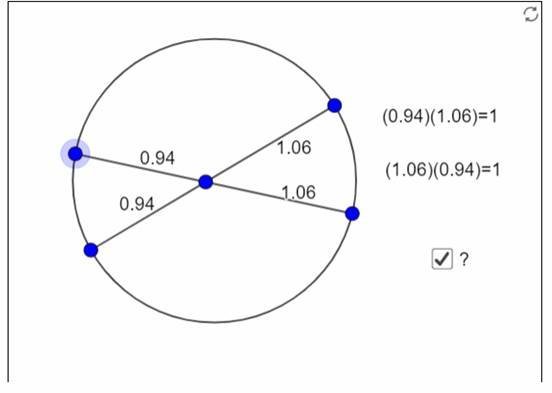
س/ ماذا تلاحظ على ناتج حاصل ضرب جزئي كل وتر ومقارنته بحاصل ضرب جزئي الوتر الآخر؟
أحسنت، لقد وجدت بأنه عند ضرب جزئي كل وتر ومقارنته بحاصل ضرب الجزئين الآخرين على الوتر الآخر فإن القيمة متساوية.
وبالتالي ستتوصل للنتيجة التالية:
إذا تقاطع وتران داخل الدائرة فإن حاصل ضرب طولي جزئي كل وتر متساويان
--------------------------------------------------------------