حل أنظمة المعادلات بيانياً
رابط البرمجية
https://www.geogebra.org/m/eqzktUFP
الهدف من البرمجية
حل أنظمة المعادلات في متغيرين
بيانياً
شرح أنظمة معادلات الدرجة
الأولى
المعنى الهندسي للنظام الخطي
يمثل النظام الخطي العام المتكون من معادلتين خطيتين بمتغيرينx و y
بالصيغة الآتية:
a1x +b1y = c1
A2x + b2y = c2
إن الشكل الهندسي لهذه المعادلات هو الخطوط المستقيمة L1 و L2 كما في الشكل (1-1) ولما
كانت النقطة (x
،
y) تقع على المستقيم إذا
وفقط إذا كانت x
و y تحقق معادلة المستقيم، فإن
حلول النظام الخطي تقابل المستقيمين L1
و L2 كما موضح في الشكل (1-1).
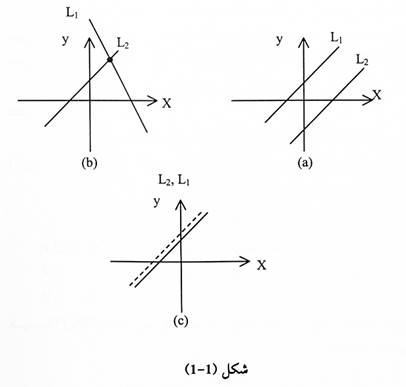
من خلال الشكل (1-1) يتضح أن هناك ثلاث احتمالات للحلول وهي:
1- المستقيمان L2 ، L1
متوازيان، أي لا يوجد نقطة تقاطع، وعليه فليس للنظام الخطي حل [شكل (1-1)a ].
2- المستقيمان L2 ، L1
يتقاطعان بنقطة، وهذا يعني أن النظام الخطي له حل واحد فقط [الشكل (1-1)b].
3- المستقيمان متطابقان، اي يوجد عدد غير محدود من الحلول [شكل
(1-1)c].
نستنتج من ذلك أن أي نظام خطي إما ليس له حل او له حل واحد فقط
أو له عدد غير منتهي من الحلول.
تسمى المجموعة المنتهية المتكونة من m من المعادلات الخطية، التي
تحوي على n
من المتغيرات xn،…،،
x2 ، x1 نظام المعادلات الخطية.
وتسمى أيضاً بالنظام الخطي. اما المتتابعة المتكونة من n من الأعداد الحقيقية sn،
… ، s2،
s1 = xn
حلاً لكل معادلة من النظام الخطي.
ويمكن كتابه النظام الخطي المتكون من m من المعادلات التي تحتوي
على n من المتغيرات بالصيغة:
a11x1 + a12x2 + … + a1m xn = c1
X21x1 + a22x2 + … + a2m xn = c2
… … …
am1 +am2 x2 + … + amn xn = cm
إذ أن xn ، … ، x2 ، x1 هي متغيرات و .... ، ...
ثوابت حيث:
1،2،…..،m i= ، j=1،2،….n
طريقة حل أنظمة المعادلات
الخطية
الطريقة الأساسية لحل نظام معادلات خطية تكون باستبدال نظام
معطى بنظام جديد يمتلك مجموعة الحل نفسها ولكن أسهل في الحل. يتم الحصول على هذا
النظام الجديد بسلسلة خطوات بتطبيق ثلاث أنواع من العمليات وذلك لحذف المجاهيل:
1- تبادل معادلتين لبعضهما الاخرى.
2- ضرب معادلة ما يثابت غير صفري.
3- جمع مضاعف إحدى المعادلات إلى أخرى.
ولكن كيف بإمكاننا إيجاد الحل باستخدام التمثيل البياني
نقوم
بتمثيل المعادلة الأولى ومن ثم تمثيل المعادلة الثانية
نقطة
التقاء تلك المستقيمات تعطي الحل لنظام المعادلات
وهذا ماتقوم به البرمجية
وكلما
غيرنا تمثيل تلك المستقيمات حسب النظام الموجود لدينا يتغير الحل ليعطي حل النظام
الجديد
فمثلاً لو
طلب منك إيجاد حل النظام التالي:
y=2x , y=4x+3
نقوم
بتمثيل المستقيم الأول الذي لا يقطع المحور y في أي نقطة لعدم وجود معامل ثابت للمعادلة و نختار نقطتين لتمثيل
الخط مثلاً النقطة (٠،٠) و النقطة (١،٢) ونقوم بتمثيله
وكذلك
المستقيم الآخر نختار نقطتين (٣،٠) ،
(٧،١)
ونمثلها
فتكون نتيجة تقاطع المستقيمين هي الحل للنظام كالتالي:
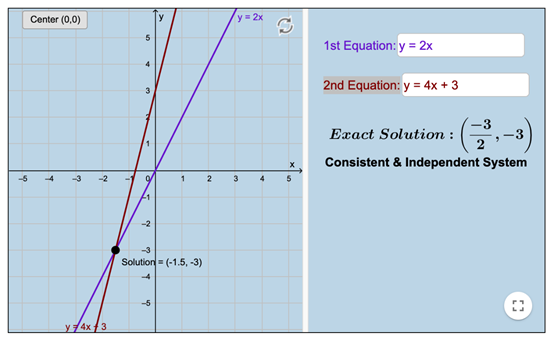
كما أنه بإمكاننا ادخال المعادلة يدوياً في البرمجية في الجزء الأعلى
باليمين كالتالي:
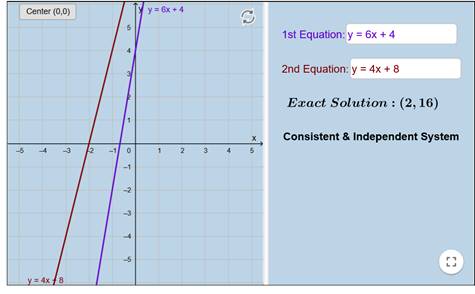
ليظهر لنا تمثيلهما بيانياً مع حل النظام أسفل الادخال يمين الشاشة
نقوم بادخل محاولة أخرى لمعادلتين خطيتين أخريتيين:
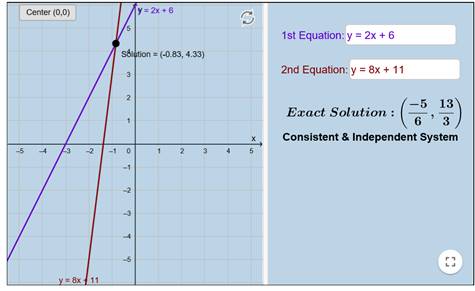
فنجد أن المعادلتين ترسمان بشكل مباشر مع إيجاد الحل للنظام أسفل
المعادلتين بجهة اليمين.
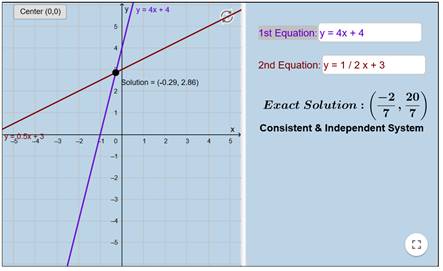
فمثلاً لو أردنا تمثيل المعادلتين
y = 4x + 4
y = 3x + 2
قم الآن بإدخال بيانات المعادلة في المستطيل الأول باللون الأبيض على
جهة اليمين
ندخل الآن بيانات المعادلة الثانية
y = 3x + 2
إدخالا يدوياً في المعادلة الثانية في المربع الثاني الأبيض كالتالي:
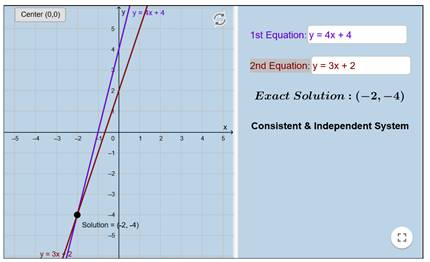
ونجد أن الحل يظهر أسفل المستطيلين و تمثيلها
يظهر على جهة اليسار