تمثيل المتباينات الخطية

رابط البرمجية

https://www.geogebra.org/m/dudJx9VE

الهدف من البرمجية

التأكد من عمليات رسم المتباينات الخطية

شرح رسم المتباينات الخطية

يتم رسم المتباينات الخطية بنفس الطريقة التي نقوم بها برسم المعادلة الخطية ولكن الاختلاف في تمثيل البيانات بعد رسم الخط المستقيم حسب إشارة المتباينة

فمثلاً إن كان لدينا المتباينة

6x+2y <1

نقوم بداية بتحويلها لمعدلة

6x+2y=1

نضع مجموعة من النقاط في جدول ونمثل الخط المستقيم

x	0	1\6
y	1\2	0

ونقوم بتمثيل النقطتين ورسم المستقيم الناتج

وحيث أن علامة المتباينة بدون علامة المساواة سيكون الخط متقطع

ولو كانت بعلامة المساواة سيكون الخط متصل

بعد أن نقوم برسمها نختار نقطة من النقاط في المستوى و نعوض عنها في معادلة المتباينة فإن حققته فإنها في منطقة الحل وإن لم تحققه فهذا يدل على أن الحل بالمنطقة الأخرى

مثلاً:

نختار النقطة (1،2)

نعوض عنها في المعادلة

6x+2y <1

6(2)+2(1) =14

بما أن

14 <1

إذن النقطة المختارة تحقق المعادلة

بالتالي تقع في منطقة الحل

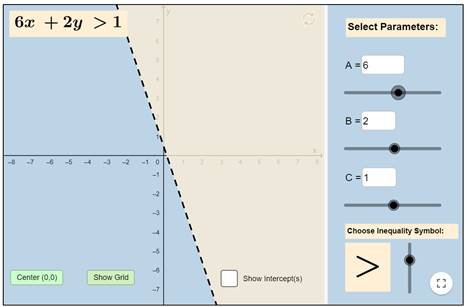
بالتالي منطقة الحل هي المنطقة المظللة باللون البيج.

شرح البرمجية الخاصة بالتحقق من رسم المتباينات الخطية

نقوم بإدخال معاملات المتباينة

Ax+By < C

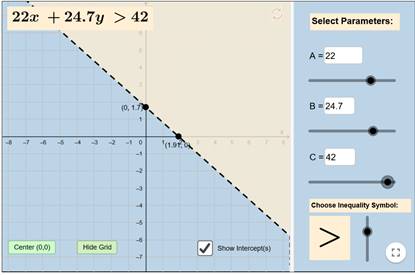
يتم وضع المعاملات في المنطقة المخصصة لذلك في المربعات البيضاء باليمين إما بالادخال اليدوي أو بتحريك النقطة السوداء تحت كل معامل من المعاملات

ويتم تغيير الإشارة الخاصة بالمتباينة من أسفل اليمين بتحريك النقطة السوداء على الخط للأعلى أو الأسفل وسيتم تمثيل المتباينة مباشرة على اليسار كالتالي:

التوضيح بالتفصيل:

قم بوضع معامل x في المربع الأول عن طريق تحريك النقطة السوداء الأولى بجانب حرف A

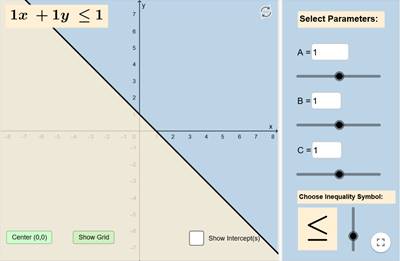
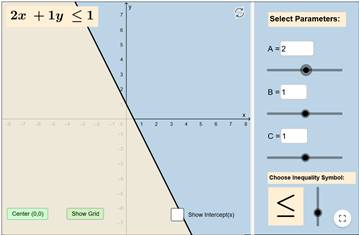
و الان غير قيمة معامل y من النقطة الثانية بجانب حرف B

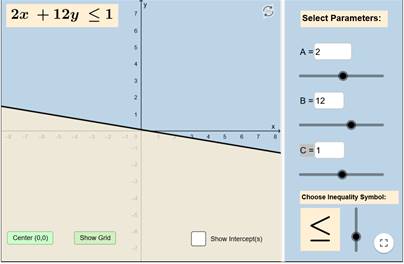
و الان غير قيمة المعامل الثابت من النقطة الثالثة بجانب حرف C

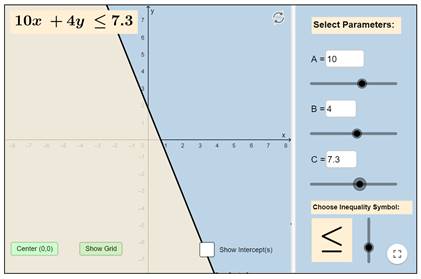
والان نقوم بتغيير الإشارة الخاصة بالمتباينة من اخر نقطة كالتالي

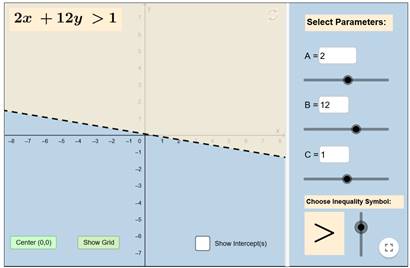
في حال أردنا إظهار الشبكة التربيعية نقوم بالضغط على أيقونة المربع الأخضر الأيمن بالأسفل لتظهر كالتالي:

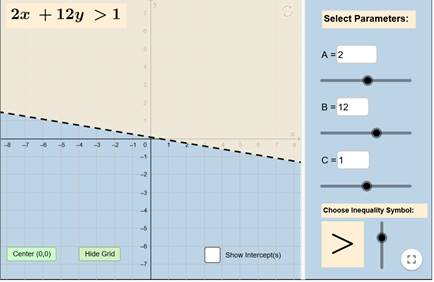
في حال رغبنا باظهار النقطتين المقطوعين من المحورين نقوم بالضغط على أيقونة المربع الأبيض بالأسفل لتظهر كالتالي