وتران متقاطعان في دائرة
Crossing Chords
https://aghandoura.com/A1/HANAN/APPLET/G2-28.html
الهدف من البرمجية:
التعرف على خصائص وتران متقاطعان في دائرة
الوتر: هو القطعة المستقيمة التي تصل بين نقطتين من نقط الدائرة
شرح البرمجية والخطوات التفصيلية
بعد الضغط على رابط البرمجية ستنتقل إلى الصفحة التالية:

آلية عمل البرمجية
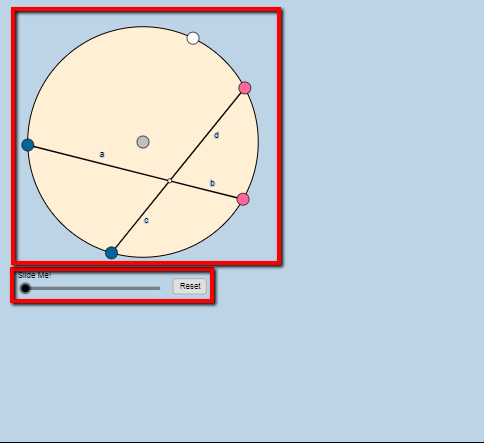
تتكون البرمجية من:
· دائرة مرسوم فيها وتران بنقاط يمكن تحريكها.
· مؤشر أسود للتحكم بالخصائص المراد التعرف عليها.
ثانياً: شرح الفكرة القائمة عليها البرمجية وخطوات العمل
تقوم فكرة البرمجية على التعرف على خصائص وتران متقاطعان في دائرة
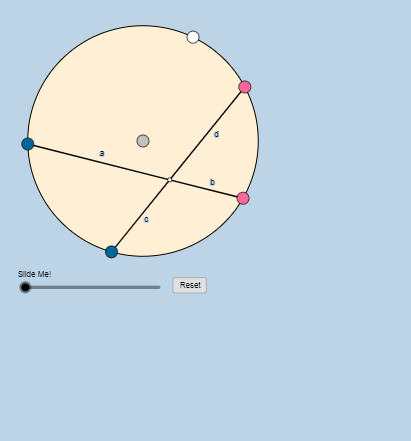
ابدأ بالنشاط:
قم بتحريك مركز الدائرة، ماذا تلاحظ؟
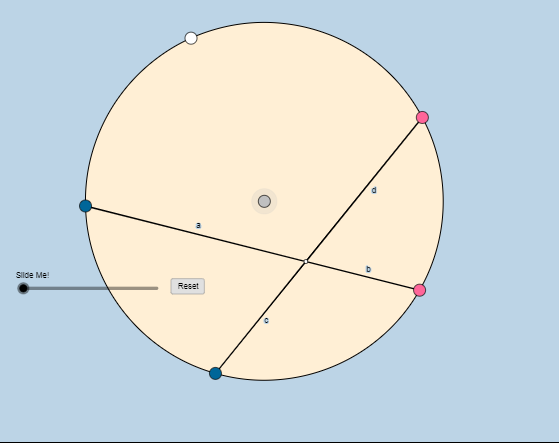
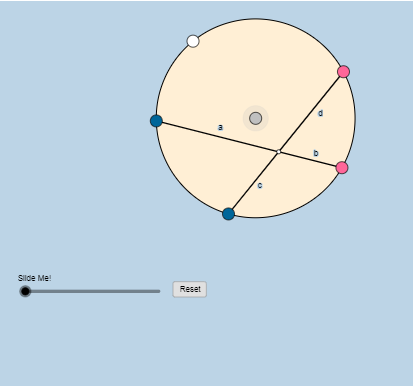
نلاحظ أن حجم الدائرة يتغير
قم بتحريك النقاط الواقعة على أطراف الدائرة، ماذا تلاحظ؟
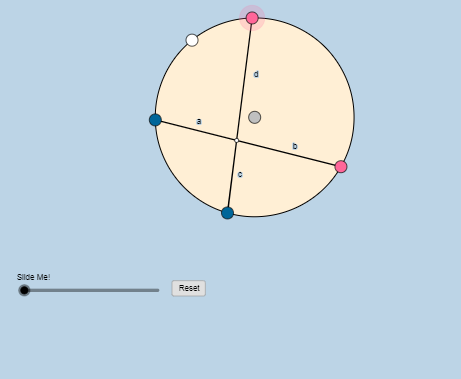
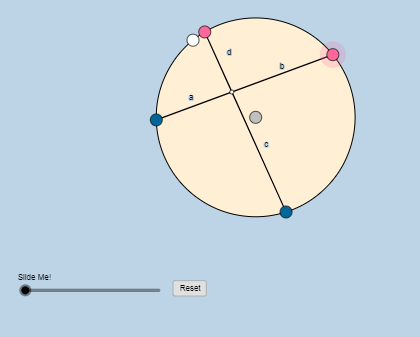

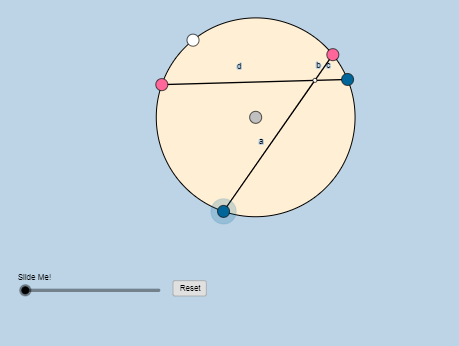
نلاحظ أن:
- نلاحظ أن طول الوتران ثابت
- ونلاحظ أن نقطة تقاطعهما تختلف
-
- وَتَرُ الدائرةِ هو: قطعة مستقيمة واصلةٌ بين نقطتين على الدائرة.
- يُسمّى أطولُ وترٍ في الدائرةِ قُطراً. بينما الخطُّ القاطع هو امتدادٌ لانهائيٌّ للوتر.
قم بتحريك المؤشر الأسود تدريجياً ماذا تلاحظ؟
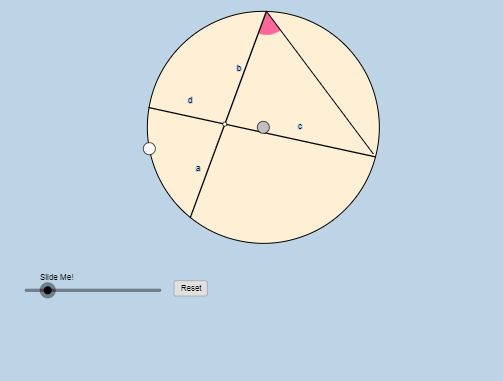
تم رسم مثلث وتحديد زاوية ما
قم بتحريك المؤشر الأسود تدريجياً ماذا تلاحظ؟
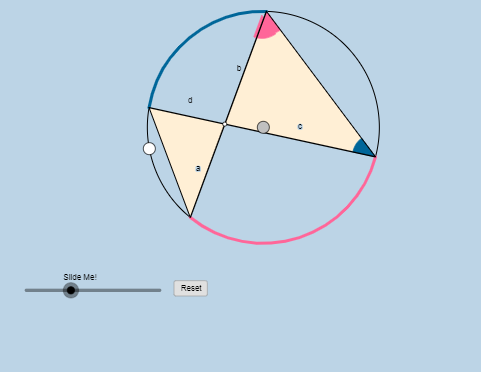
تم رسم مثلث اخر وتحديد أقواس في الدائرة
أي أن الوتر يقسم الدائرة الى قوسين
قم تحريك المؤشر الأسود قليلا، ماذا تلاحظ؟
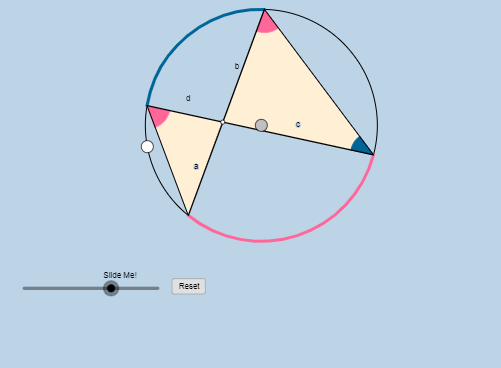
تم ملاحظ أن قياس الزاوية الوردية في المثلث الكبير يساوي قياس الزاوية في المثلث الصغير
قم تحريك المؤشر الأسود قليلا، ماذا تلاحظ؟
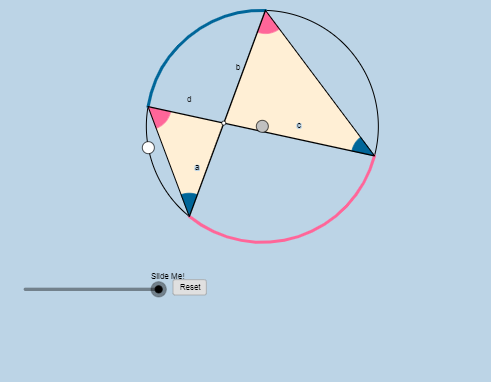
تم ملاحظ أن قياس الزاوية الزرقاء في المثلث الكبير يساوي قياس الزاوية في المثلث الصغير
قارن بين المثلثين، ماذا تستنتج؟
نلاحظ وجود أقواس بألوان الزوايا
أي أن قياس الزاوية الوردية تساوي نصف قياس الزاوية الزرقاء
أي أن قياس الزاوية المحصورة بين الوترين
أي أن
قياس الزاوية المحصورة بين وترين متقاطعين في دائرة يساوي نصف مجموع قياسي القوسين المقابلين لتلك الزاوية
قم بتكرار النشاط وسجل ملاحظات أخرى
إعداد / هيفاء سعد العتيبي