لوحة المكعبات الفرنسية:

بعد التعامل مع إحدى أهم الوسائل التعليمية الخاصة بالمكفوفين والتي لا يمكن أن يستغني عنها الكفيف وهي ما يعرف باسم لوحة المكعبات الفرنسية تم إدخال العديد من الاستخدامات التي لا تحتاج إلى لغة برايل . وفي ما يلي شرح موجز عن اللوحة وطريقة استخدامها بدون لغة برايل.

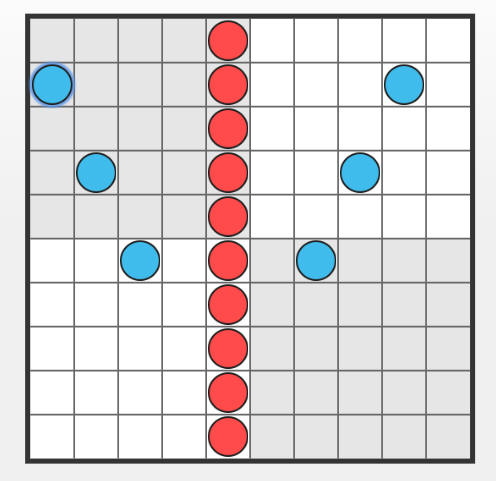
لوحة المكعبات الفرنسية:هي لوح مستطيل الشكل مصنوع من البلاستيك المقوّى مقسّم إلى مكعبات مفرّغة (عشرون مكعباً في أحد البعدين وخمسة عشر مكعباً في البعد الآخر) ويرافق هذا اللوح عدد من المكعبات الصغيرة التي يمكن إدخالها  داخل تلك المكعبات المجوّفة.ويُستخدم اللوح مع تلك المكعبات في إجراء العمليات الحسابية على الأعداد الصحيحة والنسبية وتحليل الأعداد, كما يستخدم في قراءة الأعداد من خلال الرموز المكتوبة بلغة برايل على كل وجه من أوجه تلك المكعبات الصغيرة.والشكل التالي  يوضح لوحة المكعبات الفرنسية قبل التعديل.

 لوحة المكعبات الفرنسية خالية من المكعبات

 وقد تمت الاستعانة بالمكعبات المتداخلة الصغيرة وهي إحدى اليدويات. وهذه المكعبات بلاستيكية بكل منها بروز على أحد الأوجه الستة للمكعب, في حين أن كل وجه من أوجه المكعب الباقية يوجد به ثقب يمكن لذلك البروز الموجود في أحد أوجه مكعب آخر أن يدخل فيه ليكّونا معاً مكعبين .وبهذه الطريقة يمكن بناء مكعب كبير من تلك المكعبات الصغيرة, كما يمكن بناء متوازي مستطيلات أيضاً مما يسهل على الكفيف إدراك مفهوم الحجم , وحساب حجم العديد من المجسمات من خلال عد المكعبات التي يتكون منها المجسم, فعدد المكعبات التي يتكون منها الجسم يمثل الحجم على اعتبار أن المكعب الصغير يمثل وحدة الحجم , وهذا هو المفهوم الرياضي للحجم .فحجم الجسم هو ببساطة عدد الوحدات المكعبة التي يتكون منها ذلك المجسم . اما دراسة المساحات فيمكن حسابها من خلال التعامل مع سطح اللوحة حيث كل نقطة تمثل البروز الموجود في أحد أوجه كل مكعب من المكعبات المتداخلة,هذا البروز يمكن للكفيف تلمسه وعد النقاط الموجودة على سطح اللوحة. فعدد النقاط(البروزات) يمثل مساحة السطح. وهذا هو المفهوم الرياضي للمساحة .فالمساحة هي ببساطة عدد الوحدات المربعة التي يتكون منها السطح.

 ويمكن استخدام هذه اللوحة في دراسة مساحة المربع ومساحة المستطيل من خلال عد النقاط .فالمستطيل الذي طوله10 سم وعرضه 8 سم يمكن تمثيله على اللوحة وحساب مساحته عدد النقاط(عدد المربعات).

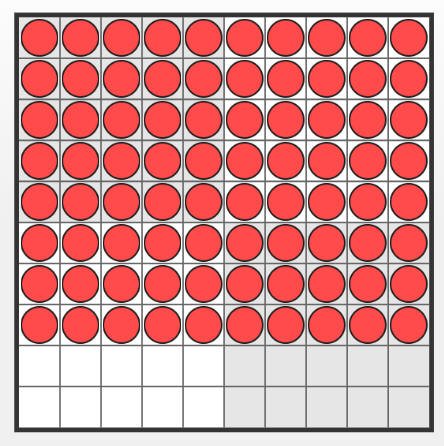
والشكل التالي يوضح لوحة المكعبات الفرنسية وقد تم تعبئتها بالمكعبات المتداخلة.وعددها يمثل مساحة اللوحة ,أي مساحة المستطيل الذي تمثله اللوحة  بمعنى أن المساحة=  15x 20 =  600 وحدة مربعة.

 

  لوحة المكعبات الفرنسية  10 في 10 تم تعبئتها بالمكعبات المتداخلة 

  الشكل التالي يوضح مساحة مستطيل أحد بعديه     10سم والآخر 8  سم. 

كما يمكن استخدام لوحة المكعبات الفرنسية مع المكعبات المتداخلة في دراسة العمليات على الكسور, فعند جمع كسرين يتم بناء مستطيل بعده الأول يساوي مقام الكسر الأول, وبعده الثاني يساوي مقام الكسر الثاني.فعند جمع ثلث + ربع يتم تكوين مستطيل 3X4 ثم حساب عدد النقاط التي تمثل ثلث هذا المستطيل (4 في هذه الحالة) وعدد النقاط التي تمثل الكسر الثاني(3 في هذه الحالة) مما يعني أن حاصل الجمع يساوي 7نقاط. وحيث إن النقطة الواحدة (المربع الواحد) في هذه الحالة تمثل جزءً من 12 جزءً (مجموع النقاط في المستطيل) يكون ناتج الجمع7/12

والشكل التالي يمثل جزءً من اللوحة يوضح عملية الجمع.

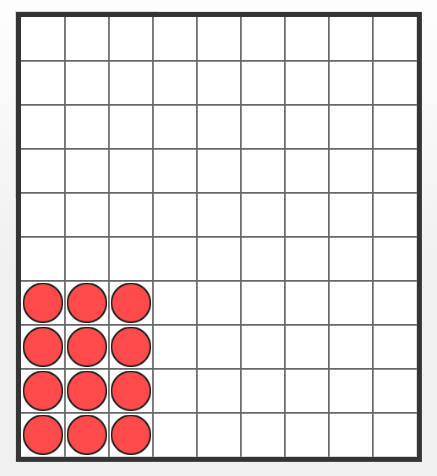
     وبالطريقة نفسها يمكن جمع أي كسرين وطرحهما.

كما يمكن تعليم الطالب الكفيف القسمة المنتهية والقسمة الإقليدية باللوحة نفسها فالشكل السابق من الممكن أن يكون تمثيلاً لقسمة 12 على 4 حيث يطلب المعلم تكوين مستطيل من العدد المقسوم (12في هذه الحالة) شريطة أن يكون أحد بعدي المستطيل هو العدد المقسوم عليه(4في هذه الحالة) ويكون خارج القسمة هو البعد الثاني للمستطيل (3 في هذه الحالة). وبالطريقة نفسها يمكن تمثيل القسمة غير المنتهية, فقسمة 30 على 4 مثلاً تتم بإعطاء الكفيف عدداَ من المكعبات يساوي العدد المقسوم(30في هذه الحالة) ثم نطلب منه تكوين مستطيل من كل المكعبات شريطة أن يكون أحد بعدي المستطيل يساوي العدد المقسوم عليه . بالتجربة يجد الكفيف أن بإمكانه بناء مستطيل من هذه المكعبات بعده الآخر يساوي 7 وهذا البعد يمثل خارج القسمة ويبقى معه مكعبان يمثلان الباقي .أي أن:

(المقسوم=المقسوم عليه Xخارج القسمة+ الباقي ) والشكل التالي يوضح الفكرة: 

 

 حيث المقسوم=30

والمقسوم عليه =4

خارج القسمة  =7

والباقي مكعبان اثنان

المقسوم = ( المقسوم عليه xخارج القسمة ) + الباقي

 كما يمكن استخدام اللوحة في شرح التناظر حول محور حيث يتم تعبئة  أي عمود من اللوحة بالمكعبات المتداخلة واعتباره محور التناظر على النحو التالي: 

 ويتم شرح التناظر بوضع مكعب على يمين الخط ويُطلب من الطالب وضع مكعب على يسار الخط شريطة أن يكون على استقامة المكعب الأول(في الصف نفسه) وعلى ذات البعد الذي يبعده المكعب الذي نريد الحصول على نظيره .والشكل التالي يوضح الفكرة: 

أما قواسم العدد فيمكن شرحها باستخدام لوحة المكعبات الفرنسية والمكعبات المتداخلة. فقواسم العدد 12 مثلاً يمكن إيجادها من خلال الخطوات التالية:

o       خذ عدداً من المكعبات يساوي العدد الذي تريد إيجاد قواسمه .

o       قم ببناء كافة المستطيلات الممكنة من كامل عدد المكعبات.

o       سجل بعدي كل مستطيل يتم تكوينه من كامل عدد المكعبات.

بهذه الطريقة يستطيع الكفيف إدراك مفهوم قواسم العدد. فقواسم العدد 20 يحصل عليها من بناء مستطيل بعداه  20,1  ومستطيل آخر بعداه 10,2 وثالث بعداه 5,4 ولا يمكنه بناء أي مستطيلات أخرى بغير تلك الأبعاد , مما يعني أن قواسم العدد 20 هي :

1’2’3’4

 وبالمثل فإن المستطيلات التي يمكن تكوينها من 18 مكعباً هي:

مستطيل بعداه 1’18 ومستطيل بعداه2’9 ومستطيل بعداه3’6 ولا يمكنه بناء مستطيلات أخرى مما يعني أن قواسم العدد 18 هي :

1’2’3’6’9’18 وبعد ذلك ينطلق في حساب قواسم أخرى فالعدد 36 قواسمه:

 (1’36) ,(2’18 ),( 3’12) ,( 4’9 ),( 6,6 )مما يعني أن قواسم العدد 36 هي : 1’2’3’4’6’9’18,12’36

وقواسم العدد بهذه الطريقة تمهد لدراسة القاسم المشترك الأكبر لعددين وذلك بترتيب قواسمهما وإيجاد القاسم المشترك الأكبر بيناهما , فالقاسم المشترك الأكبر للعددين  18 وَ 24  يمكن حسابه من خلال معرفة قواسم كل منهما.

قواسم العدد 18 هي : 1’2’9,6,3’18

قواسم العدد 24 هي : 1’2’3’6,4’24,12,8

  وحيث إن القواسم المشتركة للعددين  هي 1’2 ’3’6 وأكبرها هو العدد 6 فإن القاسم المشترك الأكبر للعددين  18’24 هو 6

ومن خلال التعرف على القاسم المشترك الأكبر يمكن إيجاد المضاعف المشترك الأصغر لهذين العددي بتطبيق القانون التالي :

القاسم المشترك الأكبر لعددين x المضاعف المشترك الأصغر = حاصل ضرب العددين 

المضاعف المشترك الأصغر=( حاصل ضرب  العددين  )على(القاسم المشترك الأكبر)

ليس هذا فحسب بل يمكن القول إن أكثر من 80% من رياضيات المرحلة الابتدائية  يمكن تدريسها بهذه اللوحة كما يمكن تدريس العديد من رياضيات المرحلة المتوسطة بها.