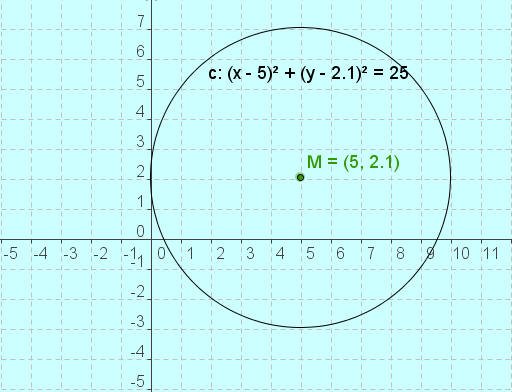
معادلة الدائرة
اضغط هنا لمشاهدة البرمجية
الهدف العام : استنتاج معادلة الدائرة بمعلومية مركزها وطول نصف قطرها
الأهداف التفصيلية:
تحديد إحداثيات مركز الدائرة على الشبكة التربيعية.
تحديد إحداثيات نقطة على سطح الدائرة على الشبكة التربيعية.
استخدام قانون طول القطعة المستقيمة في التوصل إلى معادلة الدائرة .
المادة العلمية: معادلة الدائرة التي مركزها ( M ) ونصف قطرها ( نق ) في المستوى ( ح × ح ) هي :( س - أ )2 + ( ص - ب )2 =نق2
شرح البرمجية:
النقطةتمثل مركز الدائرة وتأتي على صورة زوج مرتب تمثل الإحداثيين السيني والصادي لمركز الدائرة (M) ، يتم تحريك الدائرة بوضع المؤشر على أي نقطة على محيطها ووضعها في المكان المناسب حسب إحداثيات مركزها المطلوبة،وبالتالي تقوم البرمجيةبدورها بإيجاد معالة الدائرة مباشرة،لاحظ الشكل التالي:

مثال:
· لإيجاد معادلة الدائرة التي مركزها ( M ) ونصف قطرها ( نق ) في المستوى (ح × ح) نقوم بالخطوات التالية:
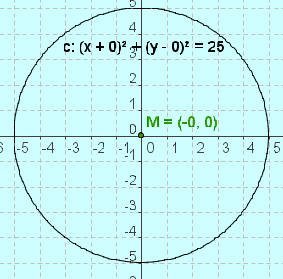
· نفترض أن إحداثيات المركز ( M ) في المستوى (ح × ح) هي ( أ ، ب )
وأن نقطة (H) التي تقع على محيط الدائرة إحداثياتها في المستوى (ح ×ح) هي (س ، ص)
· نطبق قانون طول قطعة مستقيمة على نصف القطر[ M H] نحصل على المعادلة ( س - أ )2 + ( ص - ب )2 =نق2 .
· وبتطبيق ذلك على الدائرة الموضحة بالرسم وبالتعويض عن إحداثيات المركز ( M ) في المستوى (ح × ح) بنقطة الأصل ( 0 ، 0 ) تصبح المعادلة الخاصة بالدائرة كالتالي : ( س - 0 )2 + ( ص - 0 )2 =نق2
· وبالتالي تكون معادلة الدائرة هي : س2 + ص2 = نق2